Что такое среднее арифметическое медиана

Что такое среднее арифметическое медиана

Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите рассчитать.

Среднее арифметическое, размах, мода и медиана

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.

Для ряда a₁,a₁. a_n среднее арифметическое вычисляется по формуле:

Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32

Модой ряда чисел называется число, которое встречается в данном ряду чаще других.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.

Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.

Медианой упорядоченного ряда чисел с нечётным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.

Примеры

Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды ряда.

Источник

Медиана в статистике

Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.

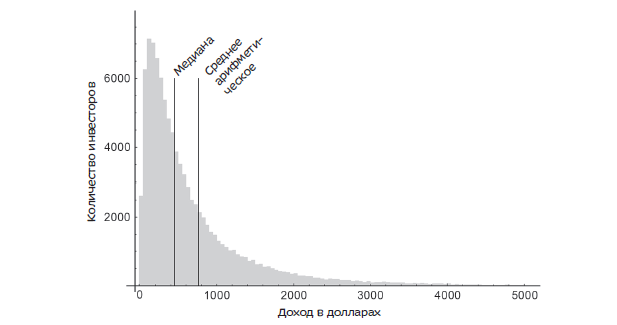
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.

Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.

Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.

Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).

Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).

Формула медианы

Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.

Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:

№_Me – номер значения, соответствующего медиане,

N – количество значений в совокупности данных.

Тогда медиана обозначается, как

Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:

В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.

Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.

Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.

Обратимся к наглядной схеме.

Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:

где x_Me — нижняя граница медианного интервала;

i_Me — ширина медианного интервала;

∑f/2 — количество всех значений, деленное на 2 (два);

S_(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;

f_Me — число наблюдений в медианном интервале.

Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.

Для примера рассчитаем медиану по следующим данным.

Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.

По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.

То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.

Расчет медианы в Excel

Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.

Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:

Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.

Ниже видеоролик о том, как рассчитать медиану в Excel.

Источник

Среднее против медианы

Значит (или средний) и медиана статистические термины, которые играют в чем-то похожую роль с точки зрения понимания основная тенденция набора статистических оценок. Хотя среднее значение традиционно

Содержание:

Значит (или средний) и медиана статистические термины, которые играют в чем-то похожую роль с точки зрения понимания основная тенденция набора статистических оценок. Хотя среднее значение традиционно было популярной мерой средней точки в выборке, у него есть недостаток, заключающийся в том, что любое отдельное значение оказывается слишком высоким или слишком низким по сравнению с остальной частью выборки. Вот почему медиана иногда используется как лучший показатель средней точки.

Сравнительная таблица

Определения среднего и медианы

Как рассчитать

В Значит или среднее, вероятно, наиболее часто используемый метод описания центральной тенденции. Среднее значение вычисляется путем сложения всех значений и деления полученной оценки на количество значений. В среднее арифметическое образца

представляет собой сумму значений выборки, деленную на количество элементов в выборке:

пример

Сравнение среднего, медианы и моды двух логнормальных распределений с разной асимметрией.

Недостатки средних арифметических и медиан

Среднее значение не является надежным статистическим инструментом, поскольку его нельзя применить ко всем распределениям, но оно является наиболее широко используемым статистическим инструментом для определения центральной тенденции. Причина, по которой это среднее значение не может применяться ко всем распределениям, заключается в том, что на него чрезмерно влияют значения в выборке, которые слишком малы или слишком велики.

Недостаток медианы в том, что с ней трудно справиться теоретически. Нет простой математической формулы для вычисления медианы.

Другие виды средств

Есть много способов определить центральную тенденцию или среднее значение набора ценностей. Рассмотренное выше среднее технически является средним арифметическим и является наиболее часто используемой статистической величиной для среднего. Есть и другие виды средств:

Среднее геометрическое

Среднее геометрическое определяется как п-й корень продукта п числа, т.е. для набора чисел Икс₁,Икс₂. Икс_п, среднее геометрическое определяется как

Средние геометрические параметры лучше, чем средние арифметические, для описания пропорционального роста. Например, хорошим приложением для вычисления среднего геометрического является расчет совокупного годового темпа роста (CAGR).

Гармоническое Среднее

Пифагорейские средние

Среднее арифметическое, среднее геометрическое и среднее гармоническое вместе образуют набор средних, называемых пифагорейскими средними. Для любого набора чисел гармоническое среднее всегда является наименьшим из всех пифагоровых средних, а среднее арифметическое всегда является наибольшим из трех средних. Т.е. среднее гармоническое ≤ среднее геометрическое ≤ среднее арифметическое.

Другие значения слов

Источник

Среднее арифметическое, мода и медиана

Предмет, цели и методы математической статистики

Начиная с XVIII века, в общем направлении статистических исследований начинает активно формироваться математическая статистика.

Математическая статистика – раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.

В зависимости от предмета исследований математическая статистика делится на:

В зависимости от цели и методов исследований математическая статистика делится на: описательную статистику; теорию оценивания; теорию проверки гипотез.

1. Наглядное представление в форме графиков и таблиц.

2. Количественное описание с помощью статистических показателей.

1. Параметрические методы (наименьших квадратов, максимального правдоподобия и др.).

2. Непараметрические методы.

1. Последовательный анализ.

2. Статистические критерии.

Метод выборочных исследований

Статистика получила признание в различных областях человеческой деятельности благодаря заметной экономии времени и прочих ресурсов. Её основная идея: не нужно измерять всё, измерьте только часть всего и сделайте предположение об остальном.

«Всё» в статистике называется генеральной совокупностью.

«Часть всего», которую мы тщательно исследуем, называется выборкой.

Метод выборочных исследований – способ определения свойств группы объектов ( генеральной совокупности ) на основании статистического исследования её части ( выборки ).

Например, чтобы оценить средние размеры апельсина, который продаётся в магазине в декабре, необязательно денно и нощно мерить все апельсины во всех ящиках (сколько же для этого нужно времени и людей?!). Достаточно сделать выборку – мерить по одному апельсину из каждого ящика в течение месяца (тут уже и один человек справится).

Статистика предоставляет методику и оценки для того, чтобы правильно провести выборку и на основании знаний о среднем размере апельсина в выборке (выборочной средней) судить о средних размерах всех декабрьских апельсин (генеральной средней).

Средняя арифметическая, простая и взвешенная

Статистическое исследование опирается на собранные данные о каком-то признаке (рост, вес, возраст, доход и т.п.).

Варианта – полученное эмпирическое значение признака.

Вариационный ряд – совокупность собранных вариант.

Пусть мы сделали выборку, провели N измерений и получили x_1,x_2,…,x_N вариант.

Чтобы найти выборочную среднюю дискретного вариационного ряда, нужно вычислить среднюю арифметическую простую :

На протяжении четверти школьник получил такие оценки по алгебре: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4. Найдите среднюю оценку за четверть.

Считаем среднюю арифметическую простую:

Нетрудно заметить, что оценки повторяются, и вычисления можно упростить, если вместо сложения одинаковых оценок использовать умножение оценок на их количество.

Чтобы найти выборочную среднюю при повторяющихся вариантах, удобно вычислять среднюю арифметическую взвешенную:

Рассматриваем тот же ряд оценок: 5,4,3,5,4,4,5,4,3,5,5,4,3,5,4,4 и составляем таблицу:

Источник

«Средние» значения — ваш враг. Как не попасться на удочку усреднения

СМИ, политика и бизнес часто оперируют данными о среднем: средний доход, средняя продолжительность жизни, средний потребитель. Иногда эти цифры полезны, но часто — бессмысленны и даже обманчивы. Автор книги «Путеводитель по лжи» Дэниел Левитин рассказывает, как не попасться на удочку усреднения.

Среднее арифметическое, медиана и мода

Есть три вида средних, и они могут выражаться разными числами. Поэтому те, кто всерьез занимается статистикой, избегают слова «среднее», отдавая предпочтение более точным терминам: среднее арифметическое, медиана или мода. Иногда все эти величины совпадают, но чаще они различаются.

Чаще других встречается среднее арифметическое; оно равно сумме всех данных, поделенной на их количество. Медиана — это число в середине упорядоченного набора чисел (статистики называют его выборкой): половина данных находится ниже этого значения, а половина выше. Мода — цифра, которая встречается чаще других.

Бимодальное распределение

Если вы работаете со средними, остерегайтесь бимодального распределения. Во многих наборах данных — биологических, физических, социальных — у распределения может быть два или больше пиков.

Например, подобный график может отображать сумму, потраченную на обеды в неделю (ось X), и количество людей, потративших такую сумму (ось Y). Представьте, что вы изучали две группы людей: детей (левый горб) — они покупают школьные обеды — и руководителей компаний (правый горб) — они ходят в дорогие рестораны.

Среднее арифметическое и медиана в данном случае — это числа где-то между этими двумя горбами, и они ничего не скажут о том, что происходит на самом деле, — ведь во многих случаях среднее арифметическое и медиана отражают ту сумму, которую никто не тратит. Подобный график говорит лишь о том, что в вашем примере имеет место неоднородность — вы сравниваете яблоки с апельсинами. В таком случае лучше сразу сказать, что вы имеете дело с бимодальным распределением, и сообщить о двух модах. А еще лучше разделить группу на две подгруппы и собрать статистические данные для каждой.

Экологическая ошибка

Будьте осторожны, когда будете делать выводы об отдельных людях и о группах, основываясь на средних данных. Тут легко наткнуться на экологическую ошибку.

Экологическую ошибку совершают те, кто считает, что если выбрать наугад человека из группы с более высоким средним доходом, то и у него доход будет выше.

Средний инвестор не получает средний доход

Посещает ли средний студент колледжа колледж среднего размера, растет ли среднее дерево в среднем лесу и получает ли средний инвестор средний доход? Нет.

В одном исследовании средний доход от инвестиции 100 долларов на срок 30 лет составил 760 долларов, или 7% в год. Звучит неплохо. Но эта статистика не показывает, что 9% инвесторов потеряли деньги, а огромному числу инвесторов, 69%, не удалось достигнуть показателя среднего дохода. Так случилось потому, что среднее арифметическое было смещено из-за нескольких человек, заработавших больше среднего.

Будьте осторожны со средними, а также с тем, как их интерпретируют. Усредняя данные по выборкам из несопоставимых совокупностей, игнорируя разброс значений, допуская экологические ошибки мы видим мир искаженным и принимаем неверные решения.

Источник

• ← Что такое слот для ci pcmcia
• Что такое сиалор аква →