Что такое среднее арифметическое взвешенное

8.3. Средние величины в статистике

Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).

Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.

Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.

Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенно­стей, присущих отдельным единицам.

ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:

Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.

ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН

Таблица 8.2 – Результаты опроса работников офиса

Источник

Как вычислить среднее арифметическое взвешенное

Среднее арифметическое — это статистический показатель, иллюстрирующий среднее значение набора данных, который рассчитывается как сумма всех значений, деленная на их количество. Это важный коэффициент, получивший широкое распространение в прикладных науках.

Что такое среднее арифметическое

Суть данного показателя проще всего продемонстрировать на примере. Торговец продает на рынке яблоки. В понедельник ему удалось продать 54 кг, во вторник — 47 кг, а в среду — 61 кг. Торговец хочет спланировать свои продажи и ему интересно, сколько килограмм фруктов он продает в среднем за день. Вот здесь на сцену и выходит среднее арифметическое. Для его определения необходимо суммировать значения показателей и разделить на их количество.

Среднее = (54 + 47 + 61) / 3 = 54 кг

Торговец выяснил, что в среднем он продает 54 кг яблок в день и может грамотно спрогнозировать свои затраты на покупку товара. Так как килограмм яблок стоит 10 рублей, то в день наш коммерсант зарабатывает в среднем 540 рублей.

Среднее арифметическое широко используется в статистике в случаях, если рассматривается набор однородных данных. В нашем случае это были только яблоки. Однако если торговец расширит свой ассортимент и добавит на прилавки еще и апельсины? Как изменится средняя стоимость одной единицы товара?

Пусть в понедельник торговец реализовал 23 кг апельсинов, во вторник — 28 кг, а в среду — 21 кг. Средний уровень продаж апельсинов составит:

Среднее = (28 + 21 + 23) / 3 = 24 кг.

Так как цена одного килограмма цитрусов составляет 20 рублей, то средний доход от продажи апельсинов составит 480 рублей в день.

Теперь решим простую на первый взгляд задачу. Какова средняя стоимость реализации одного килограмма любого товара? Неискушенный аналитик решит эту задачу как:

Среднее = (20 + 10) / 2 = 15 рублей,

за килограмм апельсинов или яблок. Однако не все так просто. В случае с разнородными данными важно учитывать их вес.

Среднее арифметическое взвешенное

Данный показатель используется при расчете среднего арифметического для разных данных, каждое из которых имеет свой вес. Для определения взвешенного параметра необходимо каждое значение умножить на свой вес, суммировать эти произведения, после чего разделить на сумму весов.

В данном случае у нас есть средний вес каждого вида фруктов и его необходимо учесть для определения средней цены одного килограмма товара. На практике это выглядит так:

Среднее взвешенное = (20 × 24 + 10 × 54) / (24 + 54) = 13,07.

Естественно, 13,07 не сильно отличается от 15, однако чем больше слагаемых и больший разброс весов, тем сильнее отличается среднее взвешенное от простого среднего арифметического. Также очевидно, что если все веса равны единице, то среднее взвешенное становится равным среднему арифметическому.

Что выбрать?

Если требуется найти среднее значение одного элемента из однородного набора, то достаточно отыскать среднее арифметическое. Именно это мы делали при поиске среднего уровня продажи яблок или апельсинов за день. Если требуется найти среднее между разными элементами, принадлежащими к разным группам или отыскать среднее средних, то для расчета используется среднее арифметическое взвешенное.

Наша программа представляет собой калькулятор для расчета среднего арифметического и его взвешенного варианта. В меню калькулятора вы можете выбрать тип искомого параметра. Для расчета среднего арифметического вам понадобится ввести только значения параметров. В случае необходимости вы можете добавить дополнительные ячейки.

Для расчета взвешенного среднего выберите соответствующий пункт в меню калькулятора, укажите значения и их вес. Рассмотрим на примерах, как рассчитывать взвешенное значение.

Примеры из реальной жизни

Подсчет средней зарплаты

Пусть на вашем предприятии числятся сотрудники, каждый из которых получает зарплату в соответчики с должностью. Для рекламного проспекта о поиске персонала вы хотите уточнить, на какую среднюю зарплату может рассчитывать соискатель. Вы знаете, что:

Для вычисления средней зарплаты на предприятии вам потребуется ввести в ячейки значений размер зарплаты, а в ячейки весов — количество сотрудников, которые ее получают. Калькулятор мгновенно выдаст вам результат, что средняя зарплата равна 19 540 рублей. Без учета веса значений среднее арифметическое было бы равно 22 666 рублей, что уже значительно отличается от взвешенного значения.

Средняя скорость автомобиля

Допустим, водитель ехал по городскому проспекту со скоростью 60 км/ч в течение одного часа. Затем он выехал на автомагистраль, увеличил скорость до 120 км/ч и ехал так три часа, после чего свернул на проселочную дорогу и со скоростью 40 км/ч ехал еще два часа. С какой средней скоростью ехал водитель? В этой задаче в качестве веса выступает время езды, а значений — скорость. Выглядит это так:

Введем эти данные в форму калькулятора и получим ответ: средняя скорость автомобиля составляет 83,3 км/ч. Без учета времени средняя скорость была бы равна 73,3 км/ч, что неверно.

Заключение

Расчет среднего арифметического взвешенного широко используется в прикладных науках. Этот параметр популярен не только в статистике, но и в физике, экономике или финансах. Используйте наши калькуляторы в качестве помощника для решения практических и теоретических задач.

Источник

Средняя взвешенная

Средняя арифметическая взвешенная применяется в том случае, когда отдельные значения признака (варианты) встречаются в ряду распределения не с одинаковой частотой (f ₁ ≠ f ₂ ≠ …f _n ) и число вариантов не совпадает с частотой их появления.

Пример расчета:

При расчете средней арифметической по интервальному вариационному ряду необходимо сначала найти середину интервалов. Это и будут значения x_i, а количество единиц совокупности в каждой группе f _i. При наличии открытого интервала, его ш ирина принимается равной ширине примыкающего (рядом стоящего) интервала.

Стаж работника, лет

Число работников, чел.

Середина интервала, лет

1. Средний стаж работников предприятия определяется по средней арифметической взвешенной. Он будет равен:

2. Размах вариации R=Хmax-Хmin зависит только от двух крайних значений признака: R =11-1=10(лет).

3. Взвешенное среднее линейное отклонение (средний модуль) является средней величиной из абсолютных значений отклонений индивидуальных значений признака от общей средней арифметической величины:

4. Взвешенное среднее квадратическое отклонение определяется как квадратный корень из дисперсии. На столько, в среднем, отклоняется средний стаж работников предприятия по каждой группе от общей средней (среднего стажа по предприятию).

5. Коэффициент вариации характеризует колеблемость признака около средней. Если коэффициент вариации не превышает 33%, то совокупность, по рассматриваемому признаку, можно считать однородной. Данная совокупность характеризуется сильной вариацией, т.е. разброс значений по отдельным группам относительно общего среднего стажа по предприятию значителен.

Источник

В средневзвешенное арифметическое похож на обычный среднее арифметическое (самый распространенный вид средний), за исключением того, что вместо того, чтобы каждая из точек данных вносила равный вклад в окончательное среднее значение, некоторые точки данных вносили больший вклад, чем другие. Понятие взвешенного среднего играет роль в описательная статистика а также встречается в более общей форме в нескольких других областях математики.

Если все веса равны, то средневзвешенное значение совпадает с среднее арифметическое. В то время как взвешенные средние обычно ведут себя аналогично средним арифметическим, у них действительно есть несколько нелогичных свойств, как, например, зафиксировано в Парадокс Симпсона.

Содержание

Примеры

Базовый пример

Учитывая два школьных класса, один с 20 учениками и один с 30 учениками, оценки в каждом классе по тесту были:

Или это может быть достигнуто путем взвешивания средних значений класса по количеству учеников в каждом классе. Большему классу придается больший «вес»:

Икс ¯ = ( 20 × 80 ) + ( 30 × 90 ) 20 + 30 = 86. < displaystyle < bar > = < frac <(20 times 80) + (30 times 90)><20 + 30>> = 86.>

Таким образом, средневзвешенное значение позволяет найти среднюю оценку учащегося, не зная оценки каждого учащегося. Требуются только средства класса и количество учеников в каждом классе.

Пример выпуклой комбинации

Поскольку только относительный веса имеют значение, любое средневзвешенное значение может быть выражено с помощью коэффициентов, которые в сумме равны единице. Такая линейная комбинация называется выпуклое сочетание.

Используя предыдущий пример, мы получили бы следующие веса:

Затем примените такие веса:

Икс ¯ = ( 0.4 × 80 ) + ( 0.6 × 90 ) = 86. < displaystyle < bar > = (0,4 times 80) + (0,6 times 90) = 86.>

Математическое определение

который расширяется до:

Следовательно, элементы данных с высоким весом вносят больший вклад в средневзвешенное значение, чем элементы с низким весом. Вес не может быть отрицательным. Некоторые из них могут быть равны нулю, но не все (поскольку деление на ноль недопустимо).

Тогда для таких нормализованных весов средневзвешенное значение будет:

Икс ¯ = ∑ я = 1 п ш я ′ Икс я < displaystyle < bar > = sum _ ^ ‘x_ >> .

Обратите внимание, что всегда можно нормализовать веса, сделав следующее преобразование исходных весов:

Использование нормализованного веса дает те же результаты, что и при использовании исходных весов:

В стандартная ошибка среднего взвешенного (отклонения затрат на единицу), σ Икс ¯ < displaystyle sigma _ < bar >> может быть показано через распространение неопределенности быть:

σ Икс ¯ = ( ∑ я = 1 п ш я ) − 1 < displaystyle sigma _ < bar > = left ( < sqrt < sum _ ^ >>> right) ^ <- 1>>

Статистические свойства

Средневзвешенное значение выборки, Икс ¯ < displaystyle < bar >> , сама по себе является случайной величиной. Его ожидаемое значение и стандартное отклонение связаны с ожидаемыми значениями и стандартными отклонениями наблюдений следующим образом. Для простоты мы предполагаем нормализованные веса (веса, суммирующие единицу).

Если наблюдения имеют ожидаемые значения

тогда средневзвешенное значение выборки имеет ожидание

σ Икс ¯ 2 = ∑ я = 1 п ш я ′ 2 σ я 2 < displaystyle sigma _ < bar > ^ <2>= sum _ ^ ‘^ <2>sigma _ ^ <2>>>

чей квадратный корень σ Икс ¯ < displaystyle sigma _ < bar >> можно назвать стандартная ошибка средневзвешенного значения (общий случай). [ нужна цитата ]

Веса дисперсии

Средневзвешенное значение в этом случае:

и стандартная ошибка средневзвешенного значения (с весами дисперсии) является:

Приведенные выше уравнения можно объединить для получения:

Значение этого выбора в том, что это средневзвешенное значение является оценщик максимального правдоподобия среднего вероятностных распределений в предположении, что они независимы и нормально распределенный с тем же средним.

Корректировка чрезмерной или недостаточной дисперсии

Взвешенные средние обычно используются для нахождения взвешенного среднего исторических данных, а не теоретически сгенерированных данных. В этом случае будет некоторая ошибка в дисперсии каждой точки данных. Обычно экспериментальные ошибки могут быть недооценены из-за того, что экспериментатор не принимает во внимание все источники ошибок при вычислении дисперсии каждой точки данных. В этом случае необходимо скорректировать дисперсию средневзвешенного значения, чтобы учесть тот факт, что χ 2 < displaystyle chi ^ <2>> слишком большой. Исправление, которое необходимо сделать, это

σ ^ Икс ¯ 2 = σ Икс ¯ 2 χ ν 2 < displaystyle < hat < sigma>> _ < bar > ^ <2>= sigma _ < bar > ^ <2>chi _ < nu>^ <2>>

Квадратный корень σ ^ Икс ¯ < displaystyle < hat < sigma>> _ < bar >> можно назвать стандартная ошибка средневзвешенного значения (веса дисперсии, скорректированная шкала).

Проверка загрузки

Это было показано самонастройка методы, которые являются точной оценкой квадрата стандартной ошибки среднего (общий случай): [1]

σ Икс ¯ 2 = п ( п − 1 ) ш s 2 [ ∑ ( ш я Икс я − ш s Икс ¯ ) 2 − 2 Икс ¯ ∑ ( ш я − ш s ) ( ш я Икс я − ш s Икс ¯ ) + Икс ¯ 2 ∑ ( ш я − ш s ) 2 ] < displaystyle sigma _ < bar > ^ <2>= < frac <(n-1) w_ ^ <2>>> left [ sum (w_ x_ -w_ < bar >) ^ <2>-2 < bar > sum (w_ -w_ ) (w_ x_ < i>-w_ < bar >) + < bar > ^ <2>sum (w_ -w_ ) ^ <2>right]>

σ Икс ¯ 2 = п ( п − 1 ) ш s 2 ∑ ш я 2 ( Икс я − Икс ¯ ) 2 < displaystyle sigma _ < bar > ^ <2>= < frac <(n-1) w_ ^ <2>>> sum w_ ^ <2>(x_ — < bar >) ^ <2>>

Взвешенная дисперсия выборки

Обычно при вычислении среднего значения важно знать отклонение и стандартное отклонение о том, что имею ввиду. Когда взвешенное среднее μ ∗ < Displaystyle mu ^ <*>> , дисперсия взвешенной выборки отличается от дисперсии невзвешенной выборки.

В пристрастный взвешенный выборочная дисперсия σ ^ ш 2 < Displaystyle < шляпа < sigma>> _ < mathrm > ^ <2>> определяется аналогично нормальному пристрастный выборочная дисперсия σ ^ 2 < Displaystyle < шляпа < sigma>> ^ <2>> :

Частотные веса

Это эффективно применяет поправку Бесселя для частотных весов.

Если частотные веса < ш я > < displaystyle >> нормализованы к 1, то правильное выражение после поправки Бесселя становится

Обратите внимание, что оценка может быть несмещенной, только если веса не стандартизированный ни нормализованный, эти процессы изменяют среднее значение и дисперсию данных и, таким образом, приводят к потеря базовой ставки (подсчет населения, необходимый для поправки Бесселя).

Весы надежности

Окончательная объективная оценка дисперсии выборки:

В качестве дополнительного примечания были описаны другие подходы для вычисления взвешенной дисперсии выборки. [3]

Ковариация взвешенной выборки

А матрица взвешенной ковариации имеет вид: [4]

Как и в случае взвешенной выборочной дисперсии, существуют две разные несмещенные оценки в зависимости от типа весов.

Частотные веса

Если веса частотные веса, то беспристрастный взвешенная оценка ковариационной матрицы C < displaystyle textstyle mathbf > , с поправкой Бесселя, определяется как: [4]

Обратите внимание, что эта оценка может быть несмещенной, только если веса не стандартизированный ни нормализованный, эти процессы изменяют среднее значение и дисперсию данных и, таким образом, приводят к потеря базовой ставки (подсчет населения, необходимый для поправки Бесселя).

Весы надежности

В случае веса надежности, веса нормализованный:

(Если это не так, разделите веса на их сумму для нормализации перед вычислением V 1 < displaystyle V_ <1>> :

и беспристрастный взвешенная оценка ковариационной матрицы C < displaystyle textstyle mathbf > является: [5]

Рассуждения здесь те же, что и в предыдущем разделе.

Векторнозначные оценки

Сказанное легко обобщается на случай усреднения векторных оценок. Например, оценки положения на самолете могут иметь меньшую уверенность в одном направлении, чем в другом. Как и в скалярном случае, средневзвешенное значение нескольких оценок может дать максимальная вероятность оценивать. Мы просто заменяем дисперсию σ 2 < displaystyle sigma ^ <2>> посредством ковариационная матрица C < displaystyle mathbf > и арифметический обратный посредством матрица обратная (оба обозначаются одинаково, через верхний индекс); матрица весов будет выглядеть так: [6]

Средневзвешенное значение в этом случае:

(где порядок матрично-векторное произведение не является коммутативный) в терминах ковариации взвешенного среднего:

Например, рассмотрим средневзвешенное значение точки [1 0] с высокой дисперсией во втором компоненте и [0 1] с высокой дисперсией в первом компоненте. потом

тогда средневзвешенное значение:

что имеет смысл: оценка [1 0] «совместима» во втором компоненте, а оценка [0 1] согласована в первом компоненте, поэтому взвешенное среднее почти равно [1 1].

Учет корреляций

Снижение силы взаимодействия

Экспоненциально убывающие веса

Средневзвешенные функции

Понятие средневзвешенного значения можно распространить на функции. [7] Средневзвешенные функции играют важную роль в системах взвешенного дифференциального и интегрального исчисления. [8]

Источник

Средневзвешенное значение — формула в Excel

В одной из предыдущих статей мы обсудили три основные функции для вычисления среднего в Excel, которые очень просты и просты в использовании.

Но что, если некоторые значения более важны, чем другие, и, следовательно, вносят больший вклад в конечное среднее значение? Например, если вы участвуете в экзаменах и все экзамены имеют одинаковый вес, они одинаково важны, то для вас важно именно среднее значение оценки.

Однако в реальной жизни это не всегда так. Например, если вы изучаете программирование, то насколько важны для вас оценки по истории и физкультуре по сравнению с оценками по профильным дисциплинам?

Некоторые задачи всегда важнее других. Некоторые экзамены важнее других.

В таких ситуациях вам как раз и необходимо рассчитывать средневзвешенное значение.

Хотя Microsoft Excel не предоставляет специальной функции взвешенного среднего, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что показано в следующих примерах.

Что такое средневзвешенное значение?

Оно является своего рода средним арифметическим, в котором некоторые элементы набора данных имеют большую значимость, чем другие. Другими словами, каждому исходному показателю присваивается определенный вес.

В математике и статистике вы вычисляете взвешенное среднее значение, умножая каждое число в наборе на его вес, затем складываете произведения и делите итог сложения произведений на сумму всех весомостей.

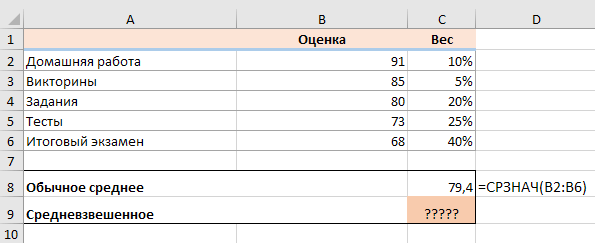
В этом примере, чтобы посчитать средневзвешенную итоговую оценку, вы умножаете каждый полученный балл на соответствующий процент (преобразованный в десятичную дробь), складываете эти 5 произведений вместе и делите это число на итог сложения пяти весов:

((91 * 0,1) + (85 * 0,05) + (80 * 0,2) + (73 * 0,25) + (68 * 0,4)) / (0,1 + 0,05 + 0,2 + 0,25 + 0,4) = 74,8

Формулы для средневзвешенного значения в Excel

В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.

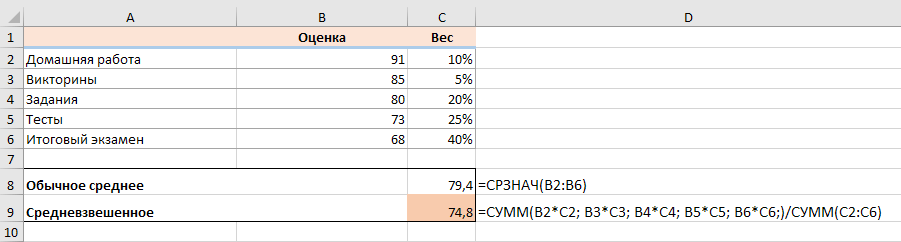
Пример 1. Функция СУММ.

По сути, он выполняет те же вычисления, что и описанные выше, за исключением того, что вы предоставляете ссылки на ячейки вместо чисел.

Посмотрите на рисунок чуть ниже: формула возвращает точно такой же результат, что и вычисления, которые мы делали минуту назад. Обратите внимание на разницу между нормальным средним, возвращаемым при помощи СРЗНАЧ в C8, и средневзвешенным (C9).

Несмотря на то, что формула эта очень проста и понятна, но она не подходит, если вы хотите усреднить большое количество элементов. Ведь придётся перечислять множество аргументов, что довольно утомительно.

В этом случае вам лучше использовать функцию СУММПРОИЗВ (SUMPRODUCT в английской версии). Об этом – ниже.

Пример 2. Функция СУММПРОИЗВ

Она идеально подходит для нашей задачи, так как предназначена для сложения произведений чисел. А это именно то, что нам нужно.

Таким образом, вместо умножения каждого числа на показатель его значимости по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом контексте массив представляет собой непрерывный диапазон ячеек), а затем делите результат на итог сложения весов:

= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )

Итак, формула умножает 1- е число в массиве 1 на 1- е в массиве 2 (в данном примере 91 * 0,1), а затем перемножает 2- е число в массиве 1 на 2- е в массиве 2 (85 * 0,15). в этом примере) и так далее. Когда все умножения выполнены, Эксель складывает произведения. Затем делим полученное на итог весов.

Чтобы убедиться, что функция СУММПРОИЗВ дает правильный результат, сравните ее с формулой СУММ из предыдущего примера, и вы увидите, что числа идентичны.

В нашем случае сложение весов дает 100%. То есть, это просто процент от итога. В таком случае верный результат может быть получен также следующими способами:

Но при использовании функции СУММ или СУММПРОИЗВ веса совершенно не обязательно должны составлять 100%. Однако, они также не должны быть обязательно выражены в процентах.

Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:

Видите, в этом случае мы обошлись без процентов.

Пример 3. Средневзвешенная цена.

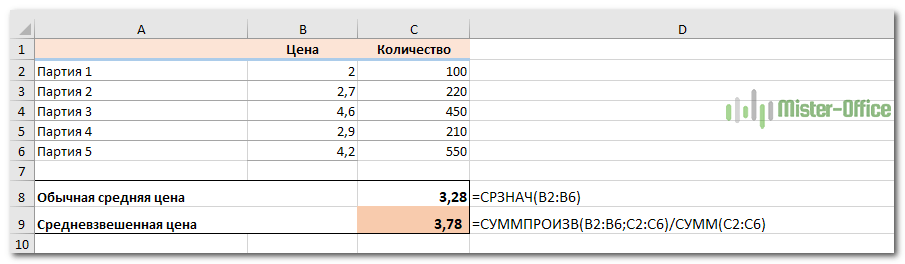
Еще одна достаточно часто встречающаяся проблема – как рассчитать средневзвешенную цену товара. Предположим, мы получили 5 партий товара от различных поставщиков. Мы будем продавать его по одной единой цене. Но чтобы ее определить, нужно знать среднюю цену закупки. В тот здесь нам и пригодится расчет средневзвешенной цены. Взгляните на этот простой пример. Думаю, вам все понятно.

Итак, средневзвешенная цена значительно отличается от обычной средней. На это повлияли 2 больших партии товара по высокой цене. А формулу применяем такую же, как и при расчете любого взвешенного среднего. Перемножаем цену на количество, складываем эти произведения, а затем делим на общее количество товара.

Ну, это все о формуле средневзвешенного значения в Excel.

Источник