Что такое среднее геометрическое чисел

Среднее геометрическое

Предлагаемая здесь программа, помимо расчета среднего геометрического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию.

Среднее геометрическое или среднее пропорциональное используется человечеством в архитектурных, землемерных и инженерных расчетах не менее 2500 лет. Об этом достоверно известно благодаря математическому трактату Евклида «Начала».
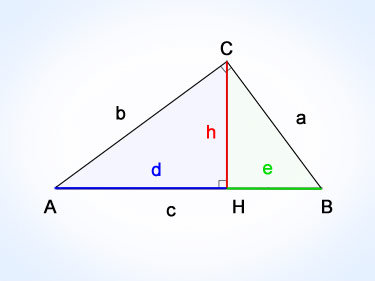
В своей второй теореме Евклид доказывает, что в прямоугольном треугольнике высота проведенная из прямого угла (рисунок) делит противоположную сторону так что:

Собственно говоря, благодаря второй теореме Евклида среднее геометрическое и получило свое название. В древнем мире математики ограничивалось только использованием корня квадратного (геометрия) и корня кубического (стереометрия).
Вообще говоря, извлечение корня с различными целыми показателями является частным случаем дробной степени. Но к такому пониманию этих алгебраических операции математики подошли только в семнадцатом веке. Неоценимый вклад в достижении обобщенного понимания степенных алгебраических операции внес Рене Декарт.

В свете современных представлений:

Среднее геометрическое значение множества положительных вещественных чисел определяется как результат взаимного умножения этих чисел и извлечения из произведения корня с показателем равным количеству чисел:

Таким образом, мы имеем дело исключительно с положительными вещественными числами и находим такое число, что при замене каждого из этих чисел их произведение не изменяется.

Расчет среднего геометрического

Введите исходные данные

Что-то пошло не так. Прямое восхождение не может быть больше 24 часов, минуты и секунды больше 60, а склонение по абсолютной величине не должно быть больше 90°

Среднее геометрическое, a_{ср. геом}

Для наглядной демонстрации правила о средних

выводим так же результат расчета среднего арифметического:

Среднее арифметическое [1] , a_{ср. арифм}

Design by Sergey Ov for abc2home.ru

ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:

Сохранить расчет среднего геометрического в истории браузера

Адресную строку с кодом из Ваших данных Вы можете переслать на любое устройство и воспроизвести на нем результаты расчетов

После того как будут введены хотя бы два исходных числа, цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый, и автоматически начнется расчет среднего геометрического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.

Страницы по теме «Расчет средних значений»

Свойства среднего геометрического

1. Среднее геометрическое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.

2. Кроме того среднее геометрическое подчиняется неравенству о средних для множества положительных вещественных чисел

то есть для любого множества положительных чисел среднее геометрическое никогда не бывает больше среднего арифметического [1] :

Прикладное значение среднего геометрического

P.S. На этой странице используется Бета версия программы расчета среднего геометрического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).

1. Среднее арифметическое значение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:

2. Среднее степенное значение s_d порядка (степени) d от множества заданных чисел a ₁ + a ₂ + …+ a _n определяется формулой:

Источник

Среднее геометрическое чисел

В данной публикации мы рассмотрим, с помощью какой формулы можно найти среднее геометрическое чисел, а также разберем примеры задач для ее демонстрации на практике.

Расчет среднего геометрического

Чтобы вычислить среднее геометрическое двух или более чисел, требуется их перемножить, а затем из полученного результата извлечь корень, степень которого равняется их количеству.

Частные случаи формулы:

» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Количество чисел	Формула
2	» data-order=»«>
3	» data-order=»«>
4	» data-order=»«>

Пример задачи

Задание 1
Найдем среднее геометрическое чисел 3, 6 и 12.

Решение:
Воспользуемся соответствующей формулой для трех чисел:

Задание 2
Среднее геометрическое четырех чисел равняется 4, а также известны три из них – 2, 2 и 4. Найдем четвертое.

Помещаем число 4 под знак корня, сохранив равенство (для этого возводим его в четвертую степень, т.е. ):

Источник

Среднее геометрическое чисел – формула и примеры

Средние величины в статистике дают обобщающую характеристику анализируемого явления. Самая распространенная из них – среднее арифметическое. Она применяется, когда агрегатный показатель образуется с помощью суммы элементов. Например, масса нескольких яблок, суммарная выручка за каждый день продаж и т.д. Но так бывает не всегда. Иногда агрегатный показатель образуется не в результате суммирования, а в результате умножения.

Такой пример. Месячная инфляция – это изменение уровня цен одного месяца по сравнению с предыдущим. Если известны показатели инфляции за каждый месяц, то как получить годовое значение? С точки зрения статистики – это цепной индекс, поэтому правильный ответ: с помощью перемножения месячных показателей инфляции. То есть общий показатель инфляции – это не сумма, а произведение. А как теперь узнать среднюю инфляцию за месяц, если имеется годовое значение? Нет, не разделить на 12, а извлечь корень 12-й степени (степень зависит от количества множителей). В общем случае среднее геометрическое рассчитывается по формуле:

То есть корень из произведения исходных данных, где степень определяется количеством множителей. Например, среднее геометрическое двух чисел – это квадратный корень из их произведения

Среднее геометрическое трех чисел – кубический корень из произведения

и т.д.

Если каждое исходное число заменить на их среднее геометрическое, то произведение даст тот же результат.

Чтобы лучше разобраться, чем отличаются среднее арифметическое и среднее геометрическое, рассмотрим следующий рисунок. Имеется прямоугольный треугольник, вписанный в круг.

Из прямого угла опущена медиана a (на середину гипотенузы). Также из прямого угла опущена высота b, которая в точке P делит гипотенузу на две части m и n. Т.к. гипотенуза – это диаметр описанного круга, а медиана – радиус, то очевидно, что длина медианы a – это среднее арифметическое из m и n.

Рассчитаем, чему равна высота b. В силу подобия треугольников АВP и BCP справедливо равенство

Значит, высота прямоугольного треугольника – это среднее геометрическое из отрезков, на которые она разбивает гипотенузу. Такое наглядное отличие.

В MS Excel среднюю геометрическую можно найти с помощью функции СРГЕОМ.

Все очень просто: вызвали функцию, указали диапазон и готово.

На практике этот показатель используют не так часто, как среднее арифметическое, но все же встречается. Например, есть такой индекс развития человеческого потенциала, с помощью которого сравнивают уровень жизни в разных странах. Он рассчитывается, как среднее геометрическое из нескольких индексов.

Ниже видео, как найти среднее геометрическое чисел в Excel.

Источник

Среднее геометрическое часто используется для набора чисел, значения которых предназначены для перемножения или являются экспоненциальными по своей природе, например набор цифр роста: значения человеческого населения или процентные ставки финансовых вложений с течением времени.

СОДЕРЖАНИЕ

Расчет

Итерационные средства

Среднее геометрическое также является средним арифметически-гармоническим в том смысле, что если определены две последовательности ( ) и ( ): а п <\ textstyle a_ > час п <\ textstyle h_ >

В этом легко убедиться из того факта, что последовательности сходятся к общему пределу (что можно показать с помощью теоремы Больцано – Вейерштрасса ) и того факта, что среднее геометрическое сохраняется:

Замена арифметического и гармонического среднего парой обобщенных средних противоположных конечных показателей дает тот же результат.

Связь с логарифмами

Среднее геометрическое также может быть выражено как экспонента среднего арифметического логарифмов. Используя логарифмические тождества для преобразования формулы, умножения можно выразить как сумму, а степень как умножение:

тогда как среднее арифметическое является минимизатором

Таким образом, среднее геометрическое представляет собой сводку выборок, показатель степени которых лучше всего соответствует показателям степени образцов (в смысле наименьших квадратов).

Сравнение со средним арифметическим

Средняя скорость роста

Применение к нормированным значениям

Это делает среднее геометрическое единственно правильным средним при усреднении нормализованных результатов; то есть результаты, которые представлены как отношения к контрольным значениям. Это имеет место при представлении производительности компьютера по сравнению с эталонным компьютером или при вычислении единого среднего индекса из нескольких разнородных источников (например, ожидаемая продолжительность жизни, годы образования и младенческая смертность). В этом сценарии использование среднего арифметического или гармонического приведет к изменению ранжирования результатов в зависимости от того, что используется в качестве эталона. Например, возьмем следующее сравнение времени выполнения компьютерных программ:

Средние арифметические и геометрические «согласны», что компьютер C самый быстрый. Однако, представляя соответствующим образом нормализованные значения и используя среднее арифметическое, мы можем показать, что любой из двух других компьютеров является самым быстрым. Нормализация по результату A дает A как самый быстрый компьютер согласно среднему арифметическому:

в то время как нормализация по результату B дает B как самый быстрый компьютер согласно среднему арифметическому, но A как самый быстрый согласно среднему гармоническому:

и нормализация на результат C дает C как самый быстрый компьютер согласно среднему арифметическому, но A как самый быстрый согласно среднему гармоническому:

Во всех случаях рейтинг, определяемый средним геометрическим, остается таким же, как и рейтинг, полученный с ненормализованными значениями.

Однако это рассуждение было поставлено под сомнение. Давать стабильные результаты не всегда равносильно получению правильных результатов. Как правило, более строго назначать веса каждой из программ, вычислять средневзвешенное время выполнения (используя среднее арифметическое), а затем нормализовать этот результат на одном из компьютеров. В трех приведенных выше таблицах просто присваивается разный вес каждой из программ, объясняя несовместимые результаты средних арифметических и гармонических (первая таблица дает одинаковый вес обеим программам, вторая дает вес 1/1000 второй программе, а третий дает вес 1/100 второй программе и 1/10 первой). По возможности следует избегать использования среднего геометрического для агрегирования показателей производительности, потому что умножение времени выполнения не имеет физического смысла, в отличие от сложения времени, как в среднем арифметическом. Показатели, обратно пропорциональные времени (ускорение, IPC ), следует усреднять с использованием гармонического среднего.

Среднее геометрическое непрерывной функции

Приложения

Пропорциональный рост

Среднее геометрическое более подходит, чем среднее арифметическое, для описания пропорционального роста, как экспоненциального роста (постоянный пропорциональный рост), так и переменного роста; в бизнесе среднее геометрическое значение темпов роста известно как совокупный годовой темп роста (CAGR). Среднее геометрическое значение роста за периоды дает эквивалентную постоянную скорость роста, которая дает такую ​​же конечную сумму.

Предположим, апельсиновое дерево дает 100 апельсинов в год, а затем 180, 210 и 300 в последующие годы, поэтому рост составит 80%, 16,6666% и 42,8571% за каждый год соответственно. Используя среднее арифметическое, вычисляется (линейный) средний рост 46,5079% (80% + 16,6666% + 42,8571%, эта сумма затем делится на 3). Однако, если мы начнем со 100 апельсинов и позволим им расти на 46,5079% каждый год, в результате получится 314 апельсинов, а не 300, поэтому линейное среднее значение превышает годовой рост.

Вместо этого мы можем использовать среднее геометрическое. Рост с 80% соответствует умножению с 1.80, поэтому мы возьмем среднее геометрическое 1,80, 1.166666 и 1.428571, то есть ; таким образом, «средний» рост в год составляет 44,2249%. Если мы начнем со 100 апельсинов и позволим их количеству расти на 44,2249% каждый год, в результате получится 300 апельсинов. 1,80 × 1,166666 × 1,428571 3 ≈ 1,442249 <\ displaystyle <\ sqrt [<3>] <1,80 \ times 1.166666 \ times 1.428571>> \ приблизительно 1.442249>

Финансовый

Среднее геометрическое время от времени использовалось для расчета финансовых показателей (усреднение проводится по компонентам индекса). Например, в прошлом индекс FT 30 использовал среднее геометрическое. Он также используется в недавно введенном показателе инфляции RPIJ в Соединенном Королевстве и в Европейском Союзе.

Это приводит к занижению динамики индекса по сравнению с использованием среднего арифметического.

Приложения в социальных науках

Хотя среднее геометрическое используется относительно редко при вычислении социальной статистики, начиная с 2010 года Индекс человеческого развития Организации Объединенных Наций действительно перешел на этот способ расчета на том основании, что он лучше отражает незаменимый характер собираемых и сравниваемых статистических данных:

Среднее геометрическое снижает уровень взаимозаменяемости между [сравниваемыми] измерениями и в то же время гарантирует, что снижение предполагаемой продолжительности жизни при рождении на 1 процент оказывает такое же влияние на ИЧР, как снижение уровня образования или дохода на 1 процент. Таким образом, в качестве основы для сравнения достижений этот метод также более уважительно относится к внутренним различиям по измерениям, чем к простому среднему.

Равномерно распределенный доход, эквивалентный благосостоянию, связанный с индексом Аткинсона с параметром неприятия неравенства, равным 1,0, является просто геометрическим средним доходом. Для значений, отличных от единицы, эквивалентное значение представляет собой норму Lp, деленную на количество элементов, где p равно единице минус параметр неприятия неравенства.

Геометрия

Соотношения сторон

Среднее геометрическое использовалось при выборе компромиссного соотношения сторон в фильмах и видео: учитывая два соотношения сторон, их среднее геометрическое обеспечивает компромисс между ними, искажая или обрезая оба в некотором смысле одинаково. Конкретно, два прямоугольника равной площади (с одинаковым центром и параллельными сторонами) с разными соотношениями сторон пересекаются в прямоугольнике, соотношение сторон которого является средним геометрическим, а их корпус (наименьший прямоугольник, который содержит оба из них) также имеет соотношение сторон их среднее геометрическое.

Спектральная плоскостность

Антибликовые покрытия

Субтрактивное смешение цветов

Источник

Среднее геометрическое

Средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось. Более формально:

Содержание

Свойства

Среднее геометрическое взвешенное

Среднее геометрическое взвешенное набора вещественных чисел с вещественными весами определяется как

В том случае, если все веса равны между собой, среднее геометрическое взвешенное равно среднему геометрическому.

В геометрии

Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу, а каждый катет есть среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.

Это даёт геометрический способ построения среднего геометрического двух (длин) отрезков: нужно построить окружность на сумме этих двух отрезков как на диаметре, тогда высота, восставленная из точки их соединения до пересечения с окружностью, даст искомую величину.

Обобщения

См. также

Примечания

Статистические показатели
Описательная статистика	Непрерывные данные Коэффициент сдвига Среднее (Арифметическое, Геометрическое, Гармоническое) · Медиана · Мода · Размах Вариация Ранг · Среднеквадратическое отклонение · Коэффициент вариации · Квантиль (Дециль, Процентиль/Перцентиль/Центиль) Моменты Математическое ожидание · Дисперсия · Асимметрия · Эксцесс Дискретные данные Частота · Таблица контингентности
Статистический вывод и проверка гипотез	Статистический вывод Доверительный интервал (Частотная вероятность) · Достоверный интервал (Байесовский вывод) · Статистическая значимость · Мета-анализ Планирование эксперимента Генеральная совокупность · Планирование выборки · Районированная выборка · Репликация · Группировка · Чувствительность и специфичность Объём выборки Статистическая мощность · Мера эффекта · Стандартная ошибка Общая оценка Байесовская оценка решения · Метод максимального правдоподобия · Метод моментов нахождения оценок · Оценка минимального расстояния · Оценка максимального интервала Статистические критерии Z-тест · t-критерий Стьюдента · Критерий Фишера · Критерий Пирсона (Хи-квадрат) · Тест Вальда · U-критерий Манна — Уитни · Критерий Уилкоксона · Критерий Краскела — Уоллиса · Критерий Кохрена · Критерий Лиллиефорса Анализ выживания Функция выживания · Оценка Каплана — Мейера · Логранк-тест · Интенсивность отказов · Пропорциональная модель опасностей
Корреляция	Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания
Линейные модели	Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ
Регрессия	Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия

Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами

Полезное

Смотреть что такое «Среднее геометрическое» в других словарях:

СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ — (gеomеtric mean) Корень N й степени из произведения членов множества N, состоящего из x1, x2. хN Среднее геометрическое записывается как (Пiхi)1/N. Среднее геометрическое определено только для случаев, когда все хi – положительные числа.… … Экономический словарь

СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ — (geometric mean) Величина, равная корню n й степени из произведения n данных величин. Например, средним геометрическим от 7, 100 и 107 будет = 42,15, что значительно меньше, чем их среднее арифметическое (arithmetic mean), равное 71,3. Бизнес.… … Словарь бизнес-терминов

СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ — (geometric mean) Величина, равная корню n й степени из произведения и данных величин. Например, средним геометрическим от 7, 100, и 107 будет 3√74 900) = 42,15, что значительно меньше, чем их среднее арифметическое (arithmetic mean), равное 71,3 … Финансовый словарь

среднее геометрическое — geometrinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas n ąja šaknimi iš matuojamojo dydžio n verčių sandaugos. atitikmenys: angl. geometric average; geometric mean; geometrical mean vok. geometrisches … Penkiakalbis aiškinamasis metrologijos terminų žodynas

среднее геометрическое — geometrinis vidurkis statusas T sritis fizika atitikmenys: angl. geometric average; geometric mean; geometrical mean vok. geometrisches Mittel, n rus. среднегеометрическое значение, n; среднее геометрическое, n pranc. moyenne géométrique, f … Fizikos terminų žodynas

СРЕДНЕЕ, ГЕОМЕТРИЧЕСКОЕ — Измерение центральной тенденции для набора из n значений, представленное как n корень из произведения n значений. Используется не так часто, как среднее арифметическое, наибольшее применение оно находит в изучении средней скорости изменений.… … Толковый словарь по психологии

Среднее геометрическое взвешенное — набора вещественных чисел с вещественными весами определяется как В том случае, если все веса равны между собой, среднее геометрическое взвешенное равно среднему геометрическому. См. также Среднее геометрическое … Википедия

среднее геометрическое значение — geometrinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas n ąja šaknimi iš matuojamojo dydžio n verčių sandaugos. atitikmenys: angl. geometric average; geometric mean; geometrical mean vok. geometrisches … Penkiakalbis aiškinamasis metrologijos terminų žodynas

ГЕОМЕТРИЧЕСКОЕ СРЕДНЕЕ — ГЕОМЕТРИЧЕСКОЕ СРЕДНЕЕ, среднее геометрическое чисел n это n ый корень произведений данных чисел. Например, квадратный корень из произведений двух чисел 8 и 2 есть среднее геометрическое 8 и 2, равное Ц(832)=4. Среднее геометрическое 5, 8 и 25… … Научно-технический энциклопедический словарь

Источник