Что такое среднее взвешенное
Средневзвешенное значение — формула в Excel
В одной из предыдущих статей мы обсудили три основные функции для вычисления среднего в Excel, которые очень просты и просты в использовании.
Но что, если некоторые значения более важны, чем другие, и, следовательно, вносят больший вклад в конечное среднее значение? Например, если вы участвуете в экзаменах и все экзамены имеют одинаковый вес, они одинаково важны, то для вас важно именно среднее значение оценки.
Однако в реальной жизни это не всегда так. Например, если вы изучаете программирование, то насколько важны для вас оценки по истории и физкультуре по сравнению с оценками по профильным дисциплинам?
Некоторые задачи всегда важнее других. Некоторые экзамены важнее других.
В таких ситуациях вам как раз и необходимо рассчитывать средневзвешенное значение.
Хотя Microsoft Excel не предоставляет специальной функции взвешенного среднего, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что показано в следующих примерах.
Что такое средневзвешенное значение?
Оно является своего рода средним арифметическим, в котором некоторые элементы набора данных имеют большую значимость, чем другие. Другими словами, каждому исходному показателю присваивается определенный вес.
В математике и статистике вы вычисляете взвешенное среднее значение, умножая каждое число в наборе на его вес, затем складываете произведения и делите итог сложения произведений на сумму всех весомостей.
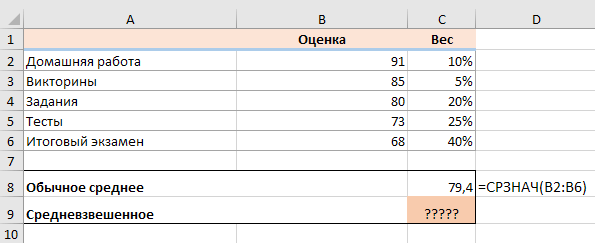
В этом примере, чтобы посчитать средневзвешенную итоговую оценку, вы умножаете каждый полученный балл на соответствующий процент (преобразованный в десятичную дробь), складываете эти 5 произведений вместе и делите это число на итог сложения пяти весов:
((91 * 0,1) + (85 * 0,05) + (80 * 0,2) + (73 * 0,25) + (68 * 0,4)) / (0,1 + 0,05 + 0,2 + 0,25 + 0,4) = 74,8
Формулы для средневзвешенного значения в Excel
В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.
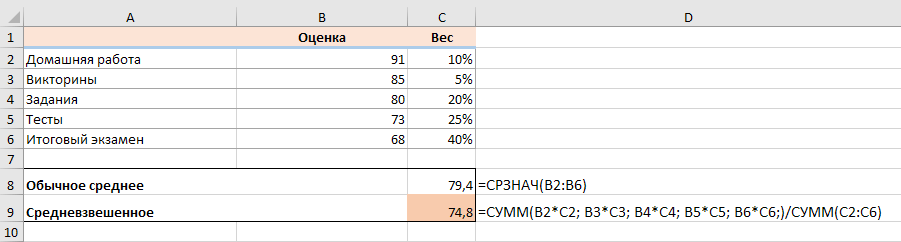
Пример 1. Функция СУММ.
По сути, он выполняет те же вычисления, что и описанные выше, за исключением того, что вы предоставляете ссылки на ячейки вместо чисел.
Посмотрите на рисунок чуть ниже: формула возвращает точно такой же результат, что и вычисления, которые мы делали минуту назад. Обратите внимание на разницу между нормальным средним, возвращаемым при помощи СРЗНАЧ в C8, и средневзвешенным (C9).
Несмотря на то, что формула эта очень проста и понятна, но она не подходит, если вы хотите усреднить большое количество элементов. Ведь придётся перечислять множество аргументов, что довольно утомительно.
В этом случае вам лучше использовать функцию СУММПРОИЗВ (SUMPRODUCT в английской версии). Об этом – ниже.
Пример 2. Функция СУММПРОИЗВ
Она идеально подходит для нашей задачи, так как предназначена для сложения произведений чисел. А это именно то, что нам нужно.
Таким образом, вместо умножения каждого числа на показатель его значимости по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом контексте массив представляет собой непрерывный диапазон ячеек), а затем делите результат на итог сложения весов:
= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )
Итак, формула умножает 1- е число в массиве 1 на 1- е в массиве 2 (в данном примере 91 * 0,1), а затем перемножает 2- е число в массиве 1 на 2- е в массиве 2 (85 * 0,15). в этом примере) и так далее. Когда все умножения выполнены, Эксель складывает произведения. Затем делим полученное на итог весов.
Чтобы убедиться, что функция СУММПРОИЗВ дает правильный результат, сравните ее с формулой СУММ из предыдущего примера, и вы увидите, что числа идентичны.
В нашем случае сложение весов дает 100%. То есть, это просто процент от итога. В таком случае верный результат может быть получен также следующими способами:
Но при использовании функции СУММ или СУММПРОИЗВ веса совершенно не обязательно должны составлять 100%. Однако, они также не должны быть обязательно выражены в процентах.
Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:
Видите, в этом случае мы обошлись без процентов.
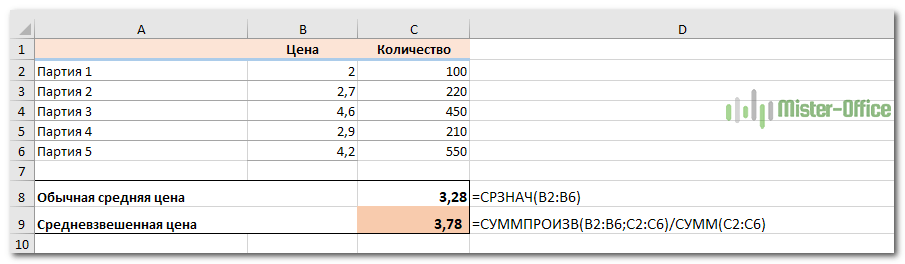
Пример 3. Средневзвешенная цена.
Еще одна достаточно часто встречающаяся проблема – как рассчитать средневзвешенную цену товара. Предположим, мы получили 5 партий товара от различных поставщиков. Мы будем продавать его по одной единой цене. Но чтобы ее определить, нужно знать среднюю цену закупки. В тот здесь нам и пригодится расчет средневзвешенной цены. Взгляните на этот простой пример. Думаю, вам все понятно.
Итак, средневзвешенная цена значительно отличается от обычной средней. На это повлияли 2 больших партии товара по высокой цене. А формулу применяем такую же, как и при расчете любого взвешенного среднего. Перемножаем цену на количество, складываем эти произведения, а затем делим на общее количество товара.
Ну, это все о формуле средневзвешенного значения в Excel.
Как вычислить среднее арифметическое взвешенное
Среднее арифметическое — это статистический показатель, иллюстрирующий среднее значение набора данных, который рассчитывается как сумма всех значений, деленная на их количество. Это важный коэффициент, получивший широкое распространение в прикладных науках.
Что такое среднее арифметическое
Суть данного показателя проще всего продемонстрировать на примере. Торговец продает на рынке яблоки. В понедельник ему удалось продать 54 кг, во вторник — 47 кг, а в среду — 61 кг. Торговец хочет спланировать свои продажи и ему интересно, сколько килограмм фруктов он продает в среднем за день. Вот здесь на сцену и выходит среднее арифметическое. Для его определения необходимо суммировать значения показателей и разделить на их количество.
Среднее = (54 + 47 + 61) / 3 = 54 кг
Торговец выяснил, что в среднем он продает 54 кг яблок в день и может грамотно спрогнозировать свои затраты на покупку товара. Так как килограмм яблок стоит 10 рублей, то в день наш коммерсант зарабатывает в среднем 540 рублей.
Среднее арифметическое широко используется в статистике в случаях, если рассматривается набор однородных данных. В нашем случае это были только яблоки. Однако если торговец расширит свой ассортимент и добавит на прилавки еще и апельсины? Как изменится средняя стоимость одной единицы товара?
Пусть в понедельник торговец реализовал 23 кг апельсинов, во вторник — 28 кг, а в среду — 21 кг. Средний уровень продаж апельсинов составит:
Среднее = (28 + 21 + 23) / 3 = 24 кг.
Так как цена одного килограмма цитрусов составляет 20 рублей, то средний доход от продажи апельсинов составит 480 рублей в день.
Теперь решим простую на первый взгляд задачу. Какова средняя стоимость реализации одного килограмма любого товара? Неискушенный аналитик решит эту задачу как:
Среднее = (20 + 10) / 2 = 15 рублей,
за килограмм апельсинов или яблок. Однако не все так просто. В случае с разнородными данными важно учитывать их вес.
Среднее арифметическое взвешенное
Данный показатель используется при расчете среднего арифметического для разных данных, каждое из которых имеет свой вес. Для определения взвешенного параметра необходимо каждое значение умножить на свой вес, суммировать эти произведения, после чего разделить на сумму весов.
В данном случае у нас есть средний вес каждого вида фруктов и его необходимо учесть для определения средней цены одного килограмма товара. На практике это выглядит так:
Среднее взвешенное = (20 × 24 + 10 × 54) / (24 + 54) = 13,07.
Естественно, 13,07 не сильно отличается от 15, однако чем больше слагаемых и больший разброс весов, тем сильнее отличается среднее взвешенное от простого среднего арифметического. Также очевидно, что если все веса равны единице, то среднее взвешенное становится равным среднему арифметическому.
Что выбрать?
Если требуется найти среднее значение одного элемента из однородного набора, то достаточно отыскать среднее арифметическое. Именно это мы делали при поиске среднего уровня продажи яблок или апельсинов за день. Если требуется найти среднее между разными элементами, принадлежащими к разным группам или отыскать среднее средних, то для расчета используется среднее арифметическое взвешенное.
Наша программа представляет собой калькулятор для расчета среднего арифметического и его взвешенного варианта. В меню калькулятора вы можете выбрать тип искомого параметра. Для расчета среднего арифметического вам понадобится ввести только значения параметров. В случае необходимости вы можете добавить дополнительные ячейки.
Для расчета взвешенного среднего выберите соответствующий пункт в меню калькулятора, укажите значения и их вес. Рассмотрим на примерах, как рассчитывать взвешенное значение.
Примеры из реальной жизни
Подсчет средней зарплаты
Пусть на вашем предприятии числятся сотрудники, каждый из которых получает зарплату в соответчики с должностью. Для рекламного проспекта о поиске персонала вы хотите уточнить, на какую среднюю зарплату может рассчитывать соискатель. Вы знаете, что:
Для вычисления средней зарплаты на предприятии вам потребуется ввести в ячейки значений размер зарплаты, а в ячейки весов — количество сотрудников, которые ее получают. Калькулятор мгновенно выдаст вам результат, что средняя зарплата равна 19 540 рублей. Без учета веса значений среднее арифметическое было бы равно 22 666 рублей, что уже значительно отличается от взвешенного значения.
Средняя скорость автомобиля
Допустим, водитель ехал по городскому проспекту со скоростью 60 км/ч в течение одного часа. Затем он выехал на автомагистраль, увеличил скорость до 120 км/ч и ехал так три часа, после чего свернул на проселочную дорогу и со скоростью 40 км/ч ехал еще два часа. С какой средней скоростью ехал водитель? В этой задаче в качестве веса выступает время езды, а значений — скорость. Выглядит это так:
Введем эти данные в форму калькулятора и получим ответ: средняя скорость автомобиля составляет 83,3 км/ч. Без учета времени средняя скорость была бы равна 73,3 км/ч, что неверно.
Заключение
Расчет среднего арифметического взвешенного широко используется в прикладных науках. Этот параметр популярен не только в статистике, но и в физике, экономике или финансах. Используйте наши калькуляторы в качестве помощника для решения практических и теоретических задач.
СРЕДНЕВЗВЕШЕННОЕ
Смотреть что такое «СРЕДНЕВЗВЕШЕННОЕ» в других словарях:
Средневзвешенное количество циркулирующих обыкновенных акций за период — количество обыкновенных акций, выпущенных и обращающихся на начало периода, скорректированное на количество погашенных, выкупленных эмитентом или выпущенных за период акций, умноженное на временной весовой множитель. По английски: Weighted… … Финансовый словарь
СРЕДНЕВЗВЕШЕННОЕ (СРЕДНЕЕ ЗНАЧЕНИЕ) — (weighted average, weighted mean) Среднее арифметическое значение, в котором учтены веса каждого из чисел, для которых рассчитывается это среднее значение. Например, если какое либо лицо покупает товар тремя партиями, одна из которых – 100 тонн… … Финансовый словарь
СРЕДНЕВЗВЕШЕННОЕ (CРЕДНЯЯ) — (weighted average) Средняя, в которой веса различных членов ряда пропорциональны их значимости. Средняя взвешенная N членов ряда х1, х2. xN находится путем суммирования его членов, умноженных на их веса w1, w2. wN, деленного на сумму… … Экономический словарь
Средневзвешенное количество циркулирующих обыкновенных акций за период — (average share volume) количество обыкновенных акций, выпущенных и обращающихся на начало периода, скорректированное на количество погашенных,выкупленных эмитентом или выпущенных за период акций, умноженное на временной весовой множитель … Экономико-математический словарь
средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted average; weighted… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
средневзвешенное значение — svertinis aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic weighted mean; weighted arithmetic average; weighted mean vok. Gewichteter arithmetischer Mittelwert, m; gewogener Mittelwert, m; gewogenes Mittelwert, m rus.… … Fizikos terminų žodynas
средневзвешенное значение — svertinis vidurkis statusas T sritis fizika atitikmenys: angl. weighted arithmetic average; weighted average; weighted mean vok. gewogener Mittelwert, m; gewogenes Mittel, n rus. взвешенное среднее, n; средневзвешенное значение, n pranc. moyenne… … Fizikos terminų žodynas
средневзвешенное по времени содержание — 3.2.1 средневзвешенное по времени содержание (time weighted average concentration): Содержание химического соединения в воздухе, усредненное за регламентированный период. Источник … Словарь-справочник терминов нормативно-технической документации
Средневзвешенное количество циркулирующих обыкновенных акций за период — Количество обыкновенных акций, выпущенных и обращающихся на начало периода, скорректированное на количество погашенных, выкупленных эмитентом или выпущенных за период акций, умноженное на временной весовой множитель … Финансы и биржа: словарь терминов
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
8.3. Средние величины в статистике
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
Таблица 8.2 – Результаты опроса работников офиса
Концепция взвешенного среднего или средневзвешенного значения (англ. ‘weighted mean’) неоднократно возникает в портфельном анализе. В среднем арифметическом значении все наблюдения одинаково взвешены с коэффициентом \(1/n\) (или \(1/N\)).
При работе с портфелями ценных бумаг нам нужна более общая концепция взвешенного среднего, позволяющая использовать разные веса для разных наблюдений.
Как рассчитать доходность этого инвестиционного портфеля?
Доходность портфеля явно предполагает усреднение доходов от инвестиций в акции и облигации. Однако значение, которое мы вычисляем, должно отражать тот факт, что акции имеют 70-процентный вес в портфеле, а облигации имеют 30-процентный вес.
Чтобы отразить это взвешивание, нужно умножить доходность инвестиций в акции на 0,70 и доходность инвестиций в облигации на 0,30, а затем суммировать два результата. Эта сумма является примером взвешенного среднего.
Было бы неправильно принимать среднее арифметическое значение доходности инвестиций в акции и облигации, равнозначно взвешивая доходность этих двух классов активов.
Рассмотрим другой портфель, инвестированный в канадские акции и облигации.
Компонент акций портфеля включает в себя канадский индексный Фонд акций RBC, который отслеживает эффективность индекса доходности S&P / TSX.
Облигационный компонент портфеля включает Фонд облигаций RBC, который инвестирует в высококачественные ценные бумаги с фиксированной доходностью, выпущенные правительствами и корпорациями Канады. Менеджер портфеля размещает 60% портфеля в фонд акций и 40% в фонд облигаций.
В Таблице 13 представлена общая доходность этих инвестиций с 2008 по 2012 год.