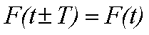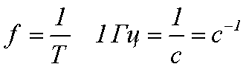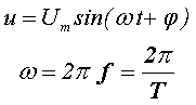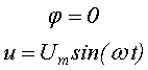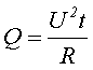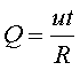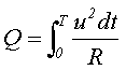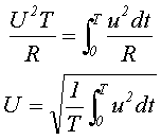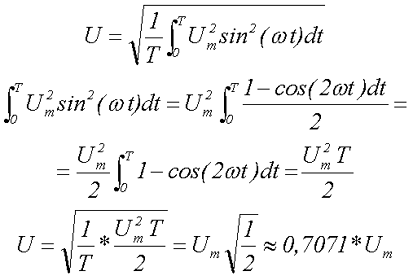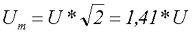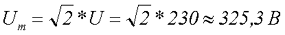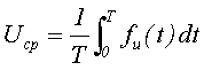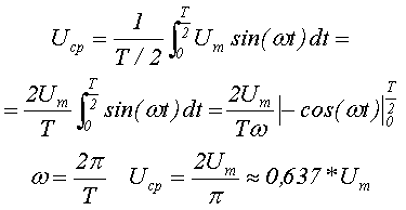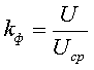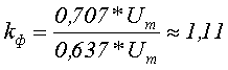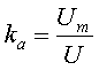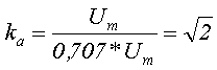Что такое среднее значение переменного тока
Среднее значение переменного тока
Среднее значение переменной синусоидальной величины за период равно нулю. Поэтому, когда говорят о среднем значении синусоидальной величины, имеют в виду среднее значение за полпериода. На рисунке 1 изображена кривая изменения переменного тока за полпериода.
Рисунок 1. Среднее значение синусоидального тока
Построим прямоугольник с основанием T/2 и площадью, равной площади, заключенной между кривой и горизонтальной осью. Высота прямоугольника будет представлять среднее значение тока за полпериода.
Высшая математика дает следующую зависимость между средним и амплитудным значениями переменного синусоидального тока:
Такая же зависимость существует между средними и амплитудными значениями напряжения и электродвижущей силы (ЭДС). Среднее значение напряжения и ЭДС равно:
Отношение действующего значения переменной величины к ее среднему значению называется коэффициентом формы кривой и обозначается буквой kф.
Для синусоидальных величин коэффициент формы кривой равен:
Отношение амплитудного значения переменной величины к ее действующему значению называется коэффициентом амплитуды и обозначается kа.
Для синусоидальных величин коэффициент амплитуды
2.9. Действующее и среднее значения переменного тока и напряжения
Действующим значением переменного тока или напряжения называют корень квадратный от интеграла квадрата мгновенных значений тока или напряжения на периоде повторения.
Пользуясь определением, найдем действующее значение синусоидального тока:
После аналогичных вычислений для напряжения получим:
Таким образом, действующие значения переменного тока и напряжения меньше их амплитудных значений в 
Действующее значение переменного тока в одной и той же нагрузке r способствует выделению такой тепловой энергии, которая выделилась бы, если по нагрузке пропустить постоянный ток той же величины.
В комплексном виде действующие значения напряжения и тока имеют вид:

Средним по модулю значением напряжения или тока называют интеграл от модуля мгновенного значения тока или напряжения на периоде повторения.
Найдем среднее значение переменного напряжения:
Средние значения напряжения и тока меньше их амплитудных значений в
Параметры переменного напряжения
Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.
Среднее значение напряжения
Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.
Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.
То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.
Средневыпрямленное значение напряжения
Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.
средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.
На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:
Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:
Среднеквадратичное значение напряжения
Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.
Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды Ka:
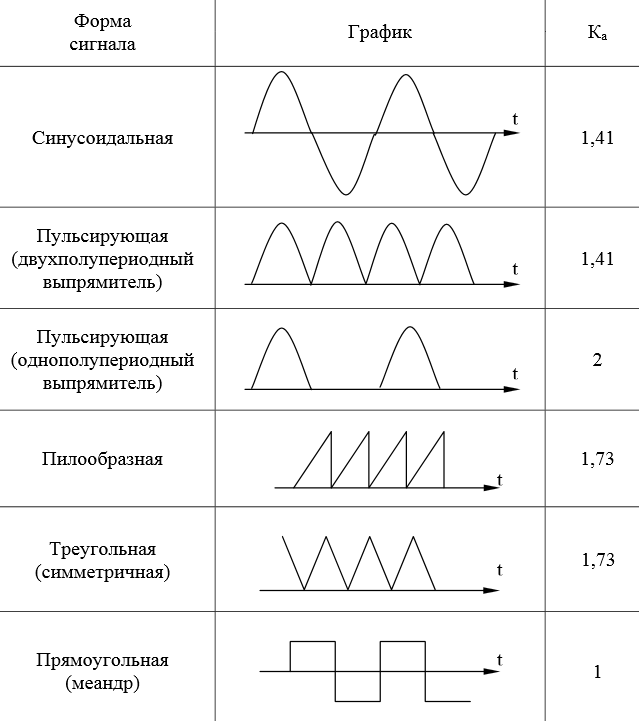
Вот некоторые значения коэффициента амплитуды Ka для некоторых сигналов переменного напряжения:
Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.
Как измерить среднеквадратичное значение напряжения
Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.
Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

Проведем небольшой опыт. Давайте соберем вот такую схемку:
Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц
генератор частоты
А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?
Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:
Итак, смотрим нашу табличку и находим интересующий нас сигнал:
Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды Ka= 1,73.
Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала
Проверяем нашим прибором, так ли оно на самом деле?
Супер! И в правду Тrue RMS.
Замеряем это же самое напряжение с помощью моего китайского мультиметра
Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.
Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».
Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.
Вот вам небольшая картинка, чтобы не путаться
Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.
Действующее и среднее значения переменного тока
Основной задачей расчета электрической цепи является определение тока. В цепях постоянного тока, если нет регулирующих устройств, ток остается неизменным и его легко рассчитать или измерить. В цепях переменного тока ток непрерывно меняется по величине и по направлению. Если, допустим, что каким-либо путем нам удалось определить одно мгновенное значение тока, то это не даст оценки действия всех остальных значений.
Поэтому переменный ток оценивается по его действию, которое эквивалентно действию некоторого постоянного тока. В качестве критерия такой эквивалентности принято считать тепловое действие тока.
Действующее значение переменного тока численно равно такому постоянному току, который в элементе цепи за время, равное периоду Т, выделяет такое же количество тепла, какое в том же элементе за то же время при тех же условиях выделяет переменный ток.
Определим количество тепла, которое выделяется за период Т постоянным током.
По закону Джоуля – Ленца:



Для переменного тока

По определению количество тепла, выделяемое постоянным и переменным токами, должно быть одинаково.


Тогда действующее значение тока определится выражением

Полученное выражение справедливо для любого переменного тока независимо от его формы.
Определим действующее значение синусоидального тока. Представим мгновенное значение тока в виде 

Используя правила тригонометрических преобразований, выразим


Отсюда 

Действующее значение синусоидального тока в 
То же самое можно сказать о напряжении и ЭДС:


Действующие значения токов, напряжений и ЭДС обозначаются прописной буквой без индекса. Все расчеты в цепях переменного тока выполняются для действующих значений токов, напряжений и ЭДС.
Действующее значение переменного тока можно измерить приборами любой системы, кроме магнитоэлектрической.
Отношение амплитуды к действующему значению тока называется коэффициентом амплитуды.
Для синусоидальных токов коэффициент амплитуды всегда равен 

В ряде случаев при анализе электрических цепей переменного тока необходимо определить среднее значение переменного тока.
Средним значением переменного тока называется среднее арифметическое из всех мгновенных значений за половину периода.
Для синусоидальных величин среднее значение всегда оценивается за половину периода, так как мгновенные значения полпериода положительны, а полпериода – отрицательны, в результате среднее значение за период равно нулю.
Найдем среднее значение переменного тока:

Учтем, что 

Отношение действующего значения к среднему называется коэффициентом формы кривой.

Учтем, что 

Подставив эти значения в формулу коэффициента формы, получим для синусоидального тока

Таким образом, действующие значения тока, напряжения и э.д.с. связаны со средними значениями соотношениями:



ElectronicsBlog
Обучающие статьи по электронике
Переменное напряжение и его параметры
Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.
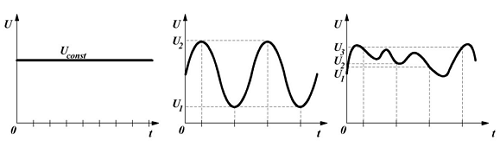
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже
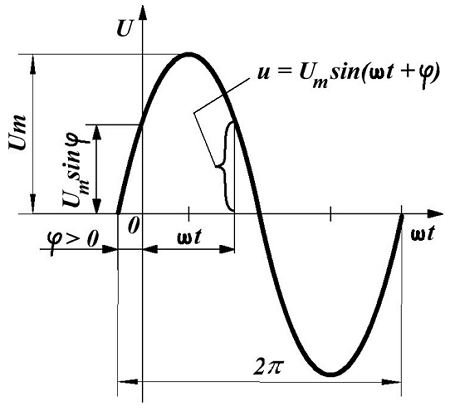
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
Для переменного напряжения мгновенное значение выделяемой энергии составит
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
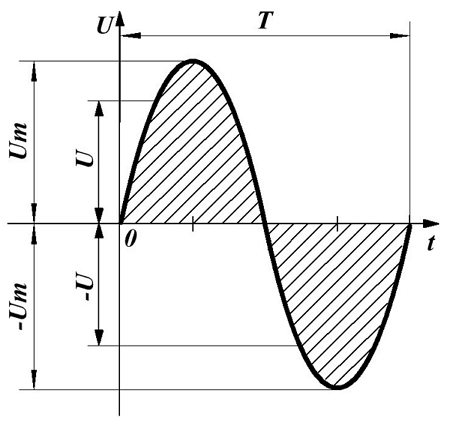
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
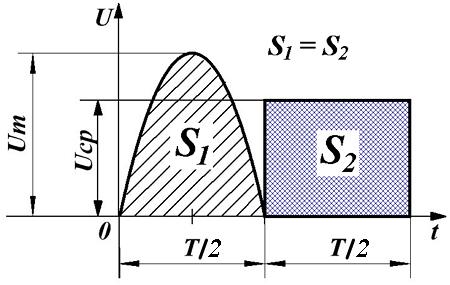
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Какие коэффициенты, характеризуют переменное напряжение?
Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:
1. Коэффициент формы переменного напряжения kф – показывает как относится действующее значение переменного напряжения U к его среднему значению Ucp.
Так для синусоидального напряжения коэффициент формы составит
2. Коэффициент амплитуды переменного напряжения kа – показывает как относится амплитудное значение переменного напряжения Um к его действующему значению U
Так для синусоидального напряжения коэффициент амплитуды составит
На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.
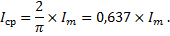

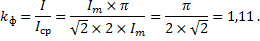
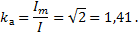







.png)