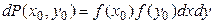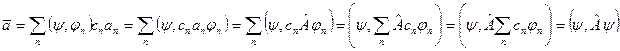Что такое среднее значение в физике

Вычисление средних значений физических величин

Для характеристики случайной величины часто пользуются понятием среднего значения, которое определяется как:

(14)

Мерой отличия случайной величины x от среднего значения является дисперсия (среднеквадратичное отклонение), которая определяется как:

(15)

Раскрывая скобки и пользуясь определением средних величин можно получить простое выражение для расчета дисперсии:

(16)

.

Для расчета дисперсии биноминального распределения воспользуемся формулой (15) и результатом вычисления . Расчет можно провести аналогично :

Подстановка этой формулы в (15) приводит к значению дисперсии в биноминальном распределении:

Вычисление средних значений физических величин, зависящих от случайной величины x, проводится аналогично (14). Если известны вероятности различных состояний системы p_i, при этом требуется вычислить значения какой-либо физической величины u имеющей разные значения в каждом из состояний u_i=u(x_i). Вычисление среднего значения производится в соответствии с формулой:

(17)

В случае непрерывного распределения вероятности выражение для среднего значения величины u(x) определяется через функцию плотности вероятности f(x):

(15)

Распределение Гаусса

Распределение Гаусса достаточно часто встречается при описании реальных физических систем. Одной из основных задач, приводящих к получению распределения Гаусса, является задача о случайном блуждании частицы на плоскости. Если частица начинает блуждания из начала координат, то вероятность ее обнаружения через некоторое время в области площадью dxdy в окрестности точки (x₀, y₀), определяется в виде:

(16)

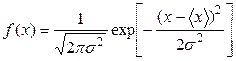
Здесь — среднее значение случайной величины x, — среднеквадратичное отклонение случайной величины x. График функции f(x) приведен на рис.2

Распределение Максвелла

Распределение Максвелла определяет функцию распределения частиц идеального газа по скоростям. По своему виду распределение Максвелла совпадает с распределением Гаусса, когда в качестве случайных величин выбираются проекции скорости молекул. Функция плотности вероятности для проекции скорости :

(17)

Поскольку компоненты скорости являются независимыми, то выражение (17) может быть перенесено и на компоненты скорости и . Общий вид графика функции (17) соответствует зависимости представленной на рис. 2.

В соответствии с (17) может быть получено распределение по модулю скорости:

(18)

График функции F(v) зависит от температуры

Распределение Максвелла F(v) может быть охарактеризовано несколькими характерными значениями скорости:

,

где — среднее значение модуля скорости, — наиболее вероятное значение скорости, — среднеквадратичное значение модуля скорости.

Вычисление среднего значения кинетической энергии молекул идеального газа, описываемых распределением Максвелла, может быть получено в виде:

(19)

Методика моделирования

Рассмотрим N частиц, идеального газа, имеющих одинаковую массу m, находящихся в закрытом сосуде. Каждая из частиц характеризуется вектором скорости или проекциями скоростей v_xi, v_yi, v_zi.

Предположим, что в начальный момент времени частицы идеального газа являются неподвижными. Поскольку частицы являются неподвижными, то кинетическая энергия равна нулю, а, следовательно, и температура, соответствующая такому состоянию, равна нулю (см. формулу (19)).

Если частицы газа взаимодействуют с поверхностью сосуда (посредством абсолютно упругого удара, т.е. условие идеальности газа не нарушается), находящегося при некоторой температуре T_сосуда, то температура газа постепенно увеличиваться до тех пор пока не будет достигнуто состояние термодинамического равновесия и температура газа не станет равной T_газа=T_сосуда. При каждом акте соударения со стенками сосуда происходит случайное изменение проекций импульса частиц газа. Предположим, что при каждом соударении (либо между собой, либо со стенками сосуда) изменяется только одна из проекций импульса на некоторую малую случайную величину Dp.

Таким образом, в системе реализуется случайное блуждание частиц из начального состояния (v_xi=0, v_yi=0, v_zi=0) с постоянным шагом Dp/m. При чем на каждом шаге изменяется только одна из проекций скорости. Так как температура газа имеет связь со средней кинетической энергией, то случайное блуждание в пространстве импульсов прекращается при достижении термодинамического равновесия со стенками сосуда (т.е. при равенстве температуры газа и температуры сосуда):

.

В результате расчета распределение частиц по скоростям будет соответствовать распределению Максвелла, записанному в формулах (17) и (18).

3. Практические задания

Выполнение работы с помощью программы LabStat.exe. Внешний вид программы представлен на рис.4. Для выполнения упражнений 1-3 необходимо выбрать соответствующую кнопку в диалоговом окне программы.

Рисунок 4Внешний вид программы LabStat.exe

Первые два упражнения являются ознакомительными, поскольку позволяют с помощью вычислительного эксперимента познакомиться с некоторыми закономерностями теории вероятностей, применяемыми в молекулярной физике.

В третьем упражнении предлагается проведение моделирования распределения частиц по проекции скорости и модулю скорости (распределение Максвелла).

Источник

Среднее арифметическое: физический смысл и визуализация

Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:

Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.

Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.

Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.

Среднее арифметическое двух чисел

Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:

Их среднее арифметическое:

Физический смысл среднего арифметического

Изобразим два исходных числа и их среднее арифметическое на числовой оси:

Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.

В механике момент силы – это произведение силы F на расстояние l:

На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l₁ и l₂, получим:

Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:

Обозначив m координату точки опоры весов, получим:

Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:

Координата опоры весов m:

Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.

Визуальное восприятие равновесия

Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.

Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:

На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.

Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:

Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.

Математическое ожидание случайной величины

Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:

Теперь точка опоры весов в равновесии это μ:

Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:

Это и есть формула математического ожидания.

Гистограмма

Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.

На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.

Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:

Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:

Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:

Дайте мне точку опоры, и я переверну Землю. Архимед

Источник

СРЕДНЕЕ ЗНАЧЕНИЕ

— то же, что математическое ожидание.

Смотреть что такое СРЕДНЕЕ ЗНАЧЕНИЕ в других словарях:

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ (average) Статистический обобщенный показатель какой-либо величины. Среднее ряда чисел может быть взвешенным или невзвешенным. Невз. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

(mean) См.: арифметическое среднее (arithmetic mean); геометрическое среднее (geometric mean); медиана (median).Бизнес. Толковый словарь. — М.: «ИНФРА-. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

числовая характеристика группы чисел или функций. Для группы чисел наиб. употребительными С. з. являются: арифметическое среднее, гармоническое среднее. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

1. snitt boxern blir i snitt tio år gammal—боксёры (порода собак) живут в среднем 10 лет

СРЕДНЕЕ ЗНАЧЕНИЕ

показатель, который принимает случайная переменная, равный средневзвешенной всех возможных значений переменной, в которой весами являются вероятности соответствующих событий. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

сDurchschnittswert (m) Durchschnitt (m); Mittelwert (m); Mittel (n)

СРЕДНЕЕ ЗНАЧЕНИЕ

1) average value2) <math.> mean3) mean value4) population mean

СРЕДНЕЕ ЗНАЧЕНИЕ

MEAN) Среднее арифметическое или среднее ряда значений получается делением суммы этих значений на их число (п) в данном ряду.

СРЕДНЕЕ ЗНАЧЕНИЕ

(оценка текущей цены путем расчета среднего репрезентативной выборки совершенных сделок) average measures, average value

СРЕДНЕЕ ЗНАЧЕНИЕ

midvalue, medium, average value, mean value* * *mean

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

(медиана) midscore; average value

СРЕДНЕЕ ЗНАЧЕНИЕ

Durchschnitt, Durchschnittswert, Mittelwert

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

average value, mean value, mean

СРЕДНЕЕ ЗНАЧЕНИЕ

• průměrná hodnota• střední hodnota

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

measurement average, average, mean value

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

average value, mean value

СРЕДНЕЕ ЗНАЧЕНИЕ

moyenne, valeur moyenne

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

media, valore medio

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ БЕЗРАЗМЕРНОГО АКУСТИЧЕСКОГО ИМПЕДАНСА

average acoustic impedance ratio

СРЕДНЕЕ ЗНАЧЕНИЕ ВЕЛИЧИНЫ

3.14 среднее значение величины: Средневзвешенное значение величины за определенный период времени (час, сутки). Источник: ГОСТ Р 8.733-2011: Государ. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ (ВЫБОРОЧНОЕ)

СРЕДНЕЕ ЗНАЧЕНИЕ ВЫБОРОЧНОЙ СОВОКУПНОСТИ

Среднее арифметическое, то есть сумма показателей, деленная на их количество.

СРЕДНЕЕ ЗНАЧЕНИЕ ГАРМОНИЧЕСКОЕ

гармоникалық орта мән

СРЕДНЕЕ ЗНАЧЕНИЕ ГЕОДЕЗИЧЕСКОЕ

геодезиялық орта мән

СРЕДНЕЕ ЗНАЧЕНИЕ ИЗБЫТОЧНОГО ДАВЛЕНИЯ В ПОДМАСОЧНОМ ПРОСТРАНСТВЕ ЛИЦЕВОЙ ЧАСТИ

3.8 среднее значение избыточного давления в подмасочном пространстве лицевой части: Среднеарифметическое значение величин избыточного давления воздух. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ИЗМЕРЕНИЙ

Среднее значение измерений (mean value of measurements) — частное от деления алгебраической суммы значений измерений на число измерений.Примечание. Сре. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ИНДУКТИВНОСТИ КАТУШКИ

40. Среднее значение индуктивности катушки Е. Mean value of inductance F. Valeur moyenne ďinductance Источник: ГОСТ 20718-75: Катушки индуктивности. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ИНТЕРВАЛА

СРЕДНЕЕ ЗНАЧЕНИЕ МАССЫ ДОЗЫ

СРЕДНЕЕ ЗНАЧЕНИЕ МОДУЛЯ

mean value of modulus

СРЕДНЕЕ ЗНАЧЕНИЕ МОДУЛЯ КОЛЕБЛЮЩЕЙСЯ ВЕЛИЧИНЫ

23. Среднее значение модуля колеблющейся величины Среднее значение модуля Ндп. Средневыпрямленное значение (Поправка). Среднее арифметическое или ср. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ МОЩНОСТИ ФЛУКТУАЦИИ

mean fluctuation power

СРЕДНЕЕ ЗНАЧЕНИЕ НАБЛЮДАЕМОЙ

expectation value of an observable

СРЕДНЕЕ ЗНАЧЕНИЕ НАБЛЮДЕНИЙ

СРЕДНЕЕ ЗНАЧЕНИЕ НАПРЯЖЕНИЙ

СРЕДНЕЕ ЗНАЧЕНИЕ ОПЕРАТИВНОЙ ПРОДОЛЖИТЕЛЬНОСТИ КОРРЕКТИРУЮЩЕГО ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ

155 среднее значение оперативной продолжительности корректирующего технического обслуживания: Математическое ожидание оперативной продолжительности к. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ПАРАМЕТРА ПОТОКА ОТКАЗОВ ЕДИНИЦЫ

61 среднее значение параметра потока отказов единицы [составной части единицы] (железнодорожного) тягового подвижного состава: Отношение числа отказо. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ПАРАМЕТРА ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ

Источник

Вычисление средних значений физических величин

Расчет средних значений физических величин имеет важное значение в микромире. Когда в рассматриваемом состоянии квантовомеханической системы физическая величина не имеет определенного значения, т.е. при измерении этой физической величины получается неоднозначный результат, то среднее значение этой величины в какой-то мере характеризует состояние.

(5.9)

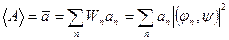
Учитывая свойства скалярных произведений векторов гильбертова пространства (4.7) и (4.10), получим

Таким образом, для расчета среднего значения физической величины А, изображающейся соответствующим оператором Â, необходимо знать вектор состояния y:

(5.10)

(5.11)

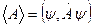
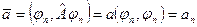
Если ( Ψ,Ψ ) ≠ 1, тогда для среднего значения физической величины справедливо выражение:

(5.12)

Источник

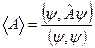
Формула скорости — обозначение, единицы измерения и примеры нахождения

Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Источник