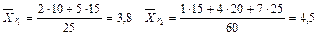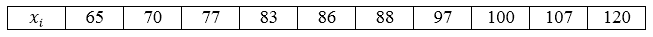Что такое среднее значение выборки
Характеристики выборки и генеральной совокупности
Основные понятия математической статистики
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использованию статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками.
Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой. Число объектов N из генеральной совокупности и из выборки n называются соответственно объемом генеральной совокупности N и объемом выборки n.
Статистическое описание и вероятностные модели применяются к физическим, экономическим, социологическим, биологическим процессам, обладающим тем свойством, что хотя результат отдельного измерения физической величины X не может быть предсказан с достаточной точностью, но значение некоторой функции 

Наиболее известные статистики – относительная частота, выборочные средние, дисперсия. Когда возрастает объем выборки n, многие выборочные статистики сходятся по вероятности к соответствующим параметрам теоретического распределения величины X. Поэтому каждую выборку рассматривают как выборку из теоретически бесконечной генеральной совокупности, распределение признака в которой совпадает с теоретическим распределением вероятности случайной величины. Во многих случаях теоретическая генеральная совокупность есть идеализация действительной совокупности, из которой получена выборка.
Различные значения наблюдаемого признака, встречающегося в совокупности, называются вариантами. Частоты вариантов выражают доли (удельные веса) элементов совокупности с одинаковыми значениями признака. Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующим им частотами.
Средние значения выборки
Среднее арифметическое значение генеральной совокупности 



или же 
для негруппированных выборок и

для группированных выборок, где




Пример 1. В таблице даны значения средней температуры воздуха в населённом пункте N в 2014 году:
| Месяц |  |
| 1 | -2,3 |
| 2 | -4,0 |
| 3 | 2,0 |
| 4 | 9,0 |
| 5 | 10,0 |
| 6 | 19,4 |
| 7 | 19,9 |
| 8 | 17,1 |
| 9 | 14,9 |
| 10 | 7,3 |
| 11 | 2,2 |
| 12 | -0,3 |
Найти среднюю температуру воздуха.
Решение. Найдём среднюю температуру воздуха как среднее значение для негруппированной выборки:
Пример 2. В таблице – данные о группировке сельских хозяйств по урожайности зерновых:
Урожайность зерновых в центнерах с га
Число сельских хозяйств – абсолютное
Удельный вес сельских хозяйств – в процентах
Выборочная средняя и выборочная дисперсия



Пусть для изучения генеральной совокупности относительно количественного признака Х произведена выборка объёма n.
Выборочной средней 
Если все значения х1, х2, …, хn выборки различны, то
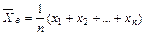 | (7.1) |
 | (7.2) |
Иногда бывает целесообразным выборочные значения случайной величины разбить на отдельные группы. Для каждой группы можно найти её среднюю.
Групповой средней 
По групповым средним можно найти среднее для всей выборки.
Общей средней 
Пример 7.1.Найти общую среднюю на основе выборки.
Решение: Находим групповые средние:
Если варианты хi – большие числа, то для облегчения вычисления выборочной средней используют следующий приём. Пусть С – константа.

 | (7.3) |
Пример 7.2.Имеется выборка:
| х1=71,88 | х2=71,93 | х3=72,05 | х4=72,07 | х5=71,90 |
| х6=72,02 | х7=71,93 | х8=71,77 | х9=71,77 | х10=71,96 |
Найти выборочную среднюю.
Решение: Берем С=72 и вычисляем разности
| α1=-0,12 | α2=-0,07 | α3=0,05 | α4=0,07 | α5=-0,10 |
| α6=0,02 | α7=-0,07 | α8=-0,23 | α9=0,11 | α10=-0,04 |
Их сумма: α1+α2+…+α10=-0,38; их среднее арифметическое: 

Для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки относительно выборочного среднего вводят понятие выборочной дисперсии.
Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонений наблюдаемых значений признака Х от выборочной средней 
Если все значения х1, х2, …, хn признака выборки объёма n различны, то
 | (7.4) |
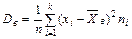 | (7.5) |
Пример 7.3.Выборочная совокупность задана таблицей распределения:
| xi | 1 | 2 | 3 | 4 |
| ni | 20 | 15 | 10 | 5 |
Найти выборочную дисперсию.
Решение: Согласно формулам (7.2) и (7.5) имеем:

Выборочным средним квадратическим отклонением называется квадратный корень из выборочной дисперсии:
Можно доказать, что
 | (7.6) |
 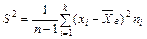 | (7.7) |
Исправленная дисперсия (7.7) является несмещенной оценкой генеральной дисперсии
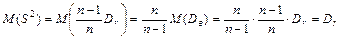 |
Если варианты хi – большие числа, то для облегчения вычисления выборочной дисперсии Dв формулу (7.4) преобразуют к следующему виду:
 | (7.8) |
где С – ложный нуль.
Пример 7.4.Через каждый час измерялось напряжение тока в электросети. Результаты измерений в вольтах представлены в таблице 7.1:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| xi | 222 | 219 | 224 | 220 | 218 | 217 | 221 | 220 | 215 | 218 | 223 | 225 |
| i | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| xi | 220 | 226 | 221 | 216 | 211 | 219 | 220 | 221 | 222 | 218 | 221 | 219 |
Найти оценки для математического ожидания и дисперсии результатов измерений.
Решение: Оценки для математического ожидания и дисперсии найдем по формулам (7.3) и (7.8), положив С=220. Все необходимые вычисления приведены в таблице 7.2:
Средняя выборки: генеральная, выборочная
Вы будете перенаправлены на Автор24
Генеральная средняя
Выборочная средняя
Готовые работы на аналогичную тему
Примеры задач на нахождение средней выборки
В магазин завезли 10 видов шоколадных конфет. По ним проведена следующая выборка по цене за килограмм: 70, 65, 97, 83, 120, 107, 77, 88, 100, 86. Построить ряд распределения данной генеральной совокупности и найти её генеральное среднее.
Видим, что все значения вариант различны, поэтому частоты равны единице. Ряд распределения можно записать следующим образом, перечислив значения вариант в порядке возрастания:
Так как наша совокупность является генеральной и все варианты различны, то мы будем пользоваться следующей формулой:
Выборочная совокупность задана следующей таблицей распределения:
Найти среднее выборочное данной совокупности.
Для нахождения значения выборочной средней будем пользоваться следующей формулой:
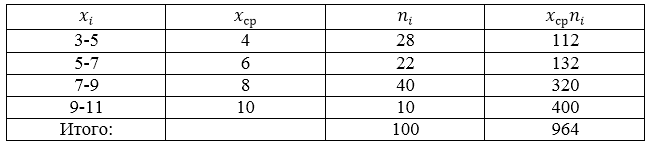
Обычно, для наглядности и удобности вычислений составляется расчетная таблица, в которую входят необходимые промежуточные вычисления. В нашем случае составим таблицу со следующей «шапкой»:
Внизу таблицы также добавляется строка «итог», в которой подсчитывается сумма по всем значениям столбцов. Проведя необходимые вычисления, получим следующую расчетную таблицу:
Используя формулу, получим:
Проводится социальный опрос среди 100 пенсионеров об уровне их пенсии. Получена следующая таблица распределения результатов опроса (размер пенсии указан в тысячах рублей):
Найти среднее выборочное данной совокупности.
Данная совокупность является выборочной, поэтому будем пользоваться следующей формулой:
Составим, для начала, расчетную таблицу.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 25 02 2021
Алгебра
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:
Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.
В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.
Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.
Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.
Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:
При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.
Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
в то время как размах выборки второго спортсмена равен
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:
Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:
Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.