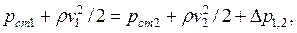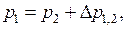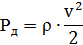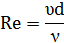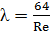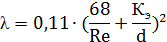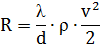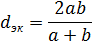Что такое статическое давление в потоке

Параметры воздушного потока

Под действием вентилятора в трубопроводе создается воздушный поток. Важными параметрами воздушного потока являются его скорость, давление, плотность, массовый и объемный расходы воздуха.

Расходы воздуха объемный Q, м 3 /с, и массовый М, кг/с, связаны между собой следующим образом:

; , (3)

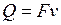
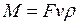
где F – площадь поперечного сечения трубы, м 2 ;

v – скорость воздушного потока в заданном сечении, м/с;

Давление в воздушном потоке различают статическое, динамическое и полное.

Статическим давлением Р_ст принято называть давление частиц движущегося воздуха друг на друга и на стенки трубопровода. Статическое давление отражает потенциальную энергию воздушного потока в том сечении трубы, в котором оно измерено.

Динамическое давление воздушного потока Р_дин, Па, характеризует его кинетическую энергию в сечении трубы, где оно измерено:

.

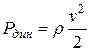
Полное давление воздушного потока определяет всю его энергию и равно сумме статического и динамического давлений, измеренных в одном и том же сечении трубы, Па:

Отсчет давлений можно вести либо от абсолютного вакуума, либо относительно атмосферного давления. Если давление отсчитывается от нуля (абсолютного вакуума), то оно называется абсолютным Р. Если давление измерять относительно давления атмосферы, то это будет относительное давление Н.

Атмосферное давление равно разности полных давлений абсолютного и относительного

Давление воздуха измеряют Па (Н/м 2 ), мм водяного столба или мм ртутного столба:

1 мм вод. ст. = 9,81 Па; 1 мм рт. ст. = 133,322 Па. Нормальное состояние атмосферного воздуха соответствует следующим условиям: давление 101325 Па (760 мм рт. ст.) и температура 273К.

Плотность воздуха есть масса единицы объема воздуха. По уравнению Клайперона плотность чистого воздуха при температуре 20ºС

где R – газовая постоянная, равная для воздуха 286,7 Дж/(кг × К); T – температура по шкале Кельвина.

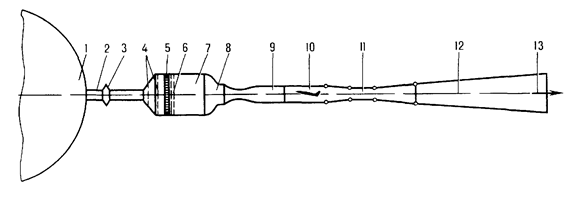
Уравнение Бернулли. По условию неразрывности воздушного потока расход воздуха постоянен для любого сечения трубы. Для сечений 1, 2 и 3 (рис. 6) это условие можно записать так:

;

. (4)

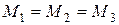
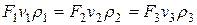
При изменении давления воздуха в пределах до 5000 Па плотность его остается практически постоянной.

В связи с этим:

;

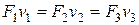
Изменение давления воздушного потока по длине трубы подчиняется закону Бернулли. Для сечений 1, 2 можно написать

(5)

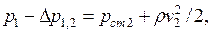
где Dр_1,2 – потери давления, вызванные сопротивлением потока о стенки трубы на участке между сечениями 1 и 2, Па.

С уменьшением площади поперечного сечения 2 трубы скорость воздуха в этом сечении увеличится, так что объемный расход останется неизменным. Но с увеличением v₂ возрастет динамическое давление потока. Для того, чтобы равенство (5) выполнялось, статическое давление должно упасть ровно на столько, на сколько увеличится динамическое давление.

При увеличении площади сечения динамическое давление в сечении упадет, а статическое ровно на столько же увеличится. Полное же давление в сечении останется величиной неизменной.

Источник

Полное, статическое и динамическое давление. Измерение давления в воздуховодах систем вентиляции

Полное, статическое и динамическое давление

При движении воздуха по ВВ в любом поперечном сечении различают 3 вида давления:

Статическое давление определяет потенциальную энергию 1 м 3 воздуха в рассматриваемом сечении. Оно равно давлению на стенки воздуховода. .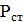

Динамическое давление – кинетическаяя энергия потока, отнесенная к 1 м 3 воздуха.

– плотность воздуха,

— скорость воздуха, м/с.

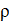
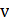
Полное давление равно сумме статического и динамического давления.

Принято пользоваться значением избыточного давления, принимая за условный ноль атмосферное давление на уровне системы. В нагнетательных воздуховодах полное и статическое избыточное давление всегда «+», т.е. давление > 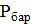. Во всасывающих воздуховодах полное и статическое избыточное давление «-».

Измерение давления в воздуховодах систем вентиляции

Давление в ВВ измеряется при помощи пневмометрической трубки и какого-либо измерительного прибора: микроманометра либо др.прибора.

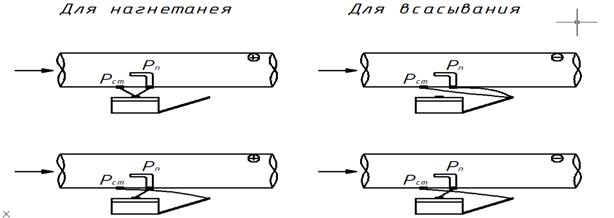
Для нагнетательного воздуховода:

статическое давление – трубку статического давления к бачку микроманометра;

полное давление – трубку полного давления к бачку микроманометра;

динамическое давление – трубку полного давления к бачку, а статического – к капилляру микроманометра.

Для всасывающего воздуховода:

статическое давление – трубку статического давления к капилляру манометра;

полное давление – трубку полного давления к капилляру микроманометра;

динамическое давление – трубку полного давления к бачку, а статического – к капилляру микроманометра.

Схемы измерения давления в воздуховодах.

Билет №10

Потери давления в системах вентиляции

При движении по ВВ воздух теряет свою энергию на преодоление различных сопротивлений, т.е. происходят потери давления.

Потери давления на трение

– коэффициент сопротивления трения. Зависит от режима движения жидкости по воздуховоду.

— кинематическая вязкость, зависит от температуры.

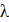
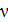
При ламинарном режиме:

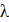
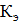
при турбулентном движении зависит от шероховатости поверхности трубы. Применяются различные формулы и широко известна формула Альтшуля:

– абсолютная эквивалентная шероховатость материала внутренней поверхности воздуховода, мм.

Для листовой стали 0,1мм; силикатобетонные плиты 1,5 мм; кирпич 4 мм, штукатурка по сетке 10 мм

Удельные потери давления

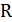
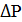
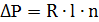
В инженерных расчетах пользуются специальными таблицами, в которых приводят значения для круглого воздуховода. Для воздуховодов из других материалов вводится поправочный коэффициент и равно:

.

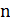
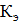
Значение поправочного коэффициента приводится к справочнике в зависимости от вида материала и от скорости перемещения воздуха по воздуховоду.

Для прямоугольных воздуховодов за расчетную величину d принимают эквивалентныйdэк, при которой потери давления в круглом воздуховоде при той же скорости будут равны потерям давления в прямоугольном воздуховоде:

— стороны прямоугольного воздуховода.

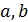
Следует иметь в виду: расход воздуха прямоугольного и круглого воздуховодов с 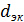при равенстве скоростей не совпадает.

Дата добавления: 2018-02-18 ; просмотров: 25495 ; Мы поможем в написании вашей работы!

Источник

СТАТИЧЕСКОЕ ДАВЛЕНИЕ И СКОРОСТНОЙ НАПОР УРАВНЕНИЕ БЕРНУЛЛИ

(1.11)

где m— масса воздуха, кгс с 2 м; V-скорость воздушного потока, м/с. Если вместо массы m подставить массовую плотность воздуха р, то получим формулу для определения скоростного напора q (в кгс/м 2 )

. (1.12)

(1.15)

Из уравнения видно, что внутренняя энергия воздушного потока прямо пропорциональна его температуре.

Ввиду мизерно малых значений разноса центров тяжести масс воздуха по высоте в струйке воздушного потока этой энергией в аэродинамике пренебрегают.

Рассматривая во взаимосвязи все виды энергии применительно к определенным условиям, можно сформулировать закон Бернулли, который устанавливает связь между статическим давлением в струйке воздушного потока и скоростным напором.

Рассмотрим трубу (Рис. 10) переменного диаметра (1, 2, 3), в которой движется воздушный поток. Для измерения давления в рассматриваемых сечениях используют манометры. Анализируя показания манометров, можно сделать заключение, что наименьшее динамическое давление показывает манометр сечения 3-3. Значит, при сужении трубы увеличивается скорость воздушного потока и давление падает.

Рис. 10 Объяснение закона Бернулли

Причиной падения давления является то, что воздушный поток не производит никакой работы (трение не учитываем) и поэтому полная энергия воздушного потока остается постоянной. Если считать температуру, плотность и объем воздушного потока в различных сечениях постоянными (T₁=T₂=T₃;р₁=р₂=р₃, V1=V2=V3), то внутреннюю энергию можно не рассматривать.

Значит, в данном случае возможен переход кинетической энергии воздушного потока в потенциальную и наоборот.

Когда скорость воздушного потока увеличивается, то увеличивается и скоростной напор и соответственно кинетическая энергия данного воздушного потока.

Подставим значения из формул (1.11), (1.12), (1.13), (1.14), (1.15) в формулу (1.10), учитывая, что внутренней энергией и энергией положения мы пренебрегаем, преобразуя уравнение (1.10), получим

(1.17)

Это уравнение для любого сечения струйки воздуха пишется следующим образом:

Такой вид уравнения является самым простым математическим уравнением Бернулли и показывает, что сумма статического и динамического давлений для любого сечения струйки установившегося воздушного потока есть величина постоянная. Сжимаемость в данном случае не учитывается. При учете сжимаемости вносятся соответствующие поправки.

Для наглядности закона Бернулли можно провести опыт. Взять два листка бумаги, держа параллельно друг другу на небольшом расстоянии, подуть в промежуток между ними.

Рис. 11 Измерение скорости воздушного потока

Листы сближаются. Причиной их сближения является то, что с внешней стороны листов давление атмосферное, а в промежутке между ними вследствие наличия скоростного напора воздуха давление уменьшилось и стало меньше атмосферного. Под действием разности давлений листки бумаги прогибаются вовнутрь.

АЭРОДИНАМИЧЕСКИЕ ТРУБЫ

Экспериментальная установка для исследования явлений и процессов, сопровождающих обтекание тел потоком газа называется аэродинамической трубой. Принцип действия аэродинамических труб основан на принципе относительности Галилея: вместо движения тела в неподвижной среде изучается обтекание неподвижного тела потоком газа В аэродинамических трубах экспериментально определяются действующие на ЛА аэродинамические силы и моменты исследуются распределения давления и температуры по его поверхности, наблюдается картина обтекания тела, изучается аэроупругость и т д.

Компрессорные трубы имеют высокий кпд, они удобны в работе, но требуют создания уникальных компрессоров с большими расходами газа и большой мощности. Баллонные аэродинамические трубы по сравнению с компрессорными менее экономичны, поскольку при дросселировании газа часть энергии теряется. Кроме того, продолжительность работы баллонных аэродинамических труб ограничена запасом газа в баллонах и составляет для различных аэродинамических труб от десятков секунд до несколько минут.

Широкое распространение баллонных аэродинамических труб обусловлено тем, что они проще по конструкции а мощности компрессоров, необходимые для наполнения баллонов, относительно малы. В аэродинамических трубах с замкнутым контуром используется значительная часть кинетической энергии, оставшейся в газовом потоке после его прохождения через рабочую область, что повышает КПД трубы. При этом, однако, приходится увеличивать общие размеры установки.

В дозвуковых аэродинамических трубах исследуются аэродинамические характеристики дозвуковых самолетов вертолетов а также характеристики сверхзвуковых самолетов на взлетно-посадочных режимах. Кроме того, они используются для изучения обтекания автомобилей и др. наземных транспортных средств, зданий, монументов, мостов и др. объектов На рис показана схема дозвуковой аэродинамической трубы с замкнутым контуром.

Рис. 12 Схема дозвуковой компрессорной аэродинамической трубы.

Рис. 13 Схема баллонной трансзвуковой эжекторной аэродинамической трубы

Рис. 14 Схема сверхзвуковой баллонной аэродинамической трубы

Рис. 15 Схема баллонной гиперзвуковой аэродинамической трубы

Источник

Жидкость, давление, скорость – основы закона сантехники

Главная страница » Жидкость, давление, скорость – основы закона сантехники

Сантехника, казалось бы, не даёт особого повода вникать в дебри технологий, механизмов, заниматься скрупулёзными расчётами для выстраивания сложнейших схем. Но такое видение – это поверхностный взгляд на сантехнику. Реальная сантехническая сфера ничуть не уступает по сложности процессов и, также как многие другие отрасли, требует профессионального подхода. В свою очередь профессионализм – это солидный багаж знаний, на которых основывается сантехника. Окунёмся же (пусть не слишком глубоко) в сантехнический учебный поток, дабы приблизиться на шаг к профессиональному статусу сантехника.

Закон Паскаля

Фундаментальная основа современной гидравлики сформировалась, когда Блезу Паскалю удалось обнаружить, что действие давления жидкости неизменно в любом направлении. Действие жидкостного давления направлено под прямым углом к площади поверхностей.

Если измерительное устройство (манометр) разместить под слоем жидкости на определенной глубине и направлять его чувствительный элемент в разные стороны, показания давления будут оставаться неизменными в любом положении манометра.

То есть давление жидкости никак не зависит от смены направления. Но давление жидкости на каждом уровне зависит от параметра глубины. Если измеритель давления перемещать ближе к поверхности жидкости, показания будут уменьшаться.

Соответственно, при погружении измеряемые показания будут увеличиваться. Причём в условиях удвоения глубины, параметр давления также удвоится.

Закон Паскаля наглядно демонстрирует действие давления воды в самых привычных условиях для современного быта

Отсюда логичный вывод: давление жидкости следует рассматривать прямо пропорциональной величиной для параметра глубины. В качестве примера рассмотрим прямоугольный контейнер размерами 10х10х10 см., который заполнен водой на 10 см глубины, что по объёмной составляющей будет равняться 10 см 3 жидкости.

Этот объём воды в 10 см 3 весит 1 кг. Используя имеющуюся информацию и уравнение для расчёта, несложно вычислить давление на дне контейнера. Например: вес столба воды высотой 10 см и площадью поперечного сечения 1 см 2 составляет 100 г (0,1 кг). Отсюда давление на 1 см 2 площади:

P = F / S = 100 / 1 = 100 Па (0,00099 атмосферы)

Если глубина столба воды утроится, вес уже будет составлять 3 * 0,1 = 300 г (0,3 кг), и давление, соответственно увеличится втрое. Таким образом, давление на любой глубине жидкости равноценно весу столба жидкости на этой глубине, поделённому на площадь поперечного сечения столба.

Давление водяного столба: 1 — стенка контейнера для жидкости; 2 — давление столба жидкости на донную часть сосуда; 3 — давление на основание контейнера; А, С — области давления на боковины; В — прямой водяной столб; Н — высота столба жидкости

Объем жидкости, создающей давление, называется гидравлический напор жидкости. Давление жидкости благодаря гидравлическому напору, также остаётся зависимым от плотности жидкости.

Сила тяжести

Гравитация — одна из четырех сил природы. Мощь гравитационной силы между двумя объектами зависит от массы этих объектов. Чем массивнее объекты, тем сильнее гравитационное притяжение.

Когда выливается вода из контейнера, гравитация Земли притягивает воду к земной поверхности. Можно наблюдать тот же самый эффект, если на разных высотах разместить два ведра воды и соединить их трубкой.

Достаточно задать ход жидкости в трубке из одного ведра в другой, после чего сработает сила гравитации, и процесс перелива продолжится самопроизвольно. Гравитация, приложенные силы и атмосферное давление являются статическими факторами, которые в равной степени относятся к жидкостям, находящимся в покое или в движении.

Силы инерции и трения являются динамическими факторами, которые действуют только на жидкости в движении. Математическая сумма силы тяжести, приложенной силы и атмосферного давления, представляет собой статическое давление, полученное в любой зоне жидкости и в любой момент времени.

Статическое давление

Статическое давление существует в дополнение к любым динамическим факторам, которые также могут присутствовать одновременно. Закон Паскаля гласит:

Давление, создаваемое жидкостью, действует равноценно по всем направлениям и под прямым углом к содержащимся поверхностям.

Это определение касается только жидкостей, находящихся в полном покое или практически недвижимых. Определение справедливо также только для факторов, составляющих статический гидравлический напор.

Очевидно: когда скорость движения становится фактором, в расчёт берётся направление. Сила, привязанная к скорости, также должна иметь направление. Поэтому закон Паскаля, как таковой, не применяется к динамическим факторам мощности потока жидкости.

Скорость движения потока зависит от многих факторов, включая послойное разделение жидкостной массы, а также сопротивление, создаваемое разными факторами

Динамические факторы инерции и трения привязаны к статическим факторам. Скоростной напор и потери давления привязаны к гидростатическому напору жидкости. Однако часть скоростного напора всегда может быть преобразована в статический напор.

Сила, которая может быть вызвана давлением или напором при работе с жидкостями, необходима, чтобы начать движение тела, если оно находится в состоянии покоя, и присутствует в той или иной форме, когда движение тела заблокировано.

Поэтому всякий раз, когда задана скорость движения жидкости, часть ее исходного статического напора используется для организации этой скорости, которая в дальнейшем существует уже как напорная скорость.

Объем и скорость потока

Объем жидкости, проходящей через определённую точку в заданное время, рассматривается как объем потока или расход. Объем потока обычно выражается литрами в минуту (л/мин) и связан с относительным давлением жидкости. Например, 10 литров в минуту при 2,7 атм.

Скорость потока (скорость жидкости) определяется как средняя скорость, при которой жидкость движется мимо заданной точки. Как правило, выражается метрами в секунду (м/с) или метрами в минуту (м/мин). Скорость потока является важным фактором при калибровке гидравлических линий.

Объём и скорость потока жидкости традиционно считаются «родственными» показателями. При одинаковом объёме передачи скорость может меняться в зависимости от сечения прохода

Объем и скорость потока часто рассматриваются одновременно. При прочих равных условиях (при неизменном объеме ввода), скорость потока возрастает по мере уменьшения сечения или размера трубы, и скорость потока снижается по мере увеличения сечения.

Так, замедление скорости потока отмечается в широких частях трубопроводов, а в узких местах, напротив, скорость увеличивается. При этом объем воды, проходящей через каждую из этих контрольных точек, остаётся неизменным.

Принцип Бернулли

Широко известный принцип Бернулли выстраивается на той логике, когда подъем (падение) давления текучей жидкости всегда сопровождается уменьшением (увеличением) скорости. И наоборот, увеличение (уменьшение) скорости жидкости приводит к уменьшению (увеличению) давления.

Этот принцип заложен в основе целого ряда привычных явлений сантехники. В качестве тривиального примера: принцип Бернулли «виновен» в том, что занавес душа «втягивается внутрь», когда пользователь включает воду.

Разность давлений снаружи и внутри вызывает силовое усилие на занавес душа. Этим силовым усилием занавес и втягивается внутрь.

Другим наглядным примером является флакон духов с распылителем, когда нажимом кнопки создаётся область низкого давления за счёт высокой скорости воздуха. А воздух увлекает за собой жидкость.

Принцип Бернулли для самолётного крыла: 1 — низкое давление; 2 — высокое давление; 3 — быстрое обтекание; 4 — медленное обтекание; 5 — крыло

Принцип Бернулли также показывает, почему окна в доме имеют свойства самопроизвольно разбиваться при ураганах. В таких случаях крайне высокая скорость воздуха за окном приводит к тому, что давление снаружи становится намного меньше давления внутри, где воздух остаётся практически без движения.

Существенная разница в силе попросту выталкивает окна наружу, что приводит к разрушению стекла. Поэтому когда приближается сильный ураган, по сути, следует открыть окна как можно шире, чтобы уравнять давление внутри и снаружи здания.

И ещё парочка примеров, когда действует принцип Бернулли: подъем самолёта с последующим полётом за счёт крыльев и движение «кривых шаров» в бейсболе.

В обоих случаях создаётся разница скорости проходящего воздуха мимо объекта сверху и снизу. Для крыльев самолета разница скорости создаётся движением закрылков, в бейсболе — наличием волнистой кромки.

Практика домашнего сантехника на видеоролике

Полезный для получения практики сантехники видеоролик ниже демонстрирует некоторые приёмы, которые в любой момент могут потребоваться потенциальному хозяину жилища. Рекомендуется просмотр этого видео для получения актуальной информации по сантехническим манипуляциям:

КРАТКИЙ БРИФИНГ

Источник