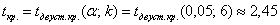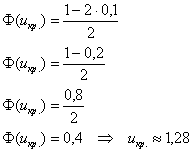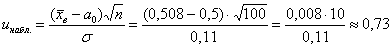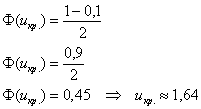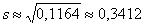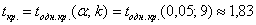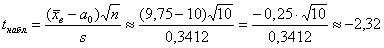Что такое статистическая гипотеза
11. Статистические гипотезы
Надо сказать, капитально я «подзавяз» в интегралах, диффурах и тервере, и после основательной доработки этих разделов безмерно рад напечатать первый абзац 11-й статьи по матстату.
Есть ли жизнь после сессии смерти? Далеко не каждая гипотеза является статистической, и перед тем как перейти к теме, я на всякий случай поставлю ссылку на 1-й урок по математической статистике, если «чайникам» будет что-то не понятно в терминах.
Сначала кратко разберём теорию, затем наиболее распространённые задачи (сразу ссылка для «самоваров»). Зажигаем:
Пусть исследуется некоторый признак статистической совокупности. Успеваемость студентов, продолжительность жизни… каждый подумал о своём, точность измерений, да что угодно – хоть качество помидоров. Всё, что можно «оцифровать» и посчитать.
Как проводится исследование? Обычно так: из генеральной совокупности извлекается репрезентативная выборка (всё понятно?), и на основании изучения этой выборки делается вывод обо всей совокупности. Напоминаю, что это основной метод математической статистики и называется он выборочным методом. В зависимости от исследования, могут проводиться неоднократные выборки, выборки из нескольких ген. совокупностей, да и вообще анализироваться произвольные статистические данные.
И в результате анализа этих данных появляются мысли, которые оформляются в статистические гипотезы.
Статистической называют гипотезу о законе распределения статистической совокупности либо о числовых параметрах известных (!) распределений.
– рост танкистов распределен нормально;
– дисперсии стрельбы двух танковых дивизий равны между собой, при этом известно*, что точность стрельбы распределена нормально.
* из многочисленных ранее проведённых исследований.
В первом случае выдвигается гипотеза о законе распределения, во втором – о числовых характеристиках двух распределений, закон которых известен.
Откуда взялись эти гипотезы? В первом случае была проведена выборка танкистов (например, 100 человек) и в результате её исследования появилось обоснованное предположение, что рост ВСЕХ танкистов распределён нормально. Во втором случае исследовались выборочные данные по точности стрельбы двух дивизий, в результате чего возник интерес проверить – а одинакова ли генеральная результативность, или же какая-то дивизия стреляет точнее?
В обеих гипотезах речь идёт о генеральных совокупностях, и выдвигаются эти гипотезы на основании анализа выборочных данных. Это распространенная схема, но она не единственна, бывают и другие статистические гипотезы.
Выдвигаемую гипотезу называют нулевой и обозначают через 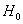
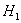
В рассмотренных выше примерах альтернативные гипотезы очевидны (отрицают нулевую), но существуют и другие варианты, так, например, к гипотезе 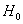
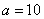
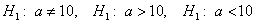
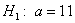
Поскольку нулевая гипотеза выдвигается на основании выборочных данных, то она может оказаться как правильной, так и неправильной – мы не знаем! И поэтому она подлежит статистической проверке.
Проверка осуществляется с помощью статистических критериев – это специальные случайные величины, которые принимают различные действительные значения. В разных задачах критерии разные, и мы рассмотрим их в конкретных примерах.
В результате проверки нулевая гипотеза либо принимается, либо отвергается в пользу альтернативной. При этом есть риск допустить ошибки двух типов:
Ошибка первого рода состоит в том, что гипотеза 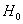
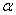
Ошибка второго рода состоит в том, что гипотеза 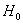
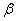
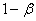
Уровень значимости задаётся исследователем самостоятельно, наиболее часто выбирают значения 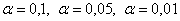
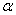
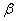
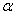
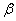
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я как раз приведу нестатистический пример…, опять напрашивается хардкор про диагностику болезни, но мы будем-таки настраиваться на позитив:
Танкист Вася поиграл с котами и зарегистрировался в почтовике. По умолчанию, 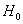
Какая ошибка более «тяжелая»? Васино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра целесообразно уменьшить уровень значимости 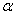
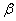
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность 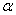
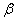
Ну а теперь возвращаемся к статистике.
Процесс проверки статистической гипотезы состоит из следующих этапов:
1) Обработка выборочных данных и выдвижение основной 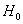
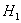
2) Выбор статистического критерия 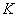
3) Выбор уровня значимости 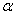
4) Нахождение критического значения 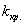
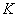
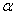
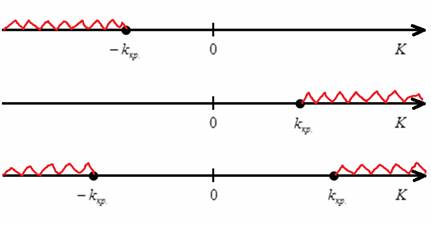
Критическая область – это область отвержения нулевой гипотезы. Незаштрихованную область называют областью принятия гипотезы.
Следует отметить, что это только одна из графических моделей. Существуют статистические критерии, которые принимают далеко не все действительные значения.
5) Далее на основании выборочных данных рассчитывается наблюдаемое значение критерия: 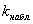
– Если 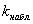
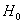
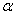
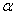
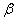
– Если 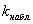
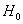
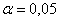
…ну а что делать? – такая вот статистика неточная наука 🙂
И по горячей информации сразу разберём одну из наиболее распространённых гипотез:
Гипотеза о генеральной средней нормального распределения
Постановка задачи такова: предполагается, что генеральная средняя 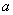
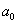
Для проверки гипотезы на уровне значимости 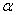
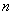
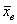
1) 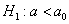
2) 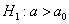
3) 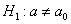
4) 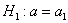
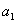
При этом возможны две принципиально разные ситуации:
а) если генеральная дисперсия  известна.
известна.
Тогда в качестве статистического критерия 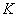
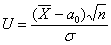
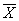
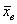
Далее находим критическую область. Для конкурирующих гипотез 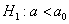
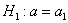
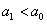
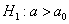
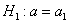
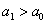
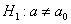
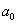
Чтобы найти критическую область нужно отыскать критическое значение 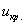
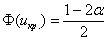
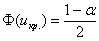
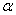
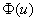
Теперь на основании выборочных данных рассчитываем наблюдаемое значение критерия: 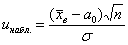
это можно было сделать и раньше, но такой порядок более последователен и логичен.
Результаты:
1) Для левосторонней критической области. Если 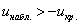
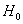
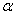
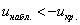
2) Правосторонняя критическая область. Если 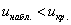
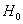
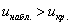
3) Двусторонняя критическая область. Если 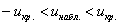
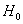

условие принятия гипотезы часто записывают компактно – с помощью модуля:
И немедленно приступаем к задачам, а то по студенческим меркам я тут уже на пол диссертации наговорил:)
Из нормальной генеральной совокупности с известной дисперсией 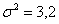
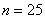
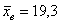
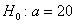
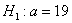
Прежде чем приступить к решению, пару слов о смысле такой задачи. Есть генеральная совокупность с известной дисперсией и есть веские основания полагать, что генеральная средняя равна 20 (нулевая гипотеза). В результате выборочной проверки получена выборочная средняя 19,3, и возникает вопрос: это результат случайный или же генеральная средняя и на самом деле меньше двадцати? – в частности, равна 19 (конкурирующая гипотеза).
Решение: по условию, известна генеральная дисперсия 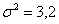
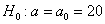
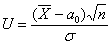
Найдём критическую область. Для этого нужно найти критическое значение. Так как конкурирующее значение 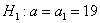
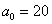
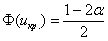
для уровня значимости 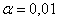
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что этому значению функции соответствует аргумент 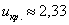
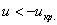
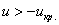
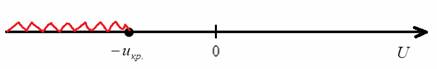
В данном случае 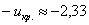
Вычислим наблюдаемое значение критерия:
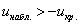
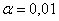
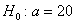
Такой, вроде бы неожиданный результат, объясняется тем, что генеральное стандартное отклонение достаточно великО: 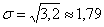
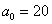
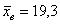
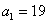
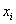
Ответ: на уровне значимости 0,01 нулевую гипотезу принимаем.
Что означает «на уровне значимости 0,01»? Это означает, что мы с 1%-ной вероятностью рисковали отвергнуть нулевую гипотезу, при условии, что она действительно справедлива. Однако не нужно забывать, что на самом деле она может быть и неверной и существует 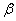
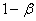
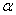
То была «обезличенная» задача, коих очень много, но мы будем менять мир к лучшему… физическими и химическими способами:) Заодно и понятнее будет, что здесь к чему:
По результатам 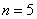
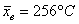
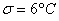
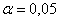
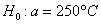
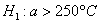
Сначала разберём, в чём жизненность этой ситуации. Есть печка. Для нормального технологического процесса нужна температура 250 градусов. Для проверки этой нормы 5 раз измерили температуру, получили 256 градусов. Из многократных предыдущих опытов известно, что среднеквадратическая погрешность измерений составляет 6 градусов (она обусловлена погрешностью самого термометра, случайными обстоятельствами проверки и т.д.)
И здесь не понятно, почему выборочный результат (256 градусов) получился больше нормы – то ли температура действительно выше и печь нуждается в регулировке, то ли это просто погрешность измерений, которую можно не принимать во внимание.
Решение: по условию, известно ген. среднее квадратическое отклонение 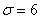
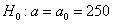
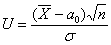
Найдём критическую область. Так как в конкурирующей гипотезе 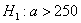
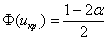
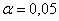
По таблице значений функции Лапласа или с помощью Калькулятора (Пункт 5*) определяем, что 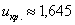
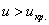
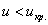
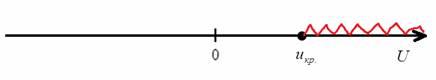
Вычислим наблюдаемое значение критерия:
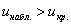
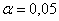
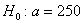
Как бы сказали статистики, выборочный результат 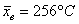
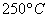
Ответ: на уровне значимости 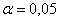
Ещё раз осмыслим – что означает «на уровне значимости 0,05»? Это означает, что с вероятностью 5% мы отвергли правильную гипотезу (совершили ошибку 1-го рода). И тут остаётся взвесить риск – насколько критично чуть-чуть уменьшить температуру (если мы всё-таки ошиблись и температура на самом деле в норме). Если даже небольшое уменьшение температуры недопустимо, то имеет смысл провести повторное, более качественное исследование: увеличить количество замеров 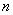
Следующая задача для самостоятельного решения, и на всякий случай я ещё раз продублирую ссылку на таблицу значений функции Лапласа и Калькулятор:
Средний вес таблетки сильнодействующего лекарства (номинал) должен быть равен 0,5 мг. Выборочная проверка 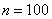
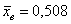
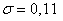
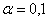
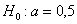
Рассмотрите как конкурирующую гипотезу 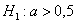
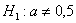
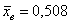
Краткое решение и ответы, как обычно, в конце урока.
Кстати, это тот самый пример, где ошибка 2-го рода (ошибочное принятие неверной нулевой гипотезы), может повлечь гораздо более тяжелые последствия (опасную передозировку). Поэтому в такой ситуации лучше включить паранойю и увеличить уровень значимости до 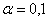
Можно ли одновременно уменьшить вероятности ошибок 1-го и 2-го рода ( 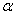
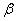
Теперь вторая ситуация. Та же самая задача, почти всё то же самое, но:
б) генеральная дисперсия  НЕ известна.
НЕ известна.
В этом случае остаётся ориентироваться на исправленную выборочную дисперсию 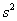
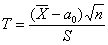
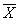
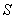
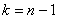
Алгоритм решения полностью сохраняется:
На основании 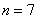
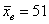
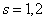
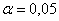
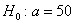
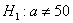
И начнём мы опять со смысла задачи, что здесь произошло? Здесь 7 раз измерили высоту этой камеры, получили среднее значение 51 мм и за неимением генеральной дисперсии вычислили исправленную выборочную дисперсию. Согласно норме, высота должна равняться 50 мм – эту гипотезу и проверяем.
Решение: так как генеральная дисперсия неизвестна, то для проверки гипотезы 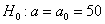
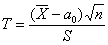
Конкурирующая гипотеза имеет вид 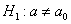
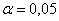
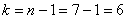
Таким образом, при 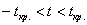
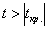
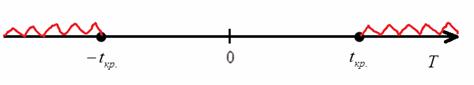
Вычислим наблюдаемое значение критерия:
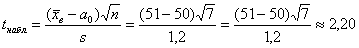
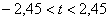
Ответ: на уровне значимости 0,05 гипотезу 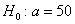
То есть, с точки зрения статистики, выборочный результат 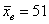
Творческая задача для самостоятельного решения:
Нормативный расход автомобильного двигателя составляет 10 л на 100 км. После конструктивных изменений, направленных на уменьшение этого показателя, были получены следующие результаты 10 тестовых заездов: 
На уровне значимости 0,05 выяснить, действительно ли расход топлива стал меньше.
Да, это не редкость – когда в предложенной задаче нужно не только проверить гипотезу, но и предварительно рассчитать выборочные значения. Кстати, даже при известной генеральной дисперсии, ориентироваться на неё тут нельзя, ибо конструктивные изменения могут изменить не только генеральную среднюю, но и генеральную дисперсию.
В лучших традициях курса все числа уже забиты в Эксель – там же инструкция по расчётам выборочных показателей. Если кто-то не знает или запамятовал, то вот ролик о том, как провести эти вычисления быстро (Ютуб).
В данной задаче критическая область левосторонняя, и критическое значение 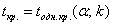
Постарайтесь грамотно оформить решение, свериться с образцом можно чуть ниже.
И я жду вас на следующем уроке, где мы продолжим проверять статистические гипотезы.
Пример 37. Решение: поскольку известно ген. стандартное отклонение, то для проверки гипотезы 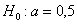
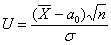
а) Рассмотрим конкурирующую гипотезу 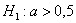
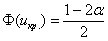
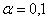
При 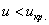
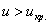
Вычислим наблюдаемое значение критерия:
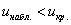
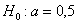
б) Рассмотрим конкурирующую гипотезу 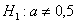
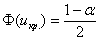
Для 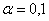
При 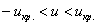
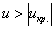

Наблюдаемое значение критерия 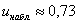
Ответ: в обоих случаях нулевую гипотезу на уровне значимости 0,1 принимаем.
Пример 39. Решение: вычислим сумму вариант 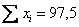
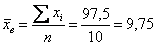
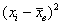
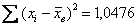
Вычисления удобно свести в таблицу: 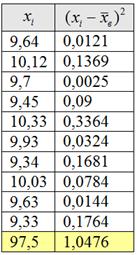
Выборочная дисперсия: 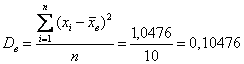
Исправленная выборочная дисперсия:
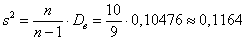
Исправленное стандартное отклонение.
На уровне значимости 0,05 проверим нулевую гипотезу 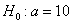
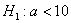
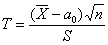
Найдём критическую область. Поскольку в конкурирующей гипотезе речь идёт о меньших значениях, то она будет левосторонней. Для уровня значимости 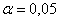
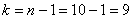
Таким образом, при 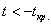
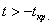
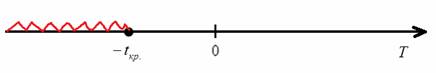
Вычислим наблюдаемое значение критерия:
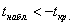
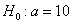
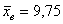
Ответ: на уровне значимости 0,05 можно утверждать, что расход топлива стал ниже.
Автор: Емелин Александр
(Переход на главную страницу)

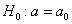
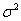 известна.
известна.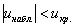
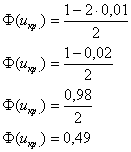
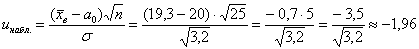
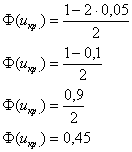
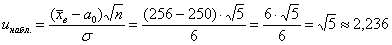
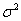 НЕ известна.
НЕ известна.