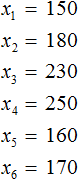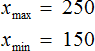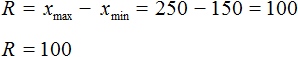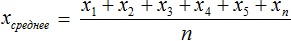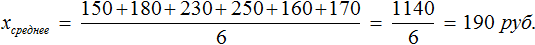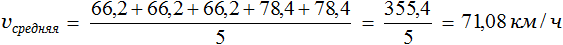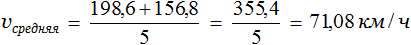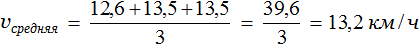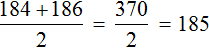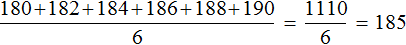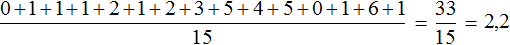Что такое статистика по алгебре 7 класс
Класс: 7
Презентация к уроку
Материальное обеспечение:
мультимедийный проектор, карточки для проведения самостоятельной работы.
ХОД УРОКА
1. Домашнее задание: п.9, №№ 168, 172, 178 (учебник «Алгебра. 7класс» под редакцией С. А. Теляковского, Москва «Просвещение», 2009 год)
2. Сообщение темы урока.
2.1. Разгадывание кроссворда:
2.2. – Прочитайте слово, образованное первыми буквами разгаданных слов. (Статистика)
– Как вы думаете, чем занимается статистика?
Статистика – это наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных явлениях, происходящих в природе и обществе. (Слайд 2)
Экономическая статистика изучает изменение цен, спроса и предложения на товары, прогнозирует спрос и падение производства и потребления.
Медицинская статистика изучает эффективность различных лекарств и методов лечения, вероятность возникновения некоторого заболевания в зависимости от возраста, пола, наследственности, условий жизни, вредных привычек, прогнозирует распространение эпидемий.
Демографическая статистика изучает рождаемость, численность населения, его состав (возрастной, национальный, профессиональный).
А ещё есть статистика финансовая, налоговая, биологическая, метеорологическая и т.д.
Для обработки информации существуют определённые методы. (Слайд 3)
Раздел математики, посвящённый методам и правилам обработки и анализа статистических данных, называется математической статистикой. (Слайд 4)
2.3. Сообщение темы урока.
– Сегодня мы будем знакомиться с некоторыми статистическими характеристиками, будем учиться их определять. (Слайд 5).
3. Изучение нового материала.
3.1. – Рассмотрим данные о производстве пшеницы в России в период с 1995 года по 2001 год. (Слайд 6)
1995 г. – 30,1 млн. тонн;
1996 г. – 34,9 млн. тонн;
1997 г. – 44,3 млн. тонн;
1998 г. – 27 млн. тонн;
1999 г. – 31 млн. тонн;
2000 г. – 34,5 млн. тонн;
2001 г. – 47 млн. тонн.
– Как видим, производство пшеницы в разные годы различается. Как вы думаете, почему?
– Да, оно зависит от погодных условий, площади посева, качества семян и других обстоятельств. Поэтому производство пшеницы за 1 год не даёт полного представления об уровне производства пшеницы в стране. Для этой цели лучше использовать среднее значение за ряд лет. По данным таблицы мы можем вычислить среднее производство пшеницы за 7 лет. Как это можно сделать?
(30,1 + 34,9 + 44,3 + 27 + 31 + 34,5 + 47) : 7 = 35,5 (Слайд 7)
– Что мы нашли? (Среднее арифметическое)
– Среднее арифметическое является одной из статистической характеристик ряда чисел. Запишите определение этого понятия в тетрадь. (Слайд 8)
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на их количество.
– В каком году производство пшеницы было ближе всего к среднему значению? (в 1996 году)
3.2. Выполните задания (слайд 9):
1) Вычислите среднее арифметическое чисел 6, 10, 16 и 20. (6 + 10 + 16 + 20) : 4 = 52 : 4 = 13
2) Все числа равны между собой. Чему рано их среднее арифметическое? (Самому этому числу.)
3) Может ли среднее арифметическое не совпадать ни с одним из чисел данного ряда? (Да)
4) Придумайте три числа, среднее арифметическое которых совпадает со вторым по величине числом.
3.3. В одном из седьмых классов измерили рост мальчиков. Получили такие данные:
155 см, 167 см, 159 см, 168 см, 161 см, 170 см, 162 см, 153 см, 165 см. (Слайд 10) Найдите среднее арифметическое этого ряда чисел.
(155 + 167 + 159 + 168 + 161 + 170 + 162 + 153 + 165) : 9 = 1460 : 9 = 162,(2) = 162
– Какой рост имеет самый высокий мальчик из этого класса? (170 см)
– Самый низкий мальчик? (153 см)
– Найдите разницу в росте ребят?
170 – 153 = 17 (см)
Разность между наибольшим и наименьшим значениями ряда данных называется размахом ряда и также является одной из статистических характеристик. (Слайд 11)
– Запишите определение в тетрадь.
3.4. Петя и Вася поспорили, кто лучше прыгает в длину с места. Чтобы избежать случайности, они решили, что будут прыгать по очереди 5 раз. (Слайд 12) Результаты своих прыжков они записали в таблицу (слайд 13):
Элементы статистики
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
Элементы выборки обозначаются с помощью переменных с индексами 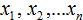
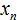
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
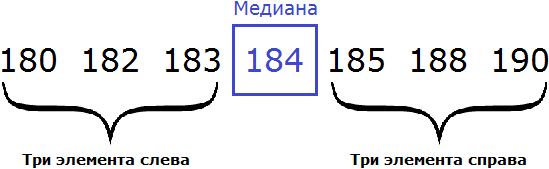
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
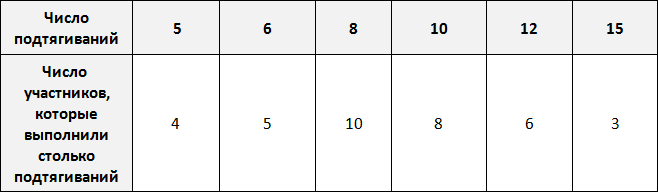
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
42 thoughts on “Элементы статистики”
Спасибо, что вы вернулись.
Будут ли новые уроки?
Разработка серии уроков по алгебре для 7-го класса по теме «Статистические характеристики»
Разделы: Математика
Урок 1. «Среднее арифметическое, размах и мода»
Тип урока: ознакомление с новым материалом.
Цели:
Оборудование: проектор.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
Слышали ли вы когда-нибудь такую песню: «Потому что на десять девчонок по статистике девять ребят»? Как вы думаете, что это значит?
Сегодня мы познакомимся с новой наукой – статистикой. Узнаем, что она изучает и как можно применить те знания, которые вы сейчас получите.
III. Актуализация знаний
– Какое число называют средним арифметическим нескольких чисел?
(Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых).
Задача: дан ряд чисел 5, 6, 8, 12, 15, 4, 17, 8, 10, 15.
IV. Первичное усвоение, осознание и осмысление нового материала
– Ребята, вы начинаете изучать новый предмет: «Элементы статистики и теории вероятностей».
– Где в реальной повседневной жизни мы сталкиваемся с этими науками?
– Вы что-нибудь слышали об этом разделе математики?
– А разве вам не приходилось подсчитывать среднюю скорость движения, средний бал ученика, класса. Подготовку человека к таким проблемам во всем мире осуществляет школьный курс математики, и в частности ее раздел «Математическая статистика».
Статистика – наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в природе и обществе. Слово «статистика» происходит от латинского слова status, которое означает «состояние, положение вещей». Статистика изучает численность отдельных групп населения страны и ее регионов, производство и потребление разнообразных видов продукции, перевозку грузов и пассажиров различными видами транспорта, природные ресурсы и многое другое. Результаты статистических исследований широко используются для практических и научных выводов. Вам было дано задание: измерить время, затраченное на выполнение домашнего задания по алгебре.
Мы получили следующие результаты: 27, 25, 26, 25, 40, 38, 38, 25 и т.д.
Имея этот ряд данных, можно определить, сколько минут в среднем затратили учащиеся на выполнение домашнего задания.
– Что для этого нужно сделать? (сложить все числа и разделить полученную сумму на их количество).
Число 28, полученное в результате, называют средним арифметическим рассматриваемого ряда. Обозначение: 
Мы вычислили, что на выполнение домашнего задания по алгебре учащиеся затратили в среднем 28 минут. Проводя аналогичные наблюдения, можно проследить, какова была средняя затрата времени на выполнение в какой-либо день домашнего задания по алгебре и русскому языку.
Заметим, что иногда вычисление среднего арифметического не дает полезной информации, так как время, затраченное некоторыми учащимися, значительно отличается от среднего арифметического.
Наибольший расход времени равен 40 минут, а наименьший расход времени равен 18 минут. Разность между наибольшим и наименьшим значением называется размахом ряда.
Размах ряда находят тогда, когда хотят определить, как велик разброс данных в ряду.
-Ребята, нас могут интересовать не только среднее арифметическое и размах, но и другие показатели.
Например, интересно знать, какое число встречается в ряду данных чаще всего.
Таким числом является число 25. Число, наиболее часто встречающееся в данном ряду, называется модой чисел.
Ряд может иметь две моды, а может не иметь моды. Например, 47, 46, 50, 52, 47, 49, 52, 55 – имеет две моды: 47 и 52.
69, 68, 66, 70, 67, 71, 74, 63, 73, 72 – этот ряд не имеет моды.
– Ребята, где еще можно встретить понятие моды ряда чисел?
– Данные о размерах мужских сорочек, проданных в определенный день в универмаге. Здесь мода – размер пользующихся спросом, мода – цены на товар распространенный на рынке и т.п.
V. Закрепление изученного материала
При выставлении оценок учитель также вычисляет среднее арифметическое ваших текущих оценок.
Сейчас вы получите выписку ваших оценок по алгебре за I четверть.
Вы должны вычислить среднее арифметическое, моду и размах.
VI. Подведение итогов урока
Выставление оценок за работу на уроке.
«В среднем в день ребёнок улыбается 400 раз, взрослый — 17. Теперь все улыбнулись, чтобы испортить статистику»
VIII. Рефлексия
Раздать карточки для рефлексии.
VII. Постановка домашнего задания п. 9, 168 (а, б), 172, 178
Урок 2. «Медиана как статистическая характеристика»
Тип урока: ознакомление с новым материалом.
Цели:
Оборудование: проектор
Ход урока
I. Организационный момент
II. Проверка домашнего задания
III. Сообщение темы и целей урока
Сегодня на уроке мы повторим алгоритм нахождения среднего арифметического, размаха и моды, и узнаем, как находится еще одна характеристика – медиана.
IV. Актуализация опорных знаний учащихся
1. Фронтальный опрос.
а) Дан ряд чисел: 3, 5, 1, 7, 9. Найти среднее арифметическое, размах и моду.
б) Дан ряд чисел: 1, 2, 2, 5, 5. Найти среднее арифметическое, размах и моду.
V. Первичное усвоение, осознание и осмысление нового материала
Задача. В небольшой фирме 10 сотрудников: 7 рабочих, мастер, бухгалтер, директор. Зарплата у рабочих: 2000, у мастера 4000, у бухгалтера 16000, у директора 40000. Найдите чему будет равна средняя зарплата на этом предприятии?
Но достаточно ли этой характеристики работнику, который устраивается работать рабочим? (Нет)
В этом случае используют другую статистическую характеристику – медиану.
Запишем алгоритм нахождения медианы набора чисел:
Медиану используют вместо средней арифметической, когда крайние варианты упорядоченного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.
VI. Закрепление изученного материала
Задача 2. В таблице приведена информация о длине основных рек, протекающих по территории округа Домодедово Московской области.
| Река | Длина, км |
| Пахра | 900 |
| Рожайка | 51 |
| Битца | 24 |
| Гнилуша | 31 |
| Северка | 98 |
| Конопелька | 13 |
а) Найдите среднюю длину рек (среднее арифметическое);
б) Найдите длину рек в среднем (медиану данных);
в) По вашему мнению, какая из этих характеристик – среднее арифметическое или медиана – лучше описывает длину рек, протекающих в Домодедовском районе? Ответ объясните.
Ответ: а) 186 км, б) 41 км, в) медиана, т.к. данные содержат значения сильно отличающиеся от всех прочих.
Итак, для характеристики статистической информации используют среднее арифметическое и медиану. Во многих случаях одна из характеристик может не иметь никакого содержательного смысла.
VI. Подведение итогов урока
У статистиков есть шутка: средняя глубина озера 0,5 м, а корова все-таки утонула. Как вы понимаете эту фразу?
Выставление оценок за работу на уроке.
VIII. Рефлексия
Раздать карточки для рефлексии.
VII. Постановка домашнего задания п.10, 187, 190, 193
Урок 3. «Статистические характеристики»
Тип урока: закрепление изученного.
Цели:
Оборудование: карточки для выполнения проверочной работы.
Ход урока
I. Организационный момент
II. Проверка домашнего задания, уточнение направлений актуализации материала
III. Сообщение темы, цели и задач урока, мотивация учения
Сегодня на уроке мы продолжим находить основные статистические характеристики числовых рядов.
IV. Воспроизведение изученного и их первичное применение в новых или измененных условиях с целью формирования умений
1. Фронтальный опрос
В таблице приведены расходы учащегося 7 класса за 4 дня:
| День | Понедельник | Вторник | Среда | Четверг |
| Расходы | 100 | 75 | 50 | 75 |
Определить какая статистическая характеристика находится в каждом задании:
б) 50, 75, 75, 100;
(75+75):2 = 75;
___=75 р.
в) 100, 75, 50, 75;
___=75 р.
3. Решение заданий повышенной сложности
V. Проверочная работа
Выдаются карточки с заданием. Эти карточки подписываются учащимися. Задания выполняются на этих карточках в течение 3-5 минут.
Ребята меняются карточками. И по готовым ответам на доске проверяют работы друг друга и выставляют отметки согласно предложенным критериям.
Оценка: «5» – всё верно; «4» – 3 задания выполнены верно; «3» – 2 задания выполнены верно; «2» – выполнено верно менее двух зданий.
Работы сдаются учителю для просмотра и анализа усвоения материала.
VI. Подведение итогов урока
Выставление оценок за урок.
VII. Рефлексия
Раздать карточки для рефлексии.
VIII. Постановка домашнего задания №182, №183, №193
Провести сбор информации на тему: «Размер обуви учеников 7 класса», «Рост учеников 7 класса», «Количество детей в семье учеников 7 класса» (в трех экземплярах)
Урок 4. «Статистические характеристики нашего класса»
Тип урока: обобщения и систематизации знаний.
Цели:
Оборудование: таблицы для заполнения данных.
Ход урока
I. Организационный момент
II. Сообщение темы и целей урока
– На перемене я собрала ответы на все ваши вопросы. Все готовы приступить к групповому исследованию. Начинаем заключительный урок по теме “Статистические характеристики”.
III. Воспроизведение и коррекция опорных знаний
IV. Обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий
Сегодня на уроке мы проведем с вами статистическое исследование.
Запишем основные этапы статистического исследования:
Рассмотрим следующую задачу:
В женском обувном магазине провели статистические исследования и составили соответствующую таблицу по цене обуви и количества продаж:
| Цена (руб.) | 500 | 1200 | 1500 | 1800 | 2000 | 2500 |
| Количество | 8 | 9 | 14 | 15 | 3 | 1 |
Первый и второй этап статистического исследования уже пройдены: данные собраны и систематизированы. Осталось произвести анализ данных.
Для данных показателей надо найти статистические характеристики и объяснить их значение. После ученики должны ответить на следующие вопросы:
По каким параметрам еще можно провести статистические исследования в обувном магазине?
V. Усвоение ведущих идей и основных теорий на основе широкой систематизации знаний
Проведем собственное статистическое исследование. У вас было домашнее задание: принести данные о своем росте, размере обуви и количестве детей в семье.
Сейчас каждый ряд получит свое задание :
Так как статистическое исследование состоит из трех этапов, а первый этап – сбор данных мы уже провели, то вы можете переходить ко второму этапу – систематизации данных. Для этого данные занесите в таблицы.
После того как вы провели систематизацию данных, можно переходить к следующему этапу – анализу данных. Найдите статистические характеристики: среднее арифметическую, моду, медиану и размах ряда. Сделайте выводы.
VI. Подведение итогов урока
Вы все отлично справились с заданием. Выставление оценок за работу на уроке.
VII. Постановка домашнего задания
Провести исследование на тему: «Рост учащихся 8 класса».