Что такое стационарные и критические точки функции

Критические точки функции

Рассмотрим следующий рисунок.

Максимум и минимум функции

В таком случае, точку х = 0 называют точкой максимума функции. По аналогии с этим, точку х = 2 называют точкой минимума функции y = x^3 – 3*x^2. Потому что существует такая окрестность этой точки, в которой значение в этой точке будет минимальным среди всех других значений из этой окрестности.

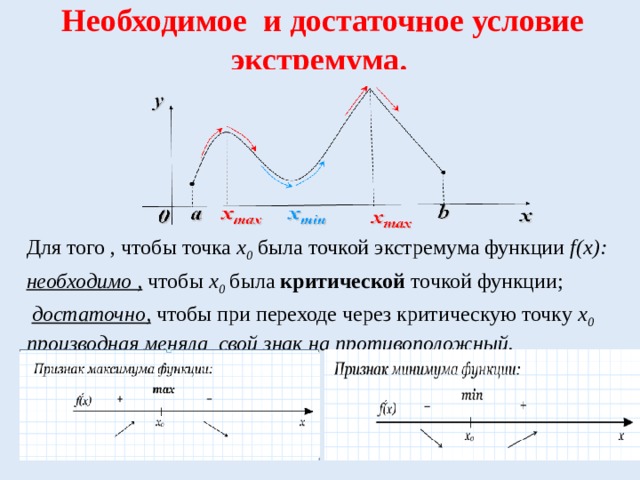
Точкой максимума функции f(x) называется точка x0, при условии, что существует окрестность точки х0 такая, что для всех х не равных х0 из этой окрестности, выполняется неравенство f(x) f(x0).

В точках максимума и минимума функций значение производной функции равно нулю. Но это не достаточное условие для существования в точке максимума или минимума функции.

Например, функция y = x^3 в точке х = 0 имеет производную равную нулю. Но точка х = 0 не является точкой минимума или максимума функции. Как известно функция y = x^3 возрастает на всей числовой оси.

Таким образом, точки минимума и максимума всегда будут находиться среди корне уравнения f’(x) = 0. Но не все корни этого уравнения будут являться точками максимума или минимума.

Стационарные и критические точки

Точки, в которых значение производной функции равно нулю, называются стационарными точками. Точки максимума или минимума могут иметься и вточках, в которых производной у функции вообще не существует. Например, у = |x| в точке х = 0 имеет минимум, но производной в этой точке не существует. Эта точка будет являться критической точкой функции.

Критическими точками функции называются точки, в которых производная равна нулю, либо производной в этой точке не существует, то есть функция в этой точке недифференцируема. Для того чтобы найти максимум или минимум функции необходимо выполнение достаточного условия.

Пусть f(x) некоторая дифференцируемая на интервале (a;b) функция. Точка х0 принадлежит этому интервалу и f’(x0) = 0. Тогда:

1. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «плюса» на «минус», тогда точка х0 является точкой максимума функции.

2. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «минуса» на «плюс», тогда точка х0 является точкой минимума функции.

Источник

Что такое стационарные и критические точки функции

Определения:

Экстремумом называют максимальное или минимальное значение функции на заданном множестве.

Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.

Точка максимума – это точка, в которой достигается максимальное значение функции.

Точка минимума – это точка, в которой достигается минимальное значение функции.

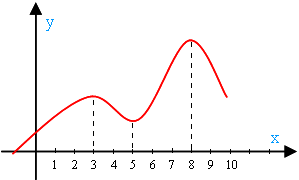
На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:

В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:

Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.

Точка x_о является точкой максимума, если у нее существует окрестность, во всех точках которой f(x) меньше или равно f(x_о):

Упрощенная формулировка : если в точке x_о производная меняет знак с плюса на минус, то x_о является точкой максимума.

Точка х_о является точкой минимума, если у нее существует окрестность, во всех точках которой f(x) больше или равно f(x_о):

Упрощенная формулировка : если в точке x_о производная меняет знак с минуса на плюс, то x_о является точкой минимума.

Критические и стационарные точки функции:

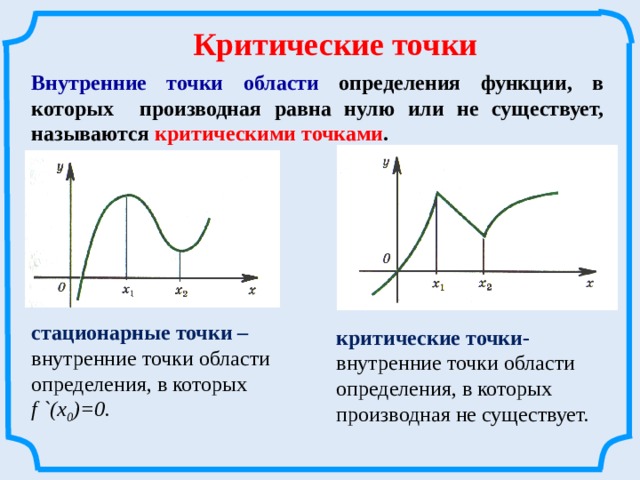
Внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, называют критическими точками.

Внутренние точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.

Необходимое условие экстремума:

Если x_о – точка экстремума функции f (x), то в этой точке либо производная обращается в нуль (и это стационарная точка), либо производная не существует (критическая точка).

Достаточное условие экстремума:

Пусть x_о – критическая точка. Если производная f ′(x) при переходе слева направо через точку x_о меняет знак плюс на минус, то x_о – точка максимума:

Если производная f ′(x) при переходе слева направо через точку x_о меняет знак минус на плюс, то x_о – точка минимума:

Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:

2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x).

3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.

4) Сделать выводы о монотонности функции и ее точках экстремума.

Источник

Понятие экстремума функции

Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.

Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.

Необходимое условие экстремума

(Необходимое условие экстремума)

Не в каждой своей критической точке функция обязательно имеет максимум или минимум.

Первое достаточное условие экстремума

(Первое достаточное условие экстремума)

Решение. Находим производную заданной функции:

Второе достаточное условие экстремума

(Второе достаточное условие экстремума)

Понятие экстремума функции не по зубам? Тебе ответит эксперт через 10 минут!

Решение. Находим первую производную заданной функции:

Находим точки, в которых первая производная равна нулю:

Вторая производная заданной функции:

Остались вопросы?

Здесь вы найдете ответы.

Экстремум представляет собой значение функции на определенном интервале в момент достижения им минимального или максимального показания. Под понятием «экстремумы» или по-другому минимумы/максимумы подразумевается значение функции (у).

Если в определенной точке достигается экстремум или, иными словами, максимальное/минимальное значение функции на заданном интервале, то эта точка носит название точки экстремума. Из этого следует, что при достижении минимума, точка экстремума будет названа точкой минимума, и, наоборот, при достижении максимума эта точка будет называться точкой максимума. В случае, когда указываются точки экстремумов (или минимумов/максимумов) подразумеваются иксы, в которых достигаются минимальные или максимальные значения.

Под понятием «минимум функции» имеется в виду та точка на ней, в которой функция имеет значение, являющееся наименьшим среди всех значений, приобретаемых ею в любой из других соседних точек. Другими словами, это означает, что в случае, когда функция, достигнув определенной точки, прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и представляет собой точку ее минимума.

Для ответа на поставленный вопрос нужно отыскать точку минимума указанной функции, в которой ее значение перестает падать. Это можно сделать следующим образом:

Предположив, что минимальное значение данной функции равно 0, можно переписать равенство в следующем виде:

Сократим данное уравнение на 4:

Получившееся равенство также может быть записано в следующем виде после перемены местами слагаемых:

Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:

Это же уравнение может выглядеть так:

Теперь для упрощения можно переписать уравнение в таком виде:

В этом случае х = 1

Знаками «+» и «-» обозначены значения производной.

После проведенных вычислений было установлено, что х = 1, что является точкой минимума функции:

Точкой максимума называется то значение х, достигнув которого, производная начинает менять свой знак с плюса на минус. Зная это, можно перейти к поиску точки максимума для функции, указанной в задании.

Для этого нужно начать с поиска производной, используя следующую формулу:

Подставляем приведенные в задании значения и получаем:

Теперь следует приравнять производную к 0 и начать решать получившееся уравнение:

Упростим уравнение и получим:

Избавимся от минусов в уравнении:

Отсюда следует, что:

Можно сделать вывод о том, что х = 1,5.

Запишем производную данной функции:

А затем приравняем ее к 0:

Это позволяет сделать вывод о том, что:

Получается, что, если x 3/2, то производная y’ > 0, и в этом случае функция возрастает.

x =3/2=1,5 – это единственная точка экстремума, которая является точкой минимума.

Критическая точка функции представляет собой ту точку, при пересечении с которой производная данной функции становится равной 0, либо она вовсе не существует.

Для начала нужно определить, что под критической точкой функции подразумевается та точка, при пересечении с которой производная приобретает нулевое значение, либо же эта производная просто не существует в этой точке, что означает, что функцию в данной точке невозможно дифференцировать.

Проверим, применимо ли это утверждение к упомянутой в задании функции:

Приравняем производную функции к 0:

f ‘(x) = 0, это значит, что 2sin2x-3 = 0.

sin2x= 3 2 не имеет решения

Ответ: заданная функция не имеет критических точек и существует при любых х.

Под критическими точками функции понимаются те точки, в которых ее производная равна 0 или вовсе не существует.

Источник

КРИТИЧЕСКИЕ ТОЧКИ И ЭКСТРЕМУМЫ ФУНКЦИИ

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

10.03.17 Классная работа Критические точки и экстремумы функции

Найти значения х, при которых значение f(x) равно 0

y = f ´(х) По графику производной функции определите, на каких промежутках функция возрастает, на каких убывает.

x y O x0 Точка максимума x0+ x0- x y(x0) y(x)

x O x0 Точка минимума y(x0) y Сформулируйте определение самостоятельно y(х) > y(x0) y(x) x

Точки максимума и минимума называются точками экстремума функции

Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками. Критические точки

Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта точка была критической точкой данной функции Но это условие не является достаточным

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-264040

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Ученые изучили проблемы родителей, чьи дети учатся в госпитальных школах

Время чтения: 5 минут

Российские юниоры завоевали 6 медалей на Международной научной олимпиаде

Время чтения: 2 минуты

В российских школах могут появиться «службы примирения»

Время чтения: 1 минута

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Критические точки, точки экстремумафункции

Содержимое разработки

Специализированная гимназия № 8 с обучением на трех языках имени М.Х. Дулати

Алгебра и начала анализа

Критические точки и

Л.С. Атанасян. Геометрия 10-11

Харченко Татьяна Викторовна

— знать определения критических точек и точек экстремума функции, условие существования экстремума функции.

Л.С. Атанасян. Геометрия 10-11

— Использует определение находит критические (стационарные) точки, используя определение;

— применяет необходимое и достаточное условие для определение точек экстремума функции.

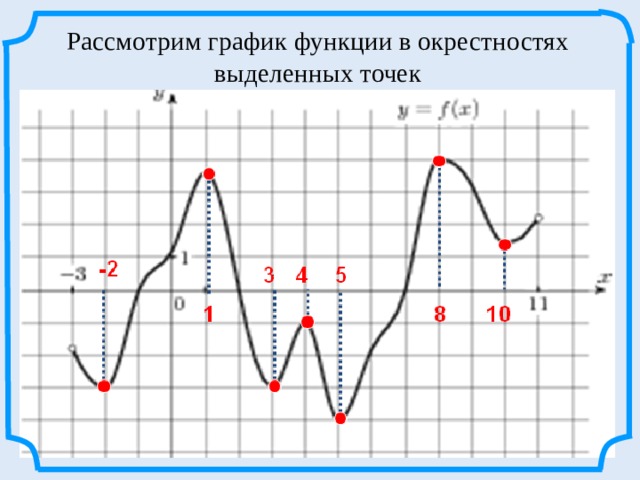
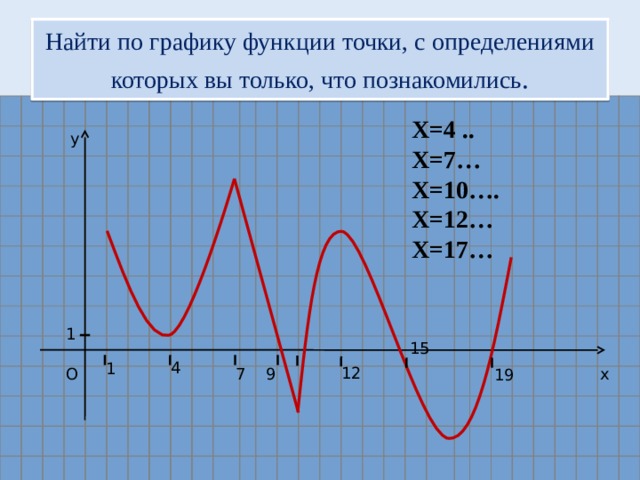
Рассмотрим график функции в окрестностях выделенных точек

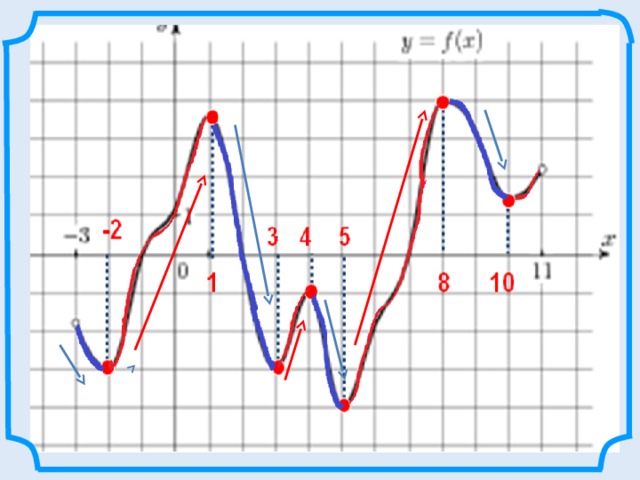
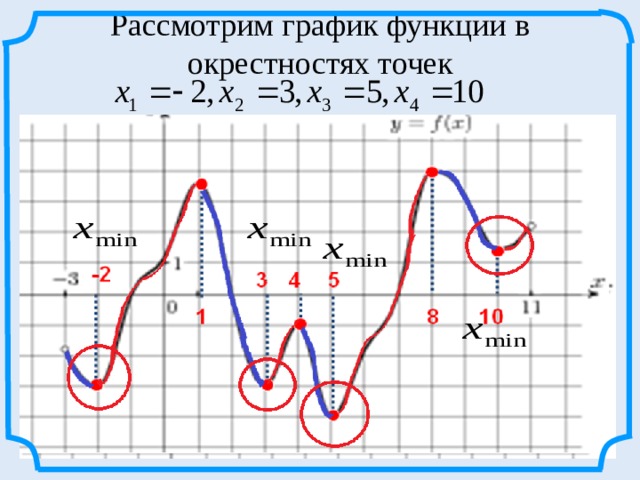
Рассмотрим график функции в окрестностях точек

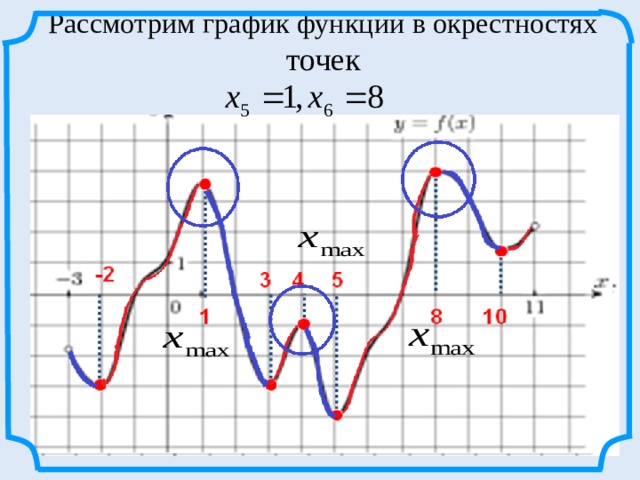
Рассмотрим график функции в окрестностях точек

f( х 0 ) » width=»640″

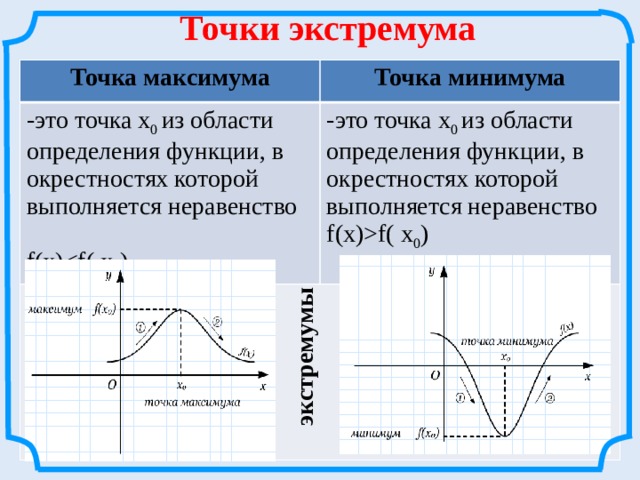
-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство

-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство f(x)f( х 0 )

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками .

внутренние точки области

определения, в которых f `(х 0 )=0.

критические точки- внутренние точки области

определения, в которых производная не существует.

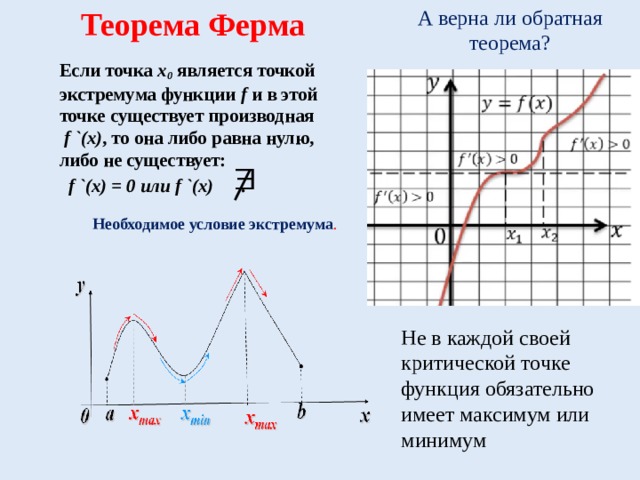
А верна ли обратная теорема?

Если точка х 0 является точкой экстремума функции f и в этой точке существует производная f `(x) , то она либо равна нулю, либо не существует:

Необходимое условие экстремума .

Не в каждой своей критической точке функция обязательно имеет максимум или минимум

Достаточные условия существования экстремума в точке

Признак максимума функции.

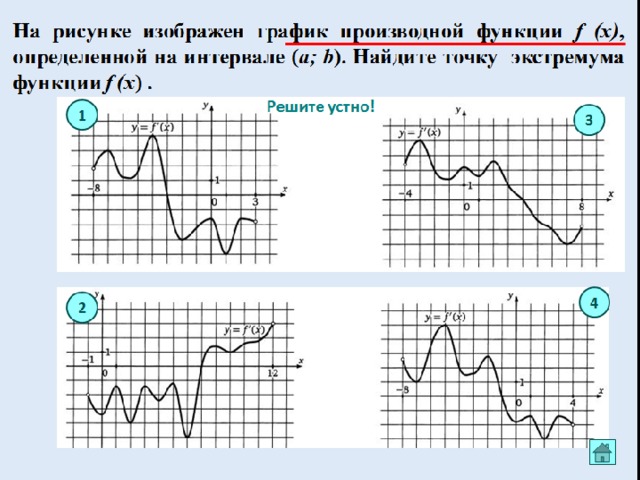
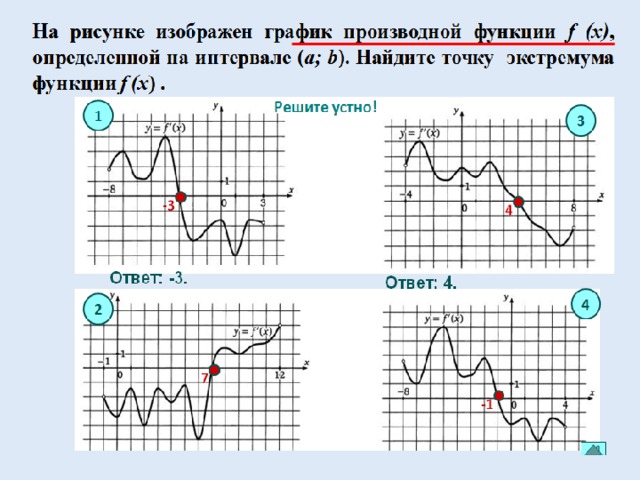
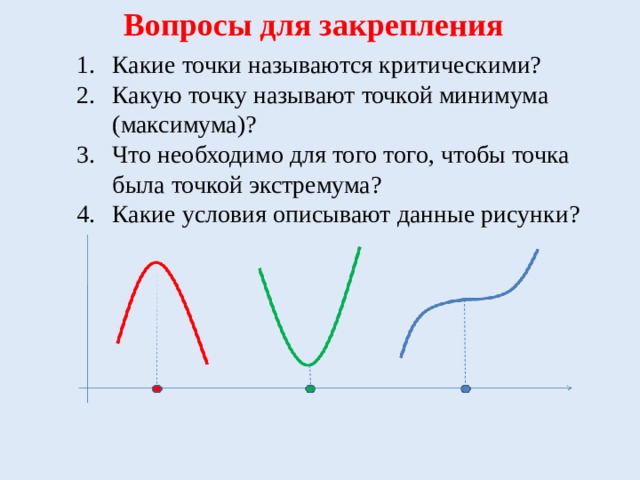
Вопросы для закрепления

Необходимое и достаточное условие экстремума.

достаточно, чтобы при переходе через критическую точку х 0 производная меняла свой знак на противоположный.

Найдите точку минимума функции

Найдите точку максимума функции

Задания для самостоятельного решения

1А. (5б) Найдите критические точки функции. Выясните, какие из этих точек являются:

а) точками минимума; б) точками максимума.

Находит правильно производную

Находит критические точки

Расставляет верно знаки производной

Определяет точки минимума

Определяет точки максимума

Задания для самостоятельного решения

2Б. (6б) Найдите экстремумы функции:

Находит область определения

Находит правильно производную

Находит критические точки

Расставляет верно знаки производной

Определяет точки экстремума

Находит экстремумы функции

Задания для самостоятельного решения

3С.(7б)Найдите промежутки возрастания и убывания, точки экстремума функции:

Находит область определения

Находит критические точки

Расставляет знаки производной

Исследует поведение функции

Находит промежутки монотонности

Определяет точки экстремума

Дополнительные цифровые ресурсы

Ссылки на дополнительные ресурсы для самообразования

https:// bilimland.kz /ru/subject/algebra/10-klass/kriticheskie-tochki-dostatochnoe-uslovie-sushestvovaniya-ehkstremuma?mid=%info%

https:// www.yaklass.ru/ p/algebra/10-klass/proizvodnaia-9147/primenenie-proizvodnoi-dlia-issledovaniia-funktcii-na-monotonnost-i-ekstr_-11226

Рефлексия содержания учебного материала

Дорогие дети! Вы получили самое основное содержание по новой теме, другие материалы вы получите от своего учителя! Если у вас есть вопросы, вы их можете задать учителю! Удачи в освоении нового материала, наши юные друзья!

Источник