Что такое стационарные и критические точки
Критические точки функции
Рассмотрим следующий рисунок.
Максимум и минимум функции
В таком случае, точку х = 0 называют точкой максимума функции. По аналогии с этим, точку х = 2 называют точкой минимума функции y = x^3 – 3*x^2. Потому что существует такая окрестность этой точки, в которой значение в этой точке будет минимальным среди всех других значений из этой окрестности.
Точкой максимума функции f(x) называется точка x0, при условии, что существует окрестность точки х0 такая, что для всех х не равных х0 из этой окрестности, выполняется неравенство f(x) f(x0).
В точках максимума и минимума функций значение производной функции равно нулю. Но это не достаточное условие для существования в точке максимума или минимума функции.
Например, функция y = x^3 в точке х = 0 имеет производную равную нулю. Но точка х = 0 не является точкой минимума или максимума функции. Как известно функция y = x^3 возрастает на всей числовой оси.
Таким образом, точки минимума и максимума всегда будут находиться среди корне уравнения f’(x) = 0. Но не все корни этого уравнения будут являться точками максимума или минимума.
Стационарные и критические точки
Точки, в которых значение производной функции равно нулю, называются стационарными точками. Точки максимума или минимума могут иметься и вточках, в которых производной у функции вообще не существует. Например, у = |x| в точке х = 0 имеет минимум, но производной в этой точке не существует. Эта точка будет являться критической точкой функции.
Критическими точками функции называются точки, в которых производная равна нулю, либо производной в этой точке не существует, то есть функция в этой точке недифференцируема. Для того чтобы найти максимум или минимум функции необходимо выполнение достаточного условия.
Пусть f(x) некоторая дифференцируемая на интервале (a;b) функция. Точка х0 принадлежит этому интервалу и f’(x0) = 0. Тогда:
1. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «плюса» на «минус», тогда точка х0 является точкой максимума функции.
2. если при переходе через стационарную точку х0 функция f(x) и её производная меняет знак, с «минуса» на «плюс», тогда точка х0 является точкой минимума функции.
Что такое стационарные и критические точки
Определения:
Экстремумом называют максимальное или минимальное значение функции на заданном множестве.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Точка максимума – это точка, в которой достигается максимальное значение функции.
Точка минимума – это точка, в которой достигается минимальное значение функции.
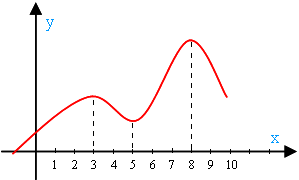
На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:
В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:
Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.
Точка xо является точкой максимума, если у нее существует окрестность, во всех точках которой f(x) меньше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с плюса на минус, то xо является точкой максимума.
Точка хо является точкой минимума, если у нее существует окрестность, во всех точках которой f(x) больше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с минуса на плюс, то xо является точкой минимума.
Критические и стационарные точки функции:
Внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, называют критическими точками.
Внутренние точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.
Необходимое условие экстремума:
Если xо – точка экстремума функции f (x), то в этой точке либо производная обращается в нуль (и это стационарная точка), либо производная не существует (критическая точка).
Достаточное условие экстремума:
Пусть xо – критическая точка. Если производная f ′(x) при переходе слева направо через точку xо меняет знак плюс на минус, то xо – точка максимума:
Если производная f ′(x) при переходе слева направо через точку xо меняет знак минус на плюс, то xо – точка минимума:
Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:
2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x).
3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4) Сделать выводы о монотонности функции и ее точках экстремума.
Стационарные критические и точки экстремума
Определения:
Экстремумом называют максимальное или минимальное значение функции на заданном множестве.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Точка максимума – это точка, в которой достигается максимальное значение функции.
Точка минимума – это точка, в которой достигается минимальное значение функции.
На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:
В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:
Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.
Точка xо является точкой максимума, если у нее существует окрестность, во всех точках которой f(x) меньше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с плюса на минус, то xо является точкой максимума.
Точка хо является точкой минимума, если у нее существует окрестность, во всех точках которой f(x) больше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с минуса на плюс, то xо является точкой минимума.
Критические и стационарные точки функции:
Внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, называют критическими точками.
Внутренние точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.
Необходимое условие экстремума:
Если xо – точка экстремума функции f (x), то в этой точке либо производная обращается в нуль (и это стационарная точка), либо производная не существует (критическая точка).
Достаточное условие экстремума:
Пусть xо – критическая точка. Если производная f ′(x) при переходе слева направо через точку xо меняет знак плюс на минус, то xо – точка максимума:
Если производная f ′(x) при переходе слева направо через точку xо меняет знак минус на плюс, то xо – точка минимума:
Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:
2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x).
3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4) Сделать выводы о монотонности функции и ее точках экстремума.
Определение
Точка 
называется точкой локального максимума функции 
, если существует такая окрестность этой точки, что для всех 
из этой окрестности выполняется неравенство: 
.
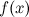
Точка называется точкой локального минимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности 
.
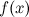
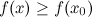
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума –локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка называется точкой строгого локального максимума функции 
, если для всех из окрестности этой точки будет справедливо строгое неравенство 
.
Точка называется точкой строгого локального минимума функции , если для всех из окрестности этой точки будет справедливо строгое неравенство 
.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция имеет экстремум в точке , то ее производная 
либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: 
, называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки – это либо стационарные точки (решения уравнения ), либо это точки, в которых производная 
не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции выполнены следующие условия:
1. функция непрерывна в окрестности точки ;
2. 
или не существует;
3. производная при переходе через точку меняет свой знак.
Тогда в точке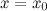 
функция имеет экстремум, причем это минимум, если при переходе через точку производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку производная меняет свой знак с плюса на минус.
Если производная при переходе через точку не меняет знак, то экстремума в точке нет.
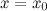
Таким образом, для того чтобы исследовать функцию на экстремум, необходимо:
1. найти производную ;
2. найти критические точки, то есть такие значения , в которых или не существует;
3. исследовать знак производной слева и справа от каждой критической точки;
4. найти значение функции в экстремальных точках.
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть для функции выполнены следующие условия:
1. она непрерывна в окрестности точки ;
2. первая производная в точке ;
3. 
в точке .
Тогда в точке достигается экстремум, причем, если 
, то в точке функция имеет минимум; если 
, то в точке функция достигает максимум.
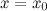
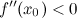
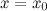
Выпуклость и точки перегиба. Основные понятия и определения. Достаточное условие выпуклости функции.
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.
На рисунке показана иллюстрация приведенного выше определения.
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).
Доказательство. Пусть х Î (a, b). Проведем касательную к кривой в этой точке.
Уравнение кривой: y = f(x);
Уравнение касательной: 
Следует доказать, что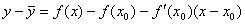 
.
По теореме Лагранжа для f(x) – f(x ):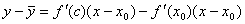 
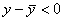
, x x тогда x 0 и c – x > 0, и кроме того по условию
, следовательно, 
.
Пусть x 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Доказательство. 1) Пусть f¢¢(x) 0 при x > a. Тогда при
x a кривая вогнута, т.е. точка х = а – точка перегиба.
2) Пусть f¢¢(x) > 0 при x b – выпуклостью вверх. Тогда x = b – точка перегиба.
Описание презентации по отдельным слайдам:
10.03.17 Классная работа Критические точки и экстремумы функции
Найти значения х, при которых значение f(x) равно 0
x y O 1 1 4 7 9 12 15 19 По графику функции определите, на каких промежутках производная функции положительна, на каких – отрицательна? у = f ( x )
y = f ´(х) По графику производной функции определите, на каких промежутках функция возрастает, на каких убывает.
x y O x0 Точка максимума x0+ x0- x y(x0) y(x)
x O x0 Точка минимума y(x0) y Сформулируйте определение самостоятельно y(х) > y(x0) y(x) x
Точки максимума и минимума называются точками экстремума функции
Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками. Критические точки
Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта точка была критической точкой данной функции Но это условие не является достаточным
Алгоритм нахождения точек экстремума: Найти производную функции. Решить уравнение f ´(х)=0, и найти тем самым стационарные точки. Методом интервалов установить промежутки знакопостоянства производной. Если при переходе через точку х0: – производная не меняет знак, то х0 – точка перегиба; – производная меняет знак с «+» на «-», то х0 точка максимума; – производная меняет знак с «-» на «+», то х0 точка минимума.
Номер материала: ДБ-264040
- 28.11.2018 1371
- 28.11.2018 104
- 28.11.2018 566
- 28.11.2018 178
- 28.11.2018 2458
- 28.11.2018 93
- 28.11.2018 147
- 28.11.2018 190
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.