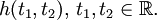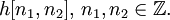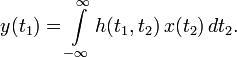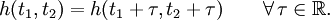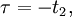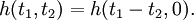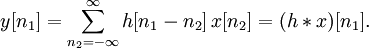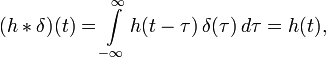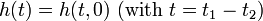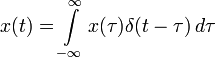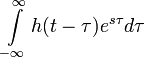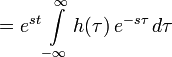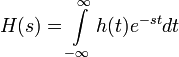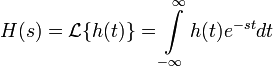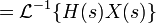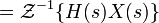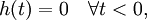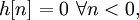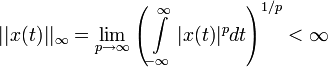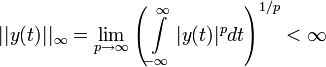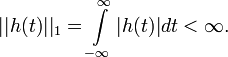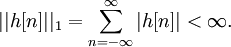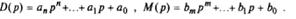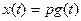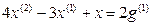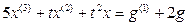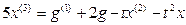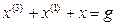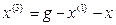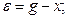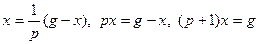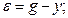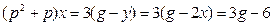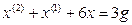Что такое стационарные системы
Линейная стационарная система
Теория линейных стационарных систем — раздел теории динамических систем, изучающая поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и других областях инженерного дела.
Содержание
Обзор
Определяющими свойствами для любой линейной стационарной системы являются линейность и стационарность:
Динамика систем, обладающих вышеперечисленными свойствами, может описываться одной простой функцией, к примеру, импульсной переходной функцией. Выход системы может рассчитываться как свёртка входного сигнала с импульсной переходной функцией системы. Этот метод анализа иногда называется анализом во временной области. Сказанное справедливо и для дискретных систем.
Кроме того, любая ЛСС может быть описана в частотной области с помощью своей передаточной функции, которая является преобразование Лапласа импульсной передаточной функции (или Z-преобразованием в случае дискретных систем). В силу свойств этих преобразований, выход системы в частотной области будет равен произведения передаточной функции и соответсвующего преобразования входного сигнала. Другими словами, свёртке во временной области соответсвует умножение в частотной области.
Так как синусоиды представляют собой сумму компелксных экспонент с комплексно-сопряжёнными частотами, если вход системы — синусоида, то выходом системы будет также синусоида, в общем случае с другой амплитудой и фазой, но с той же частотой.
Теория ЛСС хорошо подходит для описания многих систем. Большинство ЛСС гораздо проще анализировать, чем нестационарные и нелинейные системы. Любая система, динамика которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является линейной стационарной системой. Примерами таких систем являются электрические схемы, собранные из резисторов, конденсаторов и катушек индуктивности (RLC-цепочки). Груз на пружинке также можно считать ЛСС.
Большая часть общих концепций ЛСС схожа как в случае непрерывных систем, так и в случае дискретных систем.
Стационарность и линейные преобразования
Для дискретной системы:
Так как 
Если линейный оператор 
Для краткости записи второй аргумент в h(t1,t2) обычно опускается и интеграл суперпозиции становится интегралом свёртки:
Таким образом, интеграл свёртки показывает как линейная стационарная система отрабатывает любой входной сигнал. Полученное соотношение для дискретных систем:
Импульсная переходная функция
Если ко входу системы приложить входной сигнал в виде дельта-функции Дирака, результирующий выходной сигнал ЛСС будет представлять собой импульсную переходную функцию системы. Запись:
Для дискретной системы:
(из-за свойства сдвига дельта-функции).
то есть h(t) — импульсная переходная функция системы
Импульсная переходная функция используется для того, чтобы найти выходной сигнал системы как реакцию на любой входной сигнал. Кроме того, любой вход может быть представлен в виде суперпозиции дельта-функций:
Приложив ко входу системы, получим:
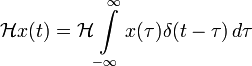
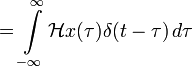
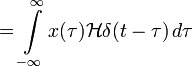
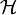
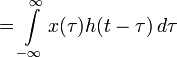
В импульсной переходной функции h(t) содержится вся информация о динамике ЛСС.
Собственные функции
Собственная функция — функция, для которой выход оператора представляет собой ту же функцию, в общем случае с точностью до постоянного множителя. Запись:
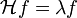
где f — собственная функция, и λ — собственное число, константа.
что эквивалентно следующему выражению в силу коммутативности свёртки:
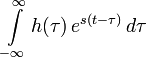
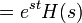
зависит только от s.
Таким образом, e st — собственная функция ЛСС.
Преобразования Лапласа и Фурье
Преобразование Лапласа обычно используется для односторонних сигналов, то есть при нулевых начальных условиях. Начальный момент времени без потери общности принимается за ноль, а преобразование берётся от ноля до бесконечности (преобразование, которое получается при интегрировании также и до минус бесконечности, называется двустороннее преобразование Лапласа).
Преобразование Фурье используется для анализа систем, через которые проходят периодические сигналы, и во многих других случаях — например, для анализа системы на устойчивость.
Из-за свойств свёртки для обоих преобразований имеют место следующие соотношения:
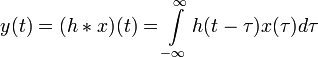
Для дискретных систем:
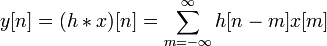
Некоторые свойства
Некоторые из важных свойств любой системы — причинность и устойчивость. Для того, чтобы система существовала в реальном мире, должен выполняться принцип причинности. Неустойчивые системы могут быть построены и иногда быть даже полезными.
Причинность
Система называется причинной, если её выход зависит только от текущего или предыдущего приложенного воздействия. Необходимое и достаточное условие причинности:
Для дискретных систем:
где h(t) — импульсная переходная функция. В явном виде определить причинная система или нет из её преобразования Лапласа в общем случае невозможно, так как обратное преобразование Лапласа не является уникальным. Причинность может быть определена когда задана область сходимости.
Устойчивость
Система является устойчивой по ограниченному входу, ограниченному выходу (англ. bounded input, bounded output stable, BIBO stable ) если для каждого ограниченного входа выходной сигнал является конечным. Запись: Если
Для дискретных систем:
См. также
Ссылки
Статьи, связанные с теорией управления и моделированием
динамических систем
Полезное
Смотреть что такое «Линейная стационарная система» в других словарях:
Теория линейных стационарных систем — раздел теории динамических систем, изучающий поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и других областях инженерного дела.… … Википедия
ЛСС — Теория линейных стационарных систем раздел теории динамических систем, изучающая поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и … Википедия
ЛСС — Латвийский союз самоуправлений Латвия Источник: http://www.regnum.ru/news/304683.html ЛСС линейные сооружения связи воен., связь Источник: http://www.rksi.ru/dopo/programs.shtml ЛСС летучее сернистое соединение … Словарь сокращений и аббревиатур
ГОСТ Р 53953-2010: Электросвязь железнодорожная. Термины и определения — Терминология ГОСТ Р 53953 2010: Электросвязь железнодорожная. Термины и определения оригинал документа: 39 (железнодорожная) телеграфная сеть: Сеть железнодорожной электросвязи, представляющая собой совокупность коммутационных станций и узлов,… … Словарь-справочник терминов нормативно-технической документации
Векторная авторегрессия — (VAR, Vector AutoRegression) модель динамики нескольких временных рядов, в которой текущие значения этих рядов зависят от прошлых значений этих же временных рядов. Модель предложена Кристофером Симсом как альтернатива системам одновременных… … Википедия
ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия
Список медицинских сокращений — Эта страница глоссарий. # А … Википедия
Геостационарная орбита — (ГСО) круговая орбита, расположенная над экватором Земли (0° широты), находясь на которой искусственный спутник обращается вокруг планеты с угловой скоростью, равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе… … Википедия
Волгодонск — Город Волгодонск Флаг Герб … Википедия
Белорусы — Белорусы … Википедия
Классификация физических систем
Проведём классификацию физических систем на основе существенных свойств их математических моделей.
Стационарные и нестационарные системы
Система называется стационарной, если её выходная реакция не зависит от того, в какой момент времени поступает сигнал, т. е.
Стационарная система называется также системой с постоянными параметрами. Если же свойства системы не инвариантны относительно начала отсчёта времени, то такую систему называют нестационарной (системой с переменными параметрами, или параметрической системой).
Линейные и нелинейные системы
Система называется линейной, если в ней выполняется принцип суперпозиции, математически записываемый в виде следующих равенств:
Если эти условия не выполняются, то система является нелинейной. Строго говоря, все физические системы, используемые в измерительной технике, в той или иной степени нелинейны. Однако существует много систем, которые весьма точно описываются линейными моделями. Так, практически всегда можно пренебречь нелинейностью обычных резисторов, конденсаторов, некоторых индуктивных элементов, входящих в состав измерительных цепей.
Из принципа суперпозиции и из условия стационарности вытекает важное следствие — гармонический сигнал, проходя через линейную стационарную систему, сохраняет свою форму, приобретая лишь другие амплитуду и начальную фазу.
Сосредоточенные и распределённые системы
Критерием этой классификации является соотношение физических размеров элементов системы l и рабочей длины волны λ генерируемых или транслируемых сигналов. Если характерный размер системы l ≪ λ, то система относится к классу сосредоточенных. Свойства сосредоточенных систем слабо зависят от конфигурации соединительных проводников, поэтому для их описания используют так называемые принципиальные схемы. Так, в радиотехнике сосредоточенные системы широко применяют до рабочих частот в несколько сотен МГц. Лишь при частотах свыше тысячи МГц (СВЧ-диапазон) на смену сосредоточенным системам приходят системы с распределёнными параметрами. Их расчёт составляет содержание отдельных радиотехнических дисциплин.
Стационарная система
69. Стационарная система
Система, в которой сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала
Смотри также родственные термины:
3.18 Стационарная система пенного пожаротушения (неавтоматическая): Включает резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации этих систем должны обеспечить включение резервных насосов в случае, если основные неисправны или не обеспечивают расчетный напор.
Полезное
Смотреть что такое «Стационарная система» в других словарях:
стационарная система — stacionarioji sistema statusas T sritis automatika atitikmenys: angl. time invariant system vok. zeitinvariantes System, n rus. стационарная система, f pranc. système stationnaire, m … Automatikos terminų žodynas
Стационарная система пенного пожаротушения (неавтоматическая) — 3.18 Стационарная система пенного пожаротушения (неавтоматическая): Включает резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации этих систем должны обеспечить включение… … Словарь-справочник терминов нормативно-технической документации
Стационарная система связи — часть системы управления, построенная на базе стационарных узлов и линий связи … Пограничный словарь
Линейная стационарная система — Теория линейных стационарных систем раздел теории динамических систем, изучающая поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и … Википедия
Стационарная гидростатическая система — Прибор для измерения осадок фундаментов, состоящий из большого числа водомерных стаканов пьезометров, жестко укрепленных на фундаментах или конструкциях здания (сооружения) Источник: ГОСТ 24846 81: Грунты. Методы измерения деформаций оснований… … Словарь-справочник терминов нормативно-технической документации
Система небесных координат — используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере.… … Википедия
система пенного тушения пожаров стационарная (неавтоматическая) — Совокупность стационарных технических средств для тушения пожара за счет выпуска пены. Примечание Средства автоматизации этих систем должны обеспечить включение основных и резервных насосов в случае, если основные неисправны или не обеспечивают… … Справочник технического переводчика
Система стационарная пенного пожаротушения (неавтоматическая) — комплект оборудования, включающий резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации систем должны обеспечить включение резервных насосов в случае, если основные… … Словарь-справочник терминов нормативно-технической документации
стационарная система
Смотреть что такое «стационарная система» в других словарях:
Стационарная система — 69. Стационарная система Система, в которой сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала Источник: ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения … Словарь-справочник терминов нормативно-технической документации
стационарная система — stacionarioji sistema statusas T sritis automatika atitikmenys: angl. time invariant system vok. zeitinvariantes System, n rus. стационарная система, f pranc. système stationnaire, m … Automatikos terminų žodynas
Стационарная система пенного пожаротушения (неавтоматическая) — 3.18 Стационарная система пенного пожаротушения (неавтоматическая): Включает резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации этих систем должны обеспечить включение… … Словарь-справочник терминов нормативно-технической документации
Стационарная система связи — часть системы управления, построенная на базе стационарных узлов и линий связи … Пограничный словарь
Линейная стационарная система — Теория линейных стационарных систем раздел теории динамических систем, изучающая поведение и динамические свойства линейных стационарных систем (ЛСС). Широко используется в процессе управления техническими системами, цифровой обработке сигналов и … Википедия
Стационарная гидростатическая система — Прибор для измерения осадок фундаментов, состоящий из большого числа водомерных стаканов пьезометров, жестко укрепленных на фундаментах или конструкциях здания (сооружения) Источник: ГОСТ 24846 81: Грунты. Методы измерения деформаций оснований… … Словарь-справочник терминов нормативно-технической документации
Система небесных координат — используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере.… … Википедия
система пенного тушения пожаров стационарная (неавтоматическая) — Совокупность стационарных технических средств для тушения пожара за счет выпуска пены. Примечание Средства автоматизации этих систем должны обеспечить включение основных и резервных насосов в случае, если основные неисправны или не обеспечивают… … Справочник технического переводчика
Система стационарная пенного пожаротушения (неавтоматическая) — комплект оборудования, включающий резервуары для воды и пенообразователя, насосную станцию и сеть растворопроводов с пожарными гидрантами. Средства автоматизации систем должны обеспечить включение резервных насосов в случае, если основные… … Словарь-справочник терминов нормативно-технической документации
Некоторые характеристики САУ
Системы непрерывного и дискретного действия
Системы стационарные и нестационарные
Стационарной называется система, все параметры которой не изменяются во времени. Нестационарная система — это система с переменными параметрами или даже структурой. При математическом описании нестационарной системы это проявляется в том, что некоторые коэффициенты описывающего ее дифференциального уравнения являются функциями времени. Пример нестационарной системы — система управления ракетой, масса которой изменяется вследствие расхода топлива.
В соответствии с данным определением, в отличие от нестационарной системы, реакции стационарной системы на одно и то же воздействие не зависит от момента времени приложения этого воздействия.
САУ бывают непрерывного или дискретного действия в зависимости от характера действия составляющих систему звеньев.
Система непрерывного действия или, короче, непрерывная система состоит только из звеньев непрерывного действия, т. е. звеньев, выходная величина которых изменяется плавно и непрерывно при плавном изменении входной величины.
Система дискретного действия или дискретная система — это система, содержащая хотя бы одно звено дискретного действия. Звеном дискретного действия называется звено, выходная величина которого изменяется дискретно, т. е. скачками, даже при плавном изменении входной величины. (Скачки выходной величины могут происходить либо при прохождении входной величиной определенных пороговых значений — это звено релейного действия, либо в определенные моменты времени — звено импульсного действия.)
Устойчивость — это свойство системы возвращаться в установившееся состояние после того, как она была выведена из этого состояния каким-либо возмущением. Замкнутые САУ, как всякие замкнутые системы, весьма склонны к потере устойчивости, что чаще всего проявляется в возникновении расходящихся колебаний (генерации). Можно сказать, что устойчивость является необходимым условием работоспособности всякой САУ.
Качество процесса управления характеризуется тем, насколько процесс управления близок к желаемому. Количественно оно определяется показателями (критериями) качества, которые выбираются в соответствии с целью управления.
Важным показателем качества управления является точность управления. Например, для системы регулирования напряжения генератора точность определяется величиной установившегося отклонения напряжения генератора от заданного значения по окончании переходного процесса.
Идентификация объектов управления — это определение их математического описания — математической модели по экспериментальным данным их функционирования и априорным сведениям о таких объектах.
Наблюдаемость — это наличие допустимых измерению выходных координат вектора X, достаточных для определения текущего состояния объекта управления и, следовательно, для управления этим состоянием.
|
Типовые звенья систем автоматического управления
Одномерная линейная непрерывная нестационарная система управления описывается дифференциальным уравнением
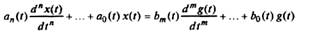 (1) (1) |
с начальными условиями
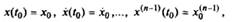 (2) (2) |
где 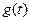
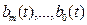
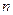

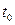
Если коэффициенты уравнения постоянны, система называется линейной стационарной.
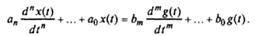 (3) (3) |
В операторной форме уравнение (1) имеет вид
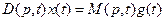
где 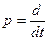

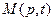
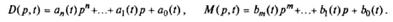 |
Уравнение (3) в операторной форме имеет вид
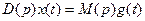
Из операторной формы уравнения следует способ изображения стационарной системы на структурных схемах (рис. 13.1).
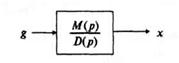 |
Сложные системы управления, как правило, состоят из элементарных и
типовых звеньев.
1. Усилительное звено описывается уравнением
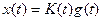
где 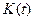

2. Дифференцирующее звено описывается уравнением
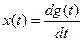
Выходной сигнал равен производной входного сигнала. Уравнение (6) в операторной форме имеет вид
3. Интегрирующее звено описывается уравнением
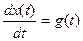
Выходной сигнал получается в результате интегрирования входного. В операторной форме уравнение (6) имеет вид 
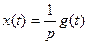
4. Звено чистого запаздывания описывается уравнением 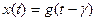
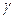
|
Связь структурной схемы с дифференциальным уравнением
1. Построение структурной схемы по дифференциальному уравнению. Структурные схемы строятся с помощью элементарных, типовых звеньев и сумматоров, описывающих преобразование сигналов. Они служат одним из языков описания систем управления. По структурным схемам, как правило, находится эквивалентный оператор системы управления, а затем решаются различные задачи анализа.
АЛГОРИТМ ПОСТРОЕНИЯ СТРУКТУРНОЙ СХЕМЫ
1. Выразить член со старшей производной из дифференциального уравнения (1.3) и представить полученное соотношение с помощью сумматора, дифференцирующих и усилительных звеньев.
2. Все низшие производные получить как сигналы на соответствующих выходах последовательно соединенных интегрирующих звеньев.
3. Начальные условия (2) представить как постоянные во времени воздействия, приложенные на выходах интегрирующих звеньев.
Пример 1.1. Построить структурную схему системы, описываемой дифференциальным уравнением
с начальными условиями 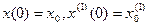
Выразим из уравнения член со старшей производной:
Изобразим схему получения сигнала 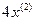
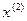
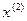
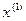
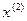
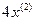
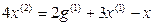
 |
Для этого добавляем к прямой цепи соединение дифференцирующего и усилительного звеньев, которые из входного сигнала 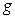

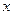
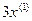
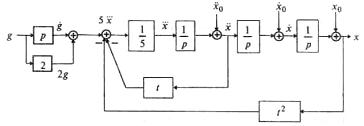
Пример 1.2. Построить структурную схему системы, описываемой дифференциальным уравнением
с начальными условиями 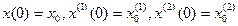
Выразим из уравнения член со старшей производной:
Согласно алгоритму получим структурную схему системы (рис. 13.3).
 |
Пример 1.3. Построить структурную схему системы, описываемой дифференциальным уравнением
Выразим из уравнения член со старшей производной:
и с помощью алгоритма получим схему (рис. 13.4)
 |
2. Составление дифференциального уравнения по структурной схеме.Для записи дифференциального уравнения следует обозначить на схеме все промежуточные сигналы, записать уравнения для каждого звена и для каждого сумматора и из полученной системы дифференциальных и алгебраических уравнений исключить промежуточные переменные кроме входного и выходного сигналов.
Пример 1.4.Составить дифференциальное уравнение по структурной схеме, изображенной на рис. 13.5.
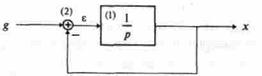 |
Составим уравнения элементов схемы:
1) 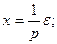
Дифференциальное уравнение системы имеет вид
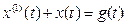
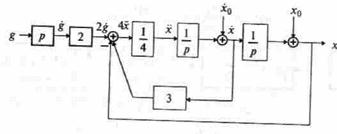
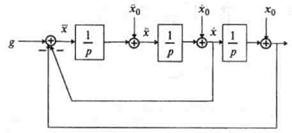
Пример 1.5. Составить дифференциальное уравнение по структурной схеме, представленной на рис. 13.6.
 |
Составим уравнения элементов схемы:
1) 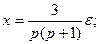
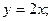
Переходя от операторной формы записи дифференциального уравнения к обычной, получаем
|
Основы управления рисками
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет