Что такое степень 5 класс
Урок 25 Бесплатно Степень числа. Квадрат и куб числа
На данном уроке мы познакомимся с понятием степени числа.
Выясним, что называют «показателем степени» и «основанием степени».
Научимся вычислять квадрат и куб числа.
Составим таблицу степеней первых десяти натуральных чисел и рассмотрим ряд задач с использованием таких таблиц.
Определим, в каком порядке выполняют действия в выражениях, содержащих степень.
Степень числа
Известно, что сумму равных слагаемых можно заменить произведением.
Например, сумму пяти слагаемых, каждое из которых равняется четырем, можно записать короче:
4 + 4 + 4 + 4 + 4 = 5 ∙ 4
В произведении число 5 указывает на количество одинаковых слагаемых.
В свою очередь произведение одинаковых множителей тоже можно записать компактнее.
Произведение n одинаковых множителей можно представить в виде степени.
В буквенном виде произведение равных множителей можно представить следующим образом:
а— любое натуральное число.
Читают «а в n-ной степени» или «а в степени n».
Число а называют основанием (число, возводимое в степень).
n— это показатель степени (число, которое указывает сколько раз повторяется основание степени).
Степень числа представляют всегда так: записывают основание степени, а показатель ее записывают меньше размером в верхнем правом углу основания степени.
Операция умножения одинаковых множителей называется возведением в степень.
Например, произведение пяти множителей, каждое из которых равняется четырем, можно записать так:
4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4 5
Читают данную запись следующим образом:
4 5 — четыре в пятой степени.
Данная степень равна произведению трех двоек.
2— основание степени.
3— показатель степени.
Данная степень равна произведению четырех пятерок.
5— основание степени.
4— показатель степени.
Пройти тест и получить оценку можно после входа или регистрации
Квадрат и куб числа
Вторую степень числа называют квадратом числа.
Так, квадрат любого натурального числа а будет представлять собой произведение двух одинаковых множителей: а ∙ а = а 2 (говорят и читают «а в квадрате»).
2 2 (два во второй степени) иначе говорят и читают «два в квадрате».
10 2 (десять во второй степени) иначе говорят и читают «десять в квадрате».
27 2 (двадцать семь во второй степени) иначе говорят и читают «двадцать семь в квадрате».
Давайте сосчитаем квадраты первого десятка натуральных чисел (возведем во вторую степень первые десять натуральных чисел), используя таблицу умножения.
Один в квадрате равняется одному: 1 2 = 1 ∙ 1 = 1.
Два в квадрате равняется четырем: 2 2 = 2 ∙ 2 = 4.
Три в квадрате равняется девяти: 3 2 = 3 ∙ 3 = 9.
Четыре в квадрате равняется шестнадцати: 4 2 = 4 ∙ 4 = 16.
Пять в квадрате равняется двадцати пяти: 5 2 = 5 ∙ 5 = 25.
Шесть в квадрате равняется тридцати шести: 6 2 = 6 ∙ 6 = 36.
Семь в квадрате равняется сорока девяти: 7 2 = 7 ∙ 7 = 49.
Восемь в квадрате равняется шестидесяти четырем: 8 2 = 8 ∙ 8 = 64.
Девять в квадрате равняется восьмидесяти одному: 9 2 = 9 ∙ 9 = 81.
Десять в квадрате равняется сотне: 10 2 = 10 ∙ 10 = 100.
Оформим полученные данные квадратов натуральных чисел от 1 до 10 в виде таблицы.
Таблица квадратов первых десяти натуральных чисел
Учитывая данные таблицы квадратов, решим уравнение.
Решим уравнение х 2 = 49.
Решить уравнение- это значит найти корень уравнения (в нашем случае установить значение х).
Следовательно, корень уравнения (х) равен семи.
х 2 = 49
х = 7
Проверка: подставим найденное значение неизвестной (х = 7) в исходное уравнение х 2 = 49, получим:
7 2 = 49
7 ∙ 7 = 49
49 = 49
Ответ: х = 7.
У меня есть дополнительная информация к этой части урока!
Чтобы возвести в любую степень число 10, необходимо дописать после единицы нули, количество которых показывает показатель степени.
Разберем пример первый.
Найдите четвертую степень десяти (десять в четвертой степени 10 4 ).
10— это основание.
4— это показатель степени.
Так как по вышеизложенному правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:
10 4 = 1 0000
На самом деле, если перемножить (по определению степени) четыре десятки, то получим:
10 4 = 1 0 ∙ 1 0 ∙ 1 0 ∙ 1 0 = 1 0000
Пример второй: найдите третью степень десяти (десять в третьей степени 10 3 ).
10— это основание.
3— это показатель степени.
Так как по правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:
10 3 = 1 000
Соответственно, если перемножить (по определению степени) три десятки, то получим:
10 3 = 1 0 ∙ 1 0 ∙ 1 0 = 1 000
Рассмотрим обратную ситуацию:
Представим число 100 в виде степени с основанием 10.
Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (1 00 ).
Число 100 содержит два нуля, следовательно, это число в виде степени с основанием 10 представим следующим образом:
1 00 = 10 2
10— это основание.
2— это показатель степени.
Рассмотрим еще один подобный пример.
Представим число 10000 в виде степени с основанием 10.
Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (1 0000 ).
Данное число содержит четыре нуля, следовательно, 10000 в виде степени с основанием 10 представим следующим образом:
1 0000 = 10 4
10— это основание.
4— это показатель степени
Третья степень числа тоже имеет свое название.
Число в третьей степени называют кубом числа.
Так, куб любого натурального числа а будет представлять собой произведение трех одинаковых множителей: а ∙ а ∙ а = а 3 (говорят и читают «а в кубе»).
2 3 (два в третьей степени) иначе говорят и читают «два в кубе».
10 3 (десять в третьей степени) иначе говорят и читают «десять в кубе».
27 3 (двадцать семь в третьей степени) иначе говорят и читают «двадцать семь в кубе».
Давайте определим кубы первого десятка натуральных чисел (возведем в третью степень первые десять натуральных чисел), используя таблицу умножения.
Один в кубе: 1 3 = 1 ∙ 1 ∙ 1 = 1.
Два в кубе: 2 3 = 2 ∙ 2 ∙ 2 = 8.
Три в кубе: 3 3 = 3 ∙ 3 ∙ 3 = 27.
Четыре в кубе: 4 3 = 4 ∙ 4 ∙ 4 = 64.
Пять в кубе: 5 3 = 5 ∙ 5 ∙ 5 = 125.
Шесть в кубе: 6 3 = 6 ∙ 6 ∙ 6 = 216.
Семь в кубе: 7 3 = 7 ∙ 7 ∙ 7 = 343.
Восемь в кубе: 8 3 = 8 ∙ 8 ∙ 8 = 512.
Девять в кубе: 9 3 = 9 ∙ 9 ∙ 9 = 729.
Десять в кубе: 10 3 = 10 ∙ 10 ∙ 10 = 1000.
Оформим полученные данные кубов натуральных чисел от 1 до 10 в виде таблицы.
Таблица кубов первых десяти натуральных чисел
1000
С помощью таблицы кубов можно легко и просто решать примеры и задачи, в которых необходимо высчитывать третью степень числа.
Представим в виде куба число 343.
По таблице кубов видим, что 343 = 7 3
Проверим: найдем произведение трех семерок:
7 3 = 7 ∙ 7 ∙ 7 = 49 ∙ 7 = 343
На прошлом уроке мы подробно разобрали порядок выполнения арифметических действий в выражениях.
Выяснили, что в первую очередь выполняются арифметические действия в скобках, затем-действия второй ступени (умножение и деление) по порядку их следования слева направо, и только потом выполняются действия первой ступени (сложение и вычитание) по порядку слева направо.
Однако, в математических выражениях, в которых отсутствуют скобки, но есть действия первой, второй ступени и степень, возведение в степень выполняется раньше других действий, только потом умножают, делят, складывают и вычитают в установленном правилами порядке.
Если в скобках содержится степенное выражение, то действия в скобках выполняются по порядку слева направо, начиная с действий высшей ступени- возведение в степень, и далее по известным нам правилам.
За скобками действия выполняют, соблюдая порядок выполнения действий без скобок, рассмотренный выше.
Рассмотрим поясняющие примеры.
При решении различных задач и примеров будем пользоваться составленными таблицами степеней.
Пример 1.
Определим порядок действий в выражении и найдем его значение.
Так как исходное выражение не содержит скобки, а возведение в степень- это действие более высокой ступени, чем умножение, деление, сложение и вычитание, следовательно, в первую очередь необходимо выполнить вычисление степени, затем слева направо в порядке следования сначала действия второй ступени (деление), затем- действия первой ступени (вычитание).
1) 8 2 = 8 ∙ 8 = 64 (по определению степени или по таблице квадратов).
2) 64 ÷ 4 = 16
Пример 2.
Найдем значение данного выражения, определив порядок действий в нем.
Согласно порядка выполнения действий сначала выполняются действия в скобках.
Найдем разность 21 и 11.
Далее выполняется действие высшей ступени (возведение в степень), т.е. разность, полученную в скобках, возведем в квадрат.
Найдем, чему равно 10 2 по определению степени или по таблице квадратов.
2) 10 2 = 10 ∙ 10 = 100
Затем выполним действия, которые находятся в исходном выражении за скобками.
Определим третью степень двойки по таблице кубов или по определению степеней.
3) 2 3 = 2 ∙ 2 ∙ 2 = 8
4) 100 ∙ 8 = 800
У меня есть дополнительная информация к этой части урока!
С давних пор основными арифметическими операциями являются операции сложения, вычитания, умножения и деления.
Представление о степени, как об отдельной операции возникло не сразу.
Однако степени применялись при вычислении площадей и объемов уже у древних народов: степень числа высчитывали при решении различных задач в Древнем Египте, Древней Греции, в Вавилоне.
Диофант Александрийский древнегреческий математик, философ (III век н.э.) в своем знаменитом труде «Арифметика» описал первые натуральные степени чисел.
Диофант первым из античных ученых предложил специальные обозначения для шести степеней неизвестного (квадрат, куб, квадрато-квадраты, квадрато-кубы и т.д.)
Древнегреческий ученый Пифагор и его последователи (пифагорейцы) проявляли большой интерес к числам, искали в них скрытый смысл, закономерности и приписывали им различные свойства.
Пифагорейцы предполагали, что каждое число можно представить в виде фигуры.
Так, например, числа 4, 9, 16, 25 они представляли в виде квадратов.
В Древнем Вавилоне для вычисления и расчетов был создан целый ряд вычислительных таблиц: таблицы умножения, таблицы квадратов и кубов и многие другие.
В Древней Индии успешно развивалась наука.
Высоких результатов индийцы добились в астрономии, медицине, математике.
Индийские ученые часто оперировали большими числами.
В Древней Индии существовало понятие степени числа, математики того времени умели вычислять площади и объемы фигур, разработали алгоритмы вычисления всех арифметических операций, в том числе определение степени числа.
Важнейшим открытием индийских ученых в математике стало изобретение позиционной системы счисления, а также запись (чтение) чисел, для каждой цифры был придуман свой знак.
Математические труды их были изложены в основном в словесной форме на древнеиндийском языке в священных писаниях, книгах, сказаниях.
Потребность в решении более сложных математических задач со степенями заставляла ученых разных стран расширять понятие о степени, систематизировать и обобщать известные уже данные о ней.
В начале XV века самаркандский математик Гияс ад-Дин Джемшид Аль-Каши рассматривал нулевой показатель степени, в это же время французский ученый Никола Шюке применял в своих трудах нулевой и отрицательный показатель степени.
В 1544 г. немецкий математик Михаэль Штифель в своей книге «Полная арифметика» впервые ввел понятие «Показатель степени».
Постепенно понятие степени становится все шире, оно применяется не только к числу, но и к переменной.
Математики средневековья пытались установить единое обозначение степени и сделать ее компактней.
Французский ученый математик Франсуа Виет ввел буквенное обозначение (N, Q, C) для первой, второй и третьей степени.
Нидерландский математик Симон Стевин предложил называть степень по их показателям, отвергая тем самым словесные обозначения степеней, составленные Диофантом.
Современное обозначение степеней (а n ), где а-основание степени, n-показатель степени, ввел французский математик Рене Декарт.
Пройти тест и получить оценку можно после входа или регистрации
Математика. 5 класс
Конспект урока
Степень с натуральным показателем
Перечень вопросов, рассматриваемых в теме:
— понятие степени с натуральным показателем;
— вычисление квадрата числа;
— вычисление куба числа.
Квадрат числа – это вторая степень числа.
Куб числа – это третья степень числа.
Теоретический материал для самостоятельного изучения
Нам известно, что сумму нескольких одинаковых слагаемых принято записывать короче – в виде произведения:
4 + 4 + 4 + 4 + 4 = 4 ∙ 5
Произведение одинаковых чисел также можно записать короче:
4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4 5
Это произведение можно записать короче, полученный результат называют степенью. Читается так: «четыре в пятой степени».
Запись 4 3 (четыре в степени три) означает 4 ∙ 4 ∙ 4. При этом число 4 называют основанием степени, а число 3 – показателем степени. Число три показывает, сколько раз нужно взять множителем основание степени – число 4: 4 3 = 4 ∙ 4 ∙ 4 = 64.
Степенью числа а с натуральным показателем n (n > 1) называют произведение n натуральных множителей, каждый из которых равен а:
Таким образом, можно вычислить любую степень числа с натуральным показателем, большим единицы. Стоит запомнить, что любое число в первой степени будет ровняться ему самому, т. е. a 1 = a.
Вторую степень числа называют квадратом числа. Запись 4 2 читают «четыре в квадрате». Третью степень числа называют кубом числа. Запись 4 3 читают «четыре в кубе».
Обратите внимание на таблицы квадратов и кубов натуральных чисел. Со временем вы их запомните.
Разбор решения заданий тренировочного модуля
№ 1. Найдите чему равно 13 4 = ____.
№ 2. Чему равна пятая степень 19? Выберите верный ответ.
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 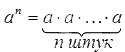
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).
Степень числа

Всего получено оценок: 164.
Всего получено оценок: 164.
Степень – это еще один тема в изучении арифметических действий. Первой было сложение и вычитание, второй – умножение и деление, третьей станет возведение в степень и извлечение корня. Знание степеней и их свойств позволяет значительно ускорить счет, а зачастую без этих знаний не обойтись при решении уравнений математики 5 класса.
Определение
Что значит возвести в степень? Это значит умножить число само на себя какое-то количество раз. Какое именно – показывает показатель степени. Сама степень состоит из двух частей. Основание – это то число, которое мы будем умножать само на себя. Показатель – это число, показывающее сколько раз число нужно умножить само на себя. Вот и вся формула степени числа.
Понимание разных частей формулы степени обязательно. Поскольку без него будет трудно в дальнейшем понять, что же такое логарифм.
Чаще всего возводится в квадрат, потому что числа в квадрате очень часто применяются в физических и математических вычислениях. Но и более высокие степени есть и нужно уметь их вычислять. Специально для квадратов и кубов составлены краткие таблицы, которые позволяют быстро вычислить то или иное значение степени, без вычислений по возведению.
Свойство степеней
У степени всего 6 свойств. Для каждого из них есть буквенная формулировка.
Свойства это хороший вариант быстро подсчитать результат больших чисел. Найти число в степени не так трудно, особенно с современными калькуляторами и таблицами степеней. А вот понять, какое именно число и в какую степень возводить, это уже задача для человеческого ума.
Корень
Обратное действие для возведения в степень это извлечение корня. Извлечение корня подразумевает под собой необходимость узнать, какое число возводили в ту или иную степень, чтобы получилось искомое число.
Если мы ищем квадратный корень из 4, то необходимо узнать, какое натуральное число возводилось в квадрат для получения числа 4.
Что мы узнали?
Мы дали определение степени числа, разобрали, как расписывается степень в выражениях. Определили 6 свойств степени, привели формулировку и буквенную запись для каждой из них. Поговорили об обратном для степени действии – корне, о его значении и способах вычисления.












