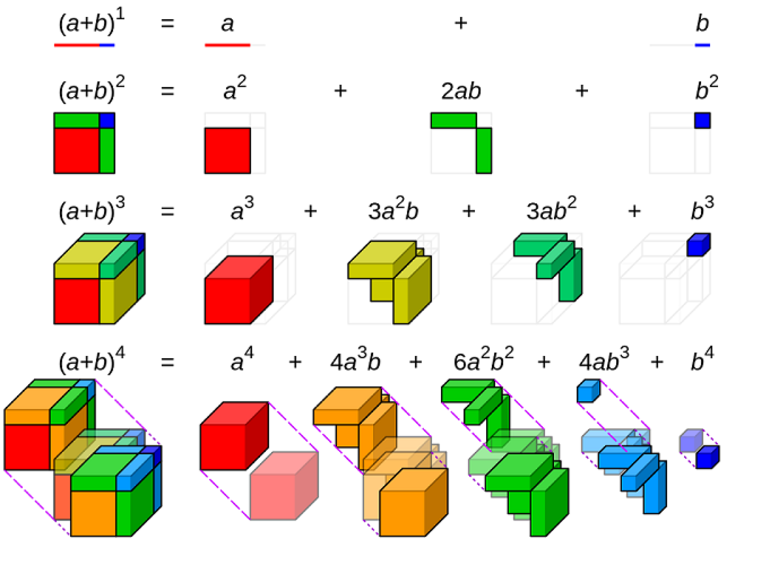
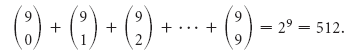Что такое степень бинома

Бином Ньютона

Из Википедии — свободной энциклопедии

Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

( a + b ) n = ∑ k = 0 n ( n k ) a n − k b k = ( n 0 ) a n + ( n 1 ) a n − 1 b + ⋯ + ( n k ) a n − k b k + ⋯ + ( n n ) b n <\displaystyle (a+b)^=\sum _^<\binom >a^b^=a^+a^b+\dots +a^b^+\dots +b^>

В таком виде эта формула была известна ещё индийским и персидским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное действительное число (позднее она была распространена и на комплексные числа). В общем случае бином представляет собой бесконечный ряд (см. ниже).

( x + y ) 2 = x 2 + 2 x y + y 2 ( x + y ) 3 = x 3 + 3 x 2 y + 3 x y 2 + y 3 ( x + y ) 4 = x 4 + 4 x 3 y + 6 x 2 y 2 + 4 x y 3 + y 4 ( x + y ) 5 = x 5 + 5 x 4 y + 10 x 3 y 2 + 10 x 2 y 3 + 5 x y 4 + y 5 <\displaystyle <\begin(x+y)^<2>&=x^<2>+2xy+y^<2>\\[8pt](x+y)^<3>&=x^<3>+3x^<2>y+3xy^<2>+y^<3>\\[8pt](x+y)^<4>&=x^<4>+4x^<3>y+6x^<2>y^<2>+4xy^<3>+y^<4>\\[8pt](x+y)^<5>&=x^<5>+5x^<4>y+10x^<3>y^<2>+10x^<2>y^<3>+5xy^<4>+y^<5>\\[8pt]\end>>

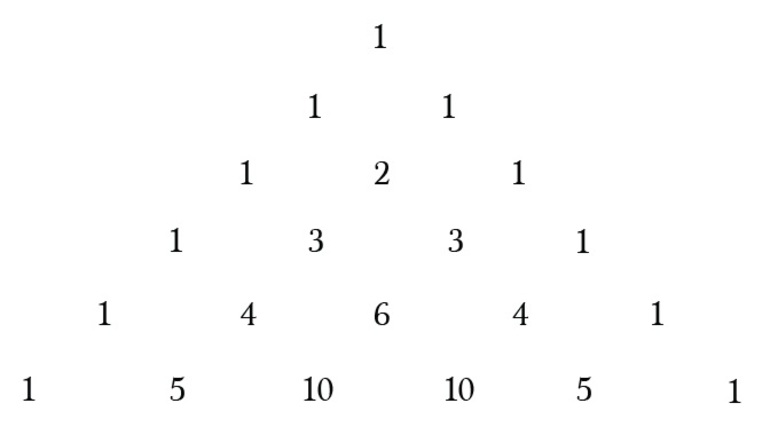
Для быстрого разложения бывает удобно воспользоваться треугольником Паскаля.

Источник

Древние знания

Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.

Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.

Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.

Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.

Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:

К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.

Утверждение теоремы

Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.

Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :

Теорема может быть применена к степеням любого бинома.

С точки зрения геометрии

Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.

Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:

Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.

Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.

Биномные обобщения

Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.

Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.

Короткий путь

Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.

Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).

Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.

Источник

Бином Ньютона

Биноминальное разложение с использованием треугольника Паскаля

1. В каждом выражении на одно слагаемое больше, чем показатель степени n.

2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.

3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.

4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до «половины пути», а потом уменьшаются на те же значения обратно к 1.

первой и последнее числа 1;
второе число равно 1 + 5, или 6;
третье число это 5 + 10, или 15;
четвертое число это 10 + 10, или 20;
пятое число это 10 + 5, или 15; и
шестое число это 5 + 1, или 6.

Мы можем обобщить наши результаты следующим образом.

Бином Ньютона с использованием треугольника Паскаля

Разложение бинома используя значения факториала

Бином Ньютона с использованием обозначение факториала

Для любого бинома (a + b) и любого натурального числа n,
.

Бином Ньютона может быть доказан методом математической индукции. Она показывает почему 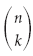называется биноминальным коэффициентом.

Нахождение определенного члена

Предположим, что мы хотим определить тот или иной член термин из выражения. Метод, который мы разработали, позволит нам найти этот член без вычисления всех строк треугольника Паскаля или всех предыдущих коэффициентов.

Обратите внимание, что в биноме Ньютона дает нам 1-й член, дает нам 2-й член, дает нам 3-й член и так далее. Это может быть обощено следующим образом.

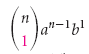
Нахождение (k + 1) члена

(k + 1) член выражения (a + b) n есть .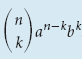

Общее число подмножеств

Полное число подмножеств

Пример 7 Сколько подмножеств имеет множество ?

Решение Начинки на каждый гамбургер являются элементами подмножества множества всех возможных начинок, а пустое множество это просто гамбургер. Общее число возможных гамбургеров будет равно

. Таким образом, Венди может предложить 512 различных гамбургеров.

Источник

Бином Ньютона — формула, доказательство и примеры решения

Древние знания

Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.

Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.

К VI веку н. э. индийские математики, вероятно, знали способ выразить общее правило, как частное, и выражали это примерно в таком виде: n! / (n — k)!k!. Чёткое его изложение можно найти в тексте XII века, автор которого — Бхаскар. Насколько известно, первая формулировка биноминальной теоремы и соответствующая таблица коэффициентов найдена в работе Аль-Караджи, которая цитируется Аль-Самавалем в его трудах.

Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.

Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.

В 1544 году Майкл Стифель ввёл термин «биномиальный коэффициент» и показал, как его использовать для выражения (1 + a) n с точки зрения (1 + a) n — 1 через «треугольник Паскаля». Блез Паскаль всесторонне изучил треугольник в трактате «Traité du triangle arithmétique» (1653).

Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:

К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.

Утверждение теоремы

Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.

Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :

Теорема может быть применена к степеням любого бинома.

С точки зрения геометрии

Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.

Биномиальные коэффициенты появляются в разложении бинома Ньютона. Обычно их записывают как ( n k) и интерпретируют, как количество способов выбора k элементов из n строки треугольника Паскаля. Коэффициент x n — k y k находят по формуле: ( n k) = n! / k! (n-k)!, которая определяется в терминах факториальной функции n!.

Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:

Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.

Или, например, общий случай. Расширение (x + y) n дает сумму 2 n произведений вида e1 e2 … en, где каждый ei равен x или y. Коэффициенты перестановки показывают, что каждый продукт равен x n — k y k для некоторого k между 0 и n. Для заданного k следующие значения равны по порядку:

Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.

Биномные обобщения

Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.

Однако для произвольного числа r можно вычислить ( r k) = r(r — 1) ··· (r — k + 1) / k! = (r)k / k!, где (·) k является символом Похгаммера, который здесь означает падающий факториал. Это согласуется с обычными определениями. Когда r — неотрицательное целое число, биномиальные коэффициенты при k > r равны нулю, поэтому это уравнение сводится к обычной биномиальной теореме, где существует не более r + 1 ненулевых членов. Для других значений r ряд обычно имеет бесконечно много ненулевых членов.

Обобщения можно распространить на случай, когда x и y — комплексные числа. Для этой версии следует снова принять | х | > | у | и определить степени x + y и x, используя голоморфную ветвь логарифма, определённую на открытом диске радиуса | х | с центром в х. Обобщённая теорема бинома справедлива и для элементов х и у в банаховой алгебре, пока х = ух, х является обратимым, а || у / х || Проверка в действии

Начать лучше с решения простой задачи, которую учитель покажет классу на уроке алгебры. Например, нужно расширить (2x-3) ³. Это было бы не слишком трудно сделать, воспользовавшись онлайн-калькулятором. Но нужно использовать бином, когда придётся столкнуться с более крупными расширениями, такими как двучлены, возведённые в 4, 5, 6, … степени.

Для начала нужно определить два члена из бинома (положения x и y формулы) и степени (буква n), до которой нужно расширить бином. Например, чтобы расширить (2x-3) ³, два члена составляют 2x и -3, а значение мощности (или n) равно 3. Следует отметить, что всякий раз, когда в биноме есть знак вычитания, очень важно помнить, что минус следует использовать только в качестве отрицательного символа в сопутствующем термине.

Замечательная вещь в теореме о биноме — это то, что она позволяет найти расширенный многочлен без умножения множества биномов вместе. Довольно интересное свойство. Оказывается, что число слагаемых в искомом расширенном полиноме всегда будет на единицу больше, чем сила, которую расширяют. Это означает, что необходимо создавать многочлен с четырьмя членами, так как мощность в этом примере равна 3.

Каждый член будет иметь (2x) и (-3), а также формулу «n выбирает k», где n = 3. Нужно записать это 4 раза, по одному на каждый член, оставив значение k в «n выбирает k». На этом этапе подсчёта значения степеней не заполняются.

Далее нужно заполнить k-значения и полномочия. Здесь можно следовать формуле суммирования, увеличивая мощность для каждого члена. Но довольно просто следовать шаблонам. Значения k в «n выбирает k» начинаются с k = 0 и увеличиваются на 1 в каждом члене. Последний член должен заканчиваться на n, равный k, в этом случае n = 3 и k = 3. Затем нужно добавить полномочия на (2x) и (-3).

Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.

Короткий путь

Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.

Теперь хорошая часть. В Треугольнике Паскаля спрятаны все ответы — это настоящая шпаргалка. Диаграмма ниже показывает, где находятся скрытые «n выбирает k».

Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).

Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.

Источник

Бином Ньютона.

Навигация по странице.

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.

Треугольник Паскаля.

Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:

Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n :

Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Свойства биномиальных коэффициентов.

Первые два свойства являются свойствами числа сочетаний.

Доказательство формулы бинома Ньютона.

Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства .

Получили верное равенство.

Докажем, что верно равенство , основываясь на предположении второго пункта.

Поехали!

Раскрываем скобки

Группируем слагаемые

Так как и , то ; так как и , то ; более того, используя свойство сочетаний , получим

Подставив эти результаты в полученное выше равенство

придем к формуле бинома Ньютона .

Этим доказана формула бинома Ньютона.

Рассмотрим подробные решения примеров, в которых применяется формула бинома Ньютона.

Напишите разложение выражения (a+b) 5 по формуле бинома Ньютона.

Найдите коэффициент бинома Ньютона для шестого члена разложения выражения .

В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Доказать, что значение выражения , где n – натуральное число, делится на 16 без остатка.

Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:

Источник