Что такое степень числа с рациональным показателем
Степень с рациональным показателем
Мы уже знакомы с понятием степени с целым показателем. Давайте разберемся, что такое степень с рациональным показателем.
Рациональный показатель – это выражение вида \(\frac
\), где \(p\)-некоторое целое число, а \(q\) – натуральное число, причем \(q\ge2\).
Положительное число \(a\) в рациональной степени \(\frac
\) является арифметическим корнем степени \(q\) из числа \(a\) в степени \(p\):
Обращаем ваше внимание, что
Неважно в каком порядке – сначала извлечь корень или возвести в степень, от этого смысл выражения не теряется. Как удобнее, так и считайте.
Пусть есть некоторое положительное число \(a\) и целое число \(p\), тогда справедливы следующие соотношения:
где \(k\) и \(q\) – натуральные числа большие 1.
Давайте попробуем их доказать:
Из определения степени с рациональным показателем следует, что:
Опять из определения и свойства корня n-й степени следует:
Третья формула на наш взгляд очевидна, просто сократить степень справа и получите исходное выражение.
Свойства степени с рациональным показателем
Пусть \(a\) и \(b\) – некоторые положительные числа, а числа \(m\) и \(n\) – рациональные числа. Тогда выполняются соотношения:
При умножении степеней с рациональным показателем и одинаковым основанием их показатели степени складываются.
При делении степеней с рациональным показателем и одинаковым основанием их показатели степени вычитаются.
При возведении степени с рациональным показателем в степень с рациональным показателем их показатели перемножаются.
Степень с рациональным показателем от произведения двух положительных чисел равна произведению степеней этих множителей.
Степень с рациональным показателем от частного двух положительных чисел равна частному степеней этих чисел.
И еще два очень важных свойства степеней. Они вам понадобятся при решении показательных уравнений и неравенств.
Пусть опять есть некоторое положительное число \(a>1\) и рациональные числа \(n\) и \(m\).
При \(n \gt 0\) \(a^n \gt 1\),
При \(n \lt 0\) \(0 \lt a^n \lt 1\).
Если же \(a \gt 1\) и \(n \gt m\), то
Если \( 0 \lt a \lt 1 \) и \(n \gt m\), то
Разберем несколько примеров:
Так как основание степени больше единицы \(3 \gt 1\) и \(\frac<1> <3>\lt \frac<1><2>\).
Так как \(0 \lt \frac<1> <5>\lt 1\) и \(\frac<1> <3>\lt \frac<1><2>\)
Описание урока
От успешной сдачи государственного экзамена по математике зависит поступление в высшее учебное заведение. Степень с рациональным показателем – важная тема, изучение которой необходимо для успешной подготовки к ЕГЭ. От того, насколько хорошо она освоена, зависит в будущем, насколько легко будет решать уравнения и производить более сложные операции с числами. Задание номер 15 строится на умении работать с такими степенями. Чтобы понимать, о чём идёт речь, стоит ознакомиться с определением степени с рациональным показателем и её основными свойствами, которые пригодятся и при работе с функциями.
Важно запомнить, что число А не должно быть меньше 0, а число q не равно 1.
Свойства степени с рациональным показателем
Знание свойств степеней с показателем, равным рациональному числу, облегчает работу с уравнениями и функциями, где содержатся такие выражения. Внимательно их изучив, можно достаточно быстро выполнять задания, что немаловажно в процессе написания ЕГЭ.
Одно из основных свойств: произведение двух степеней с одинаковым основанием равно основанию в степени, равной сумме степеней двух множителей.
При делении степеней с рациональным показателем из показателя делимого вычитают показатель делителя. У степени с рациональным показателем есть и другие свойства, которые также присущи степени с обыкновенным показателем. Их легко запомнить, а чтобы примеры помогли внимательнее рассмотреть свойства, посмотрите видео, в котором о них рассказывается подробнее.
1.1.6 Степень с рациональным показателем и её свойства
Видеоурок 1: Степень с рациональным показателем
Видеоурок 2: Степень с рациональным показателем. Решение примеров
Лекция: Степень с рациональным показателем и её свойства

Любую степень с рациональным показателем можно представить в виде корня, чья степень будет равна знаменателю дроби, находящейся в показателе степени, а числитель будет степенью подкоренного выражения.

Все, перечисленные ниже степени используются для рациональных чисел p, q и для положительных a, b.
1. Если Вам необходимо умножить две степени с рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.
2. Если необходимо разделить две степени c рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть.
3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.
4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.
5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.
6. Если некоторая дробь имеет отрицательный рациональный показатель степени, то для избавления от знака минуса, её следует перевернуть.
Очень важно помнить, что знак степени не влияет на знак выражения при возведении в степень.
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 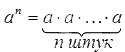
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).




