Что такое степень числа в математике определение

Что такое степень числа

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

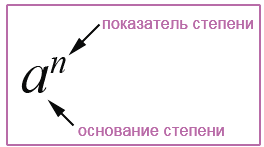
Выражение 4 6 называют степенью числа, где:

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Исключение составляют записи:

Конечно, выражения выше можно читать и по определению степени:

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Квадрат любого числа есть положительное число или нуль, то есть:

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

Пример. Вычислить: −6 2 − (−1) 4

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Источник

Степень числа. Квадрат и куб числа

Определение.

Степенью числа «» с натуральным показателем ««, большим 1, называется произведение «» одинаковых множителей, каждый из которых равен числу ««.

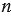
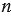
Например, найдем значение следующих степеней:

2 4 = 2222 = 422 = 82 = 16;

3 6 = 333333 = 93333 = 27333 = 8133 =2433 = 729.

Например, найдем квадрат чисел 4 и 8:

4 2 = 44 = 16;

8 2 = 88 = 64.

Например, найдем куб чисел 5 и 7:

5 3 = 555 = 255 = 125;

7 3 = 777 = 495 = 343;

Степенью числа «» с показателем = 1 является само это число, то есть .

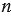
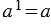
Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:

Поделись с друзьями в социальных сетях:

Источник

Возведение в степень: правила, примеры

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Решение

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Решение

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Как возвести число в целую степень

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Решение

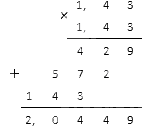
Решение

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

Как возвести число в дробную степень

Проиллюстрируем на примере.

Решение

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Решение

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Вычислите приближенное значение 2 в степени 1,174367.

Решение

Источник

Степень и ее свойства. Определение степени

Разделы: Математика

Ознакомить учащихся со свойствами степеней с натуральными показателями и научить выполнять действия со степенями.

Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.

По определению степени:

а n =

Нахождение значения степени называют возведением в степень.

1. Примеры возведения в степень:

2. Представьте в виде квадрата числа: 25 ; 0,09 ;

25 = 5 2 ; 0,09 = ( 0,3 ) 2 ; .

3. Представьте в виде куба числа:

4. Найти значения выражений:

а) 3• 10 3 = 3• 10• 10• 10 = 3• 1000 = 3000

1. Запишите произведение в виде степени:

б)

2. Представьте в виде квадрата числа:

16 ; 0,25 ; .

3. Представьте в виде куба числа:

125 ; 0,027 ; .

4. Найти значения выражений :

Для любого числа а и произвольных чисел m и n выполняется:

Правило: При умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.

a m a n a k = a m + n a k = a ( m + n ) + k = a m + n + k

1. Представить в виде степени:

б) y• y 6 = y 1 • y 6 = y 1 + 6 = y 7

в) b 2 • b 5 • b 4 = b 2 + 5 + 4 = b 11

г) 3 4 • 9 = 3 4 • 3 2 = 3 6

д) 0,01• 0,1 3 = 0,1 2 • 0,1 3 = 0,1 5

2. Представить в виде степени и найти значение по таблице:

б) 3 2 • 3 5 = 3 7 = 2187

1. Представить в виде степени:

д) 2 3 •2 4 к) 0,3 3 •0,09

2. Представить в виде степени и найти значение по таблице:

б) 3 4 •3 2 г) 27• 243

Для любого числа а0 и произвольных натуральных чисел m и n, таких, что m>n выполняется:

по определению частного:

Правило: При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Определение: Степень числа а, не равного нулю, с нулевым показателем равна единице:

1. Представьте в виде степени частное:

г) с 5 :с 0 = с 5 :1 = с 5

2. Найдите значения выражений:

б) 10 20 :10 17 = 10 3 = 1000

в)

г)

д)

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

Возведение в степень произведения.

Для любых а и b и произвольного натурального числа n:

По определению степени

( ab ) n =

Сгруппировав отдельно множители а и множители b, получим:

=

Доказанное свойство степени произведения распространяется на степень произведения трех и более множителей.

( a• b• c ) n = a n •b n •c n ;

Правило: При возведении в степень произведения возводят в эту степень каждый множитель и результат перемножают.

1. Возвести в степень:

б) (2• х• у ) 3 =2 3 •х 3 •у 3 = 8• х 3 •у 3

в) ( 3• а ) 4 = 3 4 •а 4 = 81• а 4

д) (-0,2• х• у ) 2 = (-0,2) 2 •х 2 •у 2 = 0,04• х 2 •у 2

е) (-3• a• b• c ) 4 = (-3) 4 •a 4 •b 4 •c 4 = 81• a 4 •b 4 •c 4

2. Найти значение выражения:

а) (2• 10) 4 = 2 4 •10 4 = 16• 1000 = 16000

б) (3• 5• 20) 2 = 3 2 •100 2 = 9• 10000= 90000

в) 2 4 •5 4 = (2• 5) 4 = 10 4 = 10000

г) 0,25 11 •4 11 = (0,25• 4) 11 = 1 11 = 1

д)

1. Возвести в степень:

е)

2. Найти значение выражения:

г)

д)

Возведение в степень степени.

Для любого числа а и произвольных натуральных чисел m и n:

По определению степени

( а m ) n =

Правило: При возведении степени в степень основание оставляют тем же, а показатели перемножают.

1. Возвести в степень:

( а 3 ) 2 = а 6 ( х 5 ) 4 = х 20

( у 5 ) 2 = у 10 ( b 3 ) 3 = b 9

2. Упростите выражения:

а) а 3 •( а 2 ) 5 = а 3 •а 10 = а 13

б) ( b 3 ) 2 •b 7 = b 6 •b 7 = b 13

в) ( х 3 ) 2 •( х 2 ) 4 = х 6 •х 8 = х 14

г) ( у• у 7 ) 3 = ( у 8 ) 3 = у 24

3. Найдите значение выражений:

а)

б)

1. Возвести в степень:

в) ( у 3 ) 2 г) ( b 4 ) 4

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

Приложение

1ю Запишите произведение в виде степени:

б)

2. Представьте в виде квадрата числа:

25 ; 0,16 ; .

3. Представьте в виде куба числа:

64 ; 0,125 ; .

4. Найти значения выражений:

1. Запишите произведение в виде степени:

б)

в) с• с• с• с• с• с• с• с• с

2. Представьте в виде квадрата числа: 100 ; 0,49 ; .

3. Представьте в виде куба числа:

1000 ; 0,008 ; .

4. Найти значения выражений :

1. Запишите произведение в виде степени:

б)

д) ( bс ) • ( bс ) • ( bс ) • ( bc )

2. Представьте в виде квадрата числа:

81 ; 0,64 ;.

3. Представьте в виде куба числа:

216 ; 0,064 ; .

4. Найти значения выражений :

1. Представить в виде степени:

д) 2 2 •2 5 к) 0,2 3• 0,04

2. Представить в виде степени и найти значение по таблице:

1. Представить в виде степени:

д) 2 3 •2 6 к) 0,3 4 •0,27

2. Представить в виде степени и найти значение по таблице:

1. Представить в виде степени:

б) х 7 •х 8 ж) 3 4 •27

д) 2 4 •2 5 к) 0,2 2 •0,008

2. Представить в виде степени и найти значение по таблице:

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

Возведение в степень произведения.

1. Возвести в степень:

2. Найти значение выражения:

д)

1. Возвести в степень:

е)

2. Найти значение выражения:

г)

1. Возвести в степень:

2. Найти значение выражения:

д)

Возведение в степень степени.

1. Возвести в степень:

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

1. Возвести в степень:

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

1. Возвести в степень:

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

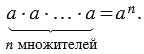
Источник