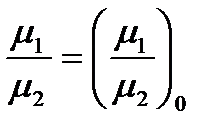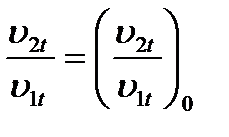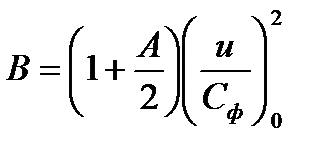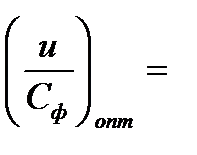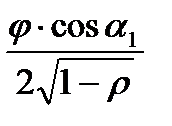Что такое степень реакции ступени

Степень реакции турбинной ступени при переменном режиме работы

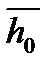
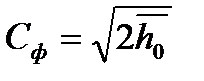
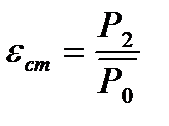
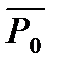
В общем случае режим работы ступени может меняться за счет изменения располагаемого теплоперепада и, следовательно , скорости, отношения давлений , где — давление, соответствующее точке торможения потока, изменение частоты вращения n и, следовательно, окружной скорости u, а так же изменение числа Рейнольдса в ступени, вызванного изменением параметров пара или скорости потока.

Все эти изменения режима работы ступени можно свести к трем переменным – отношению скоростей u/C_ф, отношению давлений ε и фиктивному числу R_еф. Кроме того, могут меняться степень влажности (например, из зоны выше линии насыщения, процесс расширения пара в ступени переходит в зону ниже линии насыщения), а также условия входа в ступень и выхода из нее.

В общем случае все упомянутые режимные параметры меняются одновременно, но нагляднее и удобнее рассмотреть влияние каждого из них на основные характеристики ступени порознь. Начнем это рассмотрение с изменения степени реакции.

Представим, что для какого-то расчетного режима известны все характеристики ступени и ее решеток, в том числе построены (для среднего диаметра) треугольники скоростей. Запишем уравнения неразрывности для выходных сечений сопловой F₁ и рабочей F₂ решеток при докритическом режиме

(1)

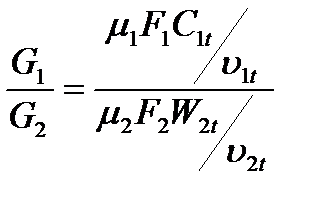
Обозначив все параметры и характеристики ступени при расчетном режиме индексом 0, получим

(2)

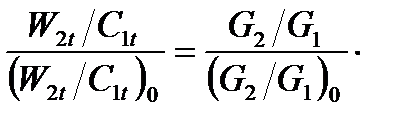
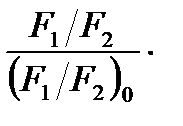
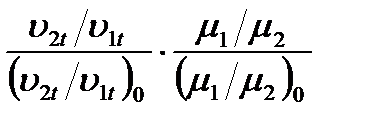
Если считать, что размеры ступени не изменились, т.е. F₁ / F₂ = (F₁ / F₂)₀ и что относительная доля проточек помимо решеток ступени также осталась постоянной, т.е.

(3)

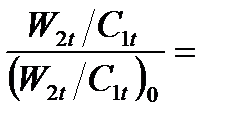
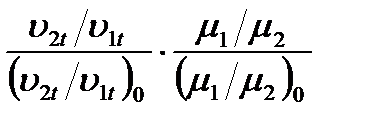
1. Влияние изменения отношения скоростей u/C_ф на степень реакции ρ.

Если предположить, что коэффициенты расхода решеток при изменении u/c_ф и неизменных ε_ст и R_еф остаются постоянными

и в первом приближении принять, что отношение удельных объемов за решеткой также остается постоянным

(4)

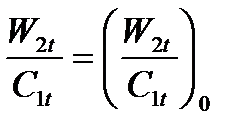
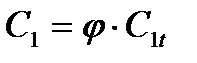
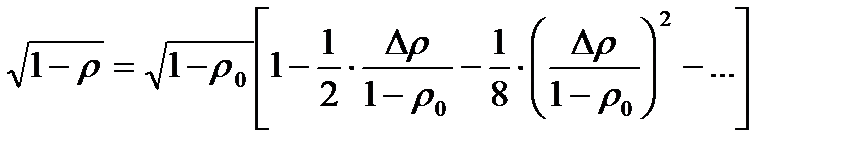
Поскольку при увеличении окружной скорости и неизменной величине и β₁

— рад Тэйлора

ограничимся первыми двумя членами.

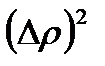
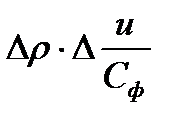
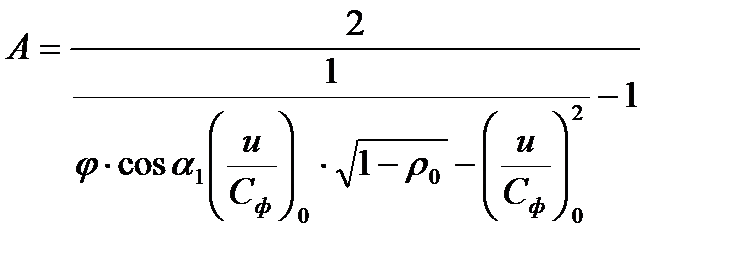
Тогда, пренебрегая членами, содержащими и , и введя коэффициенты

(6)

после ряда преобразований, получили квадратичную зависимость изменения реакции от изменения отношения скоростей

(7)

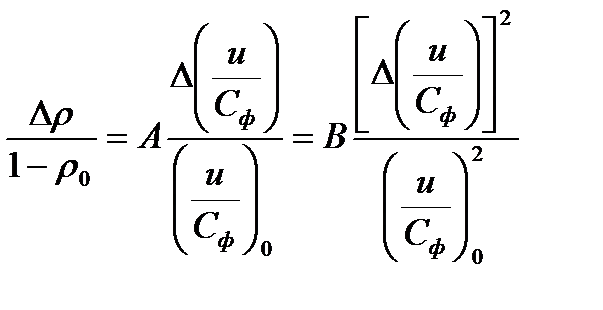
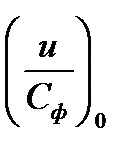
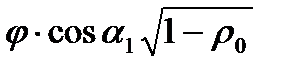
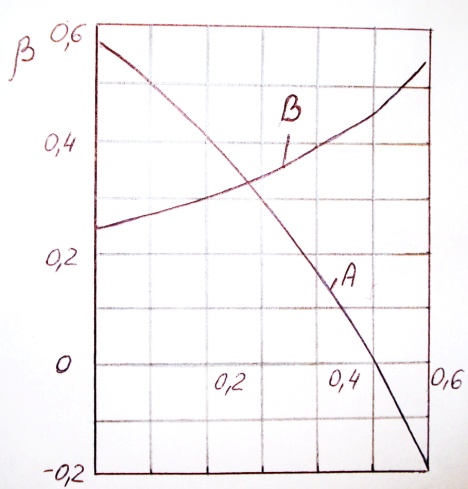
Коэффициенты А и В являются функцией двух параметров и . Приняв, что расчетное отношение скоростей является оптимальным и определяется по формуле

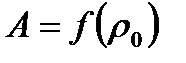
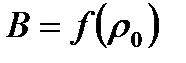
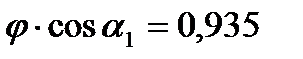
вычислим коэффициенты А и В в зависимости от степени реакции ρ₀. Графически зависимости и при представлены на рисунке

С увеличение расчетной степени реакции ρ₀, т.е. с увеличением расчетного угла β₁₀, коэффициент А уменьшается и при ρ ≈ 0,5 (β₁₀ = 90°) равен А = 0.

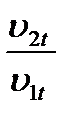
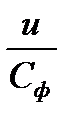
При β₁₀ > 90° коэффициент А 0,7. С увеличением теплоперепада, т.е. с уменьшением ε, отношение удельных объемов растет, следовательно, по (3) увеличивается W_2t, что возможно при соответствующем повышении реакции. При сверхзвуковых скоростях, кроме того, появляется отклонение в косом срезе сопловой решетки, что также вызывает некоторое увеличение степени реакции. Т.о., с уменьшением ε_ст и при неизменном отношении скоростей степень реакции растет, особенно при ε_ст

Дата добавления: 2015-07-22 ; просмотров: 2605 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Лекция_2 «Турбинная ступень. Потери энергии, КПД» _ 2 часа

Рабочие лопатки для повышения надежности против вибрации обычно связываются по вершинам в пакеты ленточным бандажем (по 4-12 лопаток). Поверх бандажа предусматриваются уплотнения для

Рабочие лопатки для повышения надежности против вибрации обычно связываются по вершинам в пакеты ленточным бандажем (по 4-12 лопаток). Поверх бандажа предусматриваются уплотнения для уменьшения утечки пара из области большего давления. Подобное уплотнение устанавливается между диафрагмой и валом.

Полный располагаемый теплоперепад промежуточной ступени:

гдеh₀ = h_0с + h_{0р –} располагаемый теплоперепад ступени по действительным (статическим) параметрам.

h * ₀ = h₀ + X*С 2 ₂/2 – полный располагаемый теплоперепад сопловых лопаток;

С₂ –абсолютная скорость пара на выходе из предыдущей ступени;

где h * _0с и h * _0с располагаемые теплоперепады сопловых лопаток;

Если степень реакции р = 0, то турбинная ступень называется чисто активной и, следовательно, в такой ступени весь теплоперепад срабатывается в сопловых решетках.

Когда р невелика (до 0,2 – 0,25), то ступень принято называть также активной. Иногда такую ступень называют активной с небольшой степенью реакции.

В многоступенчатой турбине степень реакции изменяется в широких пределах, возрастая от первой до последней ступени. Так для конденсационной турбины величина р на первых ступенях принимается в пределах 0,06 – 0,15, а на последних двух-трех ступенях достигает 0,40 – 0,65.

Геометрия турбинной ступени –рис. выше определяется сечением и цилиндрическими сечениями (развертками) на одном или нескольких диаметрах

Развертка цилиндрического сечения одного ряда лопаток называется решеткой профилей. На радиусе У она характеризуется формой и размерами самого профиля и канала, образуемого соседними профилями.

Профилем лопатки (рис.выше) называется ее сечение, перпендикулярное радиусу. Средняя линия профиля проходит через центры окружностей, вписанных в профиль. Обычно за хорду профиля ___ принимают расстояние между концами средней линии профиля. Толщина профиля С измеряется по перпендикуляру к его средней линии. Часто величина С отсчитывается по перпендикуляру к хорде профиля. Наибольшая толщина С_махявляется характерным параметром профиля. Радиусы закруглений входной и выходной кромок профиля обозначаются буквой r. Максимальной вогнутостью профиля f_max называется наибольшее расстояние от хорды до средней линии профиля.

Сравнительную оценку различных профилей производят по относительным величинам. За определяющий параметр принимается хорда ____. В результате получим относительную толщину профиля C = C_max/____.

которые при докритических скоростях принимаются равными углам потока а 1 и a i- Положение профилей в решетках определяется уг­лами установки а_у и f)_y, образуемыми хордой и фронтальной линией. Углы аог и Рт, характеризующие направления входных кромок профилей, называются геометрическими (входными) углами. Иногда эти углы называются скелетными. Углы изогнутости профилей

Из термодинамики известно, что абсолютный (термический) КПД идеальной ПТУ с конденсатором без учета работы питательного насоса, представляется отношением:

к.п.д. = Но/qo

т.е. разность начальной и конечной энтальпии при изоэнтропном расширении пара см. рис. 1.5.

В действительности из-за потерь ∑Ah_i = h_k – h_ktназывав емых внутренними, процесс расширения пара в турбине происходит не по изоэнтропе OK_t, а по политропе GK, в результате чего использованный (внутренний) теплоперепад:

при этом энтальпия h_K определяет состояние пара в конце политропного (действительного) процесса расширения.

Отношение использованного теплоперепада к располагаемому называется относительным внутренним КПД турбины:

Источник

Понятие о степени реакции

Возьмем некоторую к-ю турбинную ступень у которой:

Р_о – давление пара перед ступенью;

t_o – температура пара перед ступенью;

С_2(к-1) – скорость пара на входе в направляющий аппарат;

Р_d – давление за направляющим аппаратом;

Р₁ – давление за ступенью.

Обратимся к диаграмме h-s (рис.15.). На пересечении изобары Р_о и изотермы t_o находим точку А_о, определяющую состояние пара перед ступенью. Если бы процесс течения пара через ступень происходил без трения, то он изобразился адиабатой А_оА_dtА_1t. Разность энтальпий в точках А_о и А_1t определит адиабатный теплоперепад на турбинную ступень:

Адиабатный теплоперепад на ступень h_a характеризует запас потенциальной энергии пара, который может быть преобразован в данной ступени в полезную работу. Кроме того, на входе в ступень пар уже обладает запасом кинетической энергии .

Таким образом, полный запас энергии, который может быть преобразован в данной ступени в полезную работу, определится суммой адиабатного теплоперепада и входной кинетической энергии пара.

Эта сумма называется располагаемым адиабатным теплоперепадом на ступень:

(3.32)

Работа на окружности (полезная работа совершаемая турбинной ступенью), обозначаемая символом L_и, может быть рассчитана как разность располагаемой энергии и потерь энергии в турбинной ступени. Для подсчета потерь рассмотрим процесс течения в направляющем аппарате и на рабочих лопатках турбинной ступени.

Точка А_dt характеризует состояние пара в конце адиабатного расширения в направляющем аппарате. Таким образом, можно определить адиабатные теплоперепады и .

=h_o-h_dt (3.33)

= + (3.34)

Однако, при течении пара через направляющий аппарат ступени наблюдаются потери энергии q_d; за счет этих потерь энтальпия пара за направляющим аппаратом увеличивается и составляет

На пересечении изобары Р_d и линии h=const найдется точка А_d, характеризующая действительное состояние пара; процесс в направляющем аппарате изобразится отрезком политропы А_оА_d.

Далее пар поступает на рабочие лопатки ступени. Если бы процесс на рабочих лопатках происходил без потерь, он изобразился бы отрезком адиабаты А_dА_st. Таким образом, адиабатный теплоперепад на рабочих лопатках h_as составит:

Однако, на рабочих лопатках наблюдаются потери энергии q_s; за счет этих потерь энтальпия пара за рабочими лопатками увеличивается и составляет

На пересечении изобары Р₁ и линии h_s = const найдется точка А_s, характеризующая действительное состояние пара; процесс на рабочих лопатках изобразится отрезком политропы А_dА_s.

На входе из ступени пар имеет «абсолютную» скорость. Таким образом, покидая ступень, пар уносит с собой кинетическую энергию . Эта энергия не может быть преобразована в полезную работу в данной ступени и поэтому для данной ступени она потеряна. Энергия называется потерей с выходной скоростью или просто выходной потерей:

q_a= (3.38)

Выйдя из ступени со скоростью С₂, поток пара либо плавно войдет в направляющий аппарат следующей ступени, либо просто будет заторможен; для рассматриваемой ступени дальнейшая судьба пара безразлична. Поэтому будем считать, что происходит торможение пара при постоянном давлении Р₁, за счет чего энтальпия пара увеличивается. Таким образом, энтальпия пара за ступенью составит

Точка А_d, характеризующая состояние пара за ступенью, найдется на пересечении изобары Р₁ и линии h_а=const. Отрезок изобары А_sА_a, характеризует торможение пара за ступенью.

Итак, мы установили, что процесс преобразования энергии в ступени сопровождается следующими потерями энергии:

– потери в направляющем аппарате q_d;

– потери на рабочих лопатках q_s;

– потери с выходной скоростью q_a.

Эти потери называются потерями на окружности турбинной ступени.

Тогда работа на окружности L_u может быть определена как разность между располагаемой энергией и потерями на окружности:

Иногда входная энергия пренебрежительно мала, тогда h_а≈ h’_а и потому

Подсчитанная по формуле (3.40 и 3.41) может быть показана непосредственно на диаграмме h-s (рис.15, 16 и 17).

Из рассмотренного в диаграмме h-s процесса (рис.15) вытекает, что часть h_аd общего теплоперепада на ступень h_а срабатывается в направляющем аппарате, а часть h_аs – в рабочих лопатках. Для оценки распределение теплоперепадов по венцам вводится понятие степени реакции ступени.

Степенью реакции ρ условимся определять отношением теплоперепада h_аs на рабочих лопатках к сумме теплоперепадов на направляющем h_аd и рабочем h_аs венцах:

(3.42)

Теперь можно дать более строгие определения введенных ранее понятий активной и реактивной ступеней.

Если ρ=0, а следовательно, h_аs=0, то ступень называется активной турбинной ступенью (процесс расширения пара в диаграмме h-s показан на рис.16, где изобара Р_d совпадает с изобарой Р₁ и теплоперепад h_аs станет равным нулю).

Если ρ≈ 0,5, а следовательно, h_аs=h_аd, то ступень называется реактивной турбинной ступенью (процесс расширения пара в диаграмме h-s показан на рис.15).

В настоящее время часто применяются ступени, у которых 0 а), то ускорение потока происходит в каналах расходящейся формы. В этом случае говорят о сверхзвуковой скорости пара и сверхкритическом режиме течения.

Совершенно очевидно, что для получения сверхзвуковых скоростей на выходе из решетки её каналы вначале должны быть сходящимися, а затем – расходящимися (рис.18). В узком сечении канала скорость течения равна местной скорости звука. Это сечение называется критическим. Критическими параметрами пара называют такие параметры пара, при которых скорость парового пара равна местной скорости звука.

Поставим задачу: определить критическое давление пара. Запишем уравнение энергии для входного и критического сечений. Критические параметры будем обозначать индексом «*».

(3.46)

Если ввести в рассмотрение параметры торможения – давление и удельный объем , то левая часть уравнения (2.3.3) запишется в виде:

(3.4 7)

Запишем, что скорость равна местной скорости звука, и потому

Подставляя значение в (2.3.3), получим:

(3.48)

Если предположить, что изменение состояния пара при течении от входного до критического сечений происходит по адиабате, то

Подставляя значение в (.3.48), получим выражение для отношения критического давления к начальному давлению . Это отношение обозначим и будем называть критическим отношением давлений:

(3.49)

Из (.3.49) видим, что величина критического отношения давлений не зависит от величины параметров пара, а зависит только от его физических свойств (природы рабочего тела).

Для перегретого пара = 0,546. Для насыщенного пара = 0,577.

Таким образом, зная давление пара перед решеткой и за решеткой, можно сразу решить вопрос о характере течения пара в каналах решетки.

Если (для рабочей решетки ), то ни в одном из сечений канала не будут достигнуты критические параметры пара; в этом случае скорость пара за решеткой будет дозвуковой, а каналы решетки должны быть сходящимися.

Если (для рабочей решетки ), то в узком сечении межлопаточных каналов будут достигнуты критические параметры пара, а если за узким сечением имеется расходящаяся часть канала, то за решеткой следует ожидать появления сверхзвуковых скоростей.

Источник