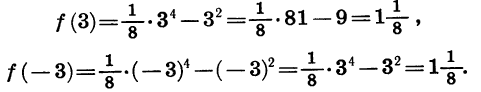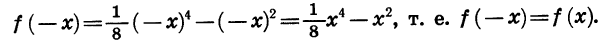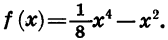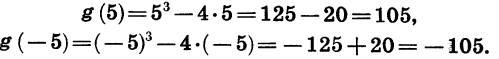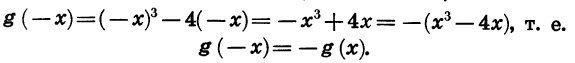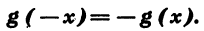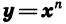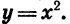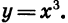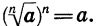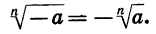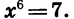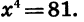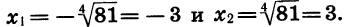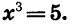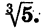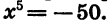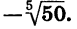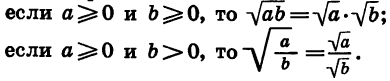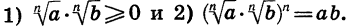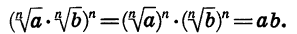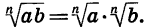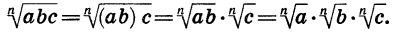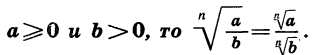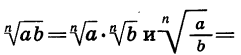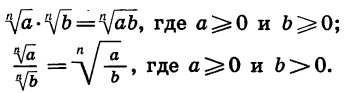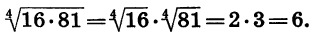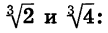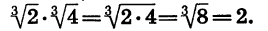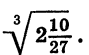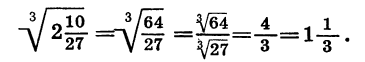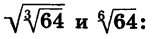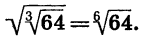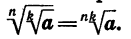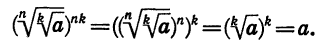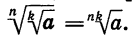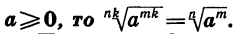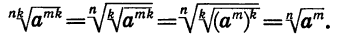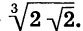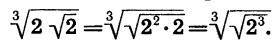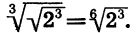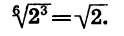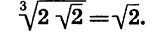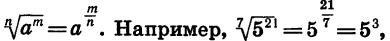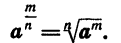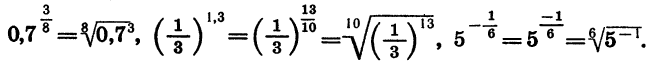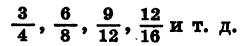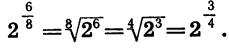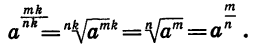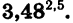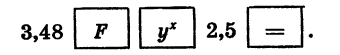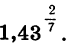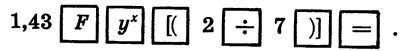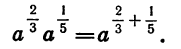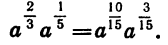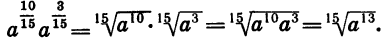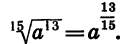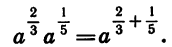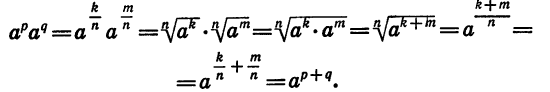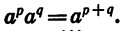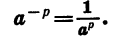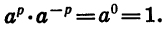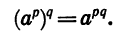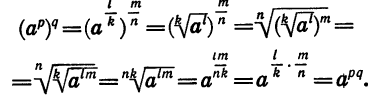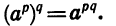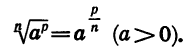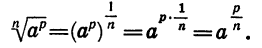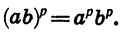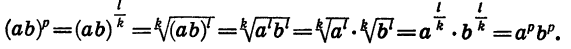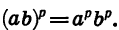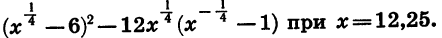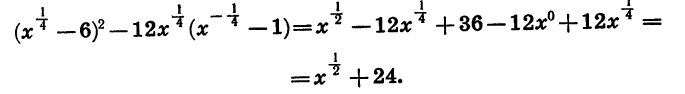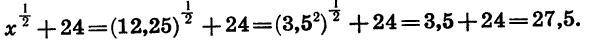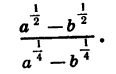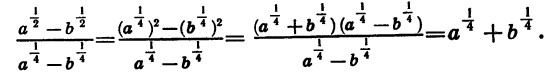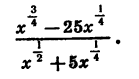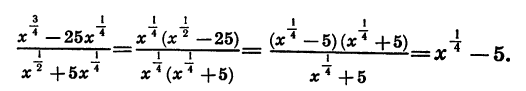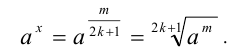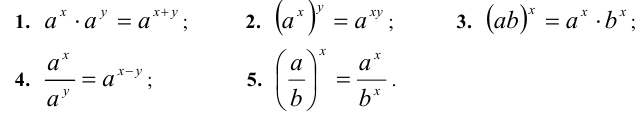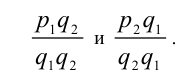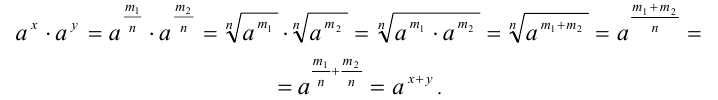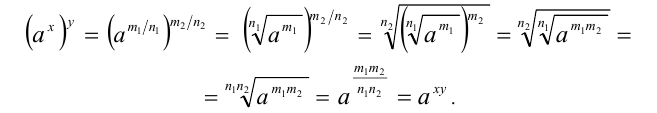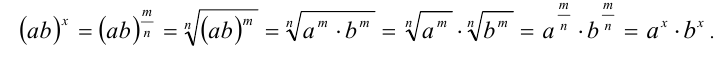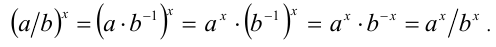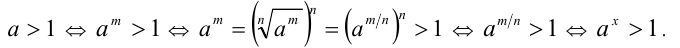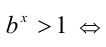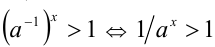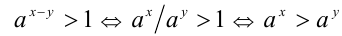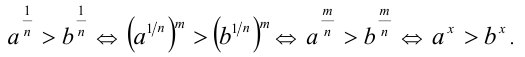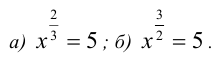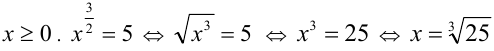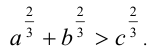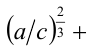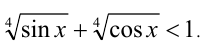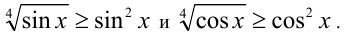Что такое степень с рациональным показателем определение
Алгебра
А Вы уже инвестируете?
Слышали про акцию в подарок?
Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб
План урока:
Степень с рациональным показателем
Напомним, что в 7 классе мы впервые познакомились с понятием степени, причем тогда рассматривались случаи, когда показателем степени является натуральное число. В 8 классе понятие степени было расширено, теперь в него включались случаи, когда показатель являлся целым числом. Настоятельно рекомендуем перечитать соответствующие уроки. Сегодня же мы можем сделать ещё один шаг вперед и рассмотреть степени с рациональными показателями.
При расширении понятия степени важно обеспечить то, чтобы уже известные правила работы с целыми степенями работали и для дробных показателей. Одно из свойств степеней выглядит так:
Подставим в эту формулу следующие значения переменных:
Мы специально выбрали эти числа такими, чтобы произведение mn равнялось единице:
Подставляем эти значения:
(3 1/6 ) 6 = 3 1/6 • 6 = 3 1 = 3
Однако по определению корня n-ой степени число, дающее при возведении в шестую степень тройку, является корнем шестой степени из трех. То есть можно записать:
С помощью подобных преобразований нам удалось указать, чему равно число, возведенное в дробную степень. Аналогично можно показать, что для любого а > 0 справедлива формула:
Действительно, если возвести левую часть в n-ую степень, то получим:
(а 1/ n ) n = a 1/ n • n = a
Значит, по определению корня n-ой степени
Ограничение а > 0 необходимо для того, чтобы не рассматривать случаи, когда подкоренное выражение является отрицательным.
C учетом этого выполним преобразование:
В результате несложных преобразований нам удалось получить формулу, позволяющую возводить число в степень, у которой рациональный показатель!
Приведем несколько примеров вычисления дробных степеней:
Часто при вычислениях удобнее сначала извлечь корень из числа, а потом полученный результат возвести в степень:
Напомним, что одну и ту же дробь можно представить разными способами, например:
1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 0,5
Возникает вопрос – изменится ли значение дробной степени, если мы приведем дробь к новому знаменателю? Очевидно, что нет, но всё же убедимся в этом на примере. Сначала возведем в степень 1/2 число 25:
Теперь заменим дробь 1/2 на идентичную ей дробь 2/4:
Согласитесь, возводить число 81 в 25-ую степень не очень легко! Поэтому поступим иначе. Сократим дробь 25/100:
0,25 = 25/100 = 25/(25•4) = 1/4
Теперь вычисления будет более простыми:
Вообще легко запомнить, что 0,25 = 1/4, а 0,5 = 1/2. Замена десятичных дробей обыкновенными дробями сильно упрощает вычисления. Приведем примеры:
Свойства дробных степеней и операции с ними
Когда мы изучали степени с целыми показателями, мы выяснили, что правила работы с ними ничем не отличаются от правил работы со степенями с натуральным показателем. Оказывается, эти же правила работают и для степеней с рациональным показателем. Сформулируем основные свойства дробных степеней.
Например, справедливы следующие действия:
5 0,5 •5 2,5 = 5 0,5 + 2,5 = 5 3 = 125
19 5/3 •19 1/3 = 19 5/3 + 1/3 = 19 2 = 361
29,36 –0,37 •29,36 1,37 = 29,36 –0,37 + 1,37 = 29,36 1 = 29,36
Вот несколько примеров подобных вычислений:
17 4,5 :17 3,5 = 17 4,5–3,5 = 17 1 = 1
4 9,36 :4 6,36 = 4 9,36–6,36 = 4 3 = 64
20 12 :20 14 = 20 12–14 = 20 –2
Проиллюстрируем это правило примерами:
(6 0,25 ) 8 = 6 0,25•8 = 6 2 = 36
(9 3/2 ) 2 = 9 (3/2)•2 = 9 3 = 729
(25 4 ) 0,125 = 25 4•0,125 = 25 0,5 = 5
Покажем, как можно применять данное правило:
4 1/6 •16 1/6 = (4•64) 1/6 = 64 1/6 = 2
0,5 1,5 •50 1,5 = (0,5•50) 1,5 = 25 1,5 = 25 1+0,5 = 25 1 •25 0,5 = 25•5 = 125
4,9 0,5 •10 0,5 = (4,9•10) 0,5 = 49 0,5 =7
Это правило можно применять следующим образом:
360 0,5 :10 0,5 = (360:10) 0,5 = 36 0,5 = 6
500 3 :50 3 = (500:50) 3 = 10 3 = 1000
6,25 1/4 :0,01 1/4 = (6,25:0,01) 1/4 = 625 1/4 = 5
Заметим, что степени очень удобны тем, что с их помощью легко упростить работу с корнями, ведь если
то верное и обратное:
То есть любое выражение с корнями в виде степени с рациональным показателем.
Пример. Вычислите значение выражения
Решение. Корней много, поэтому для удобства заменим их степенями
Получили тоже самое выражение, но в более компактном виде. Посчитаем его значение:
(9 1/4 ) 1/5 •3 9/10 = (9 0,25 ) 0,2 •3 0,9 = 9 0,25•0,2 •3 0,9 = 9 0,05 •3 0,9 = (3 2 ) 0,05 •3 0,9 =
=3 2•0,05 •3 0,9 = 3 0,1 •3 0,9 = 3 0,1•0,9 = 3 1 = 3
Пример. Упростите выражение
(81 n+1 – 65•81 n ) 0,25
Решение. Степень 81 n+1 можно представить как произведение:
81 n+1 = 81 n •81 1 = 81•81 n
С учетом этого можно записать:
(81 n+1 – 65•81 n ) 0,25 = (81•81 n – 65•81 n ) 0,25 = (81 n (81 – 65)) 0,25 =
= (81 n •16) 0,25 = 81 0,25 n •16 0,25 = 81 0,25 n •16 1/4 = 2•81 0,25 n
Сравнение степеней
Напомним, что из двух корней n-ой степени больше тот, у которого больше подкоренное выражение:
Отсюда следует вывод, что если a 1/ n 1/ n
теперь возведем каждую часть этого неравенства в степень m. Тогда получим неравенство:
Получили, что из двух степеней с одинаковыми показателями меньше та, у которой меньше основание (правила сравнения будем нумеровать, чтобы на них удобнее было ссылаться):
В частности, справедливы следующие неравенства:
Здесь мы рассматривали случаи, когда показатель степени является положительным числом. А что делать, если он отрицательный? Тогда степень следует «перевернуть», воспользовавшись уже известной вам формулой:
Пример. Сравните выражения с рациональным показателем степени:
20 –3,14 и 50 –3,14
Решение. Избавимся от знака минус в показателе:
20 –3,14 = (1/20) 3,14 = 0,05 3,14
50 –3,14 = (1/50) 3,14 = 0,02 3,14
Получили две степени с одинаковым и, что принципиально важно, положительным показателем. Из них больше та, у которой больше основание. То есть из неравенства 0,02 3,14 3,14
Особенным является случай, когда показатель степени равен нулю. Напомним, что любое число в нулевой степени (кроме самого нуля) равно единице, а выражение 0 0 не имеет смысл. Это значит, что числа в нулевой степени равны друг другу, даже если у них разные основания:
18,3546 0 = 12,3647 0 = 1
Несколько сложнее сравнивать числа, у которых одинаковые основания, но различные показатели. Здесь возможны три случая – основание либо равно единице, либо больше неё, либо меньше неё.
На основании этого правила можно записать, что:
Единица в любой степени равна самой себе. Поэтому, если у двух чисел в основании записана именно она, то они должны быть равны друг другу:
1 –7,56 = 1 –0,15 = 1 0,236 = 1 521,36 = 1
0,5 = 1/2 = 1/(2 1 ) = 2 –1
0,5 7,6 = (2 –1 ) 7,6 = 2 –7,6
0,5 8,9 = (2 –1 ) 8,9 = 2 –8,9
Такие числа мы уже умеем сравнивать. Так как
Например, справедливы неравенства:
0,57 15,36 > 0,57 16,47
Рассмотрим чуть более сложное задание на сравнение степеней, где надо использовать одновременно несколько правил.
Пример. Докажите, что
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3
Решение. Напрямую вычислить значение выражений в правой и левой части затруднительно. Однако мы можем усиливать неравенство, чтобы получить более простые выражения.
Усилить неравенство – это значит увеличить его меньшую или уменьшить большую часть. Например, неравенство 10 1/3 :
Также ясно, что 27 1/3 1/3 (правило 1). Усилим исходное неравенство:
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 (1)
Действительно, если (1) справедливо, то мы можем записать двойное неравенство
0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 1/3
Опустив здесь среднюю часть, получим исходное неравенство. Так как 27 1/3 = 3, мы можем переписать (1) так:
0,9 0,9 + 0,8 0,8 + 0,7 0,7 0,8 0,8 (снова используем правило 1). С другой стороны, 0,9 0,8 0,7 (правило 3). Значит, можно записать двойное неравенство:
Их левые части стоят в (2). Следовательно, можно усилить (2):
0,9 0,7 + 0,9 0,7 + 0,9 0,7 0,7 0,7 0,7 :
Из правила 1 следует, что (4) справедливо. Но мы получили его, усиливая исходное неравенство. Из справедливости более сильного неравенства следует и справедливость более слабого. Следовательно, из справедливости (4) вытекает верность исходного неравенства, которое и надо было доказать.
Степень с рациональным показателем в математике с примерами решения и образцами выполнения
Степень с рациональным показателем — это степень в показателе которой находится конечная обыкновенная или десятичная дробь.
Любую степень с рациональным показателем можно представить в виде корня, чья степень будет равна знаменателю дроби, находящейся в показателе степени, а числитель будет степенью подкоренного выражения.
Степенная функция
Четные и нечетные функции:
Сравним значения функции 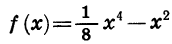
Мы видим, что f (- 3) = f(3). Значения этой функции равны и при любых других противоположных значениях аргумента. Действительно,
При этом рассматриваемая функция такова, что для каждого значения аргумента х противоположное ему число — х также принадлежит ее области определения. В таких случаях говорят, что область определения функции симметрична относительно нуля.
Функции, обладающие такими свойствами, называют четными функциями.
Определение:
Функция y = f(х) называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство
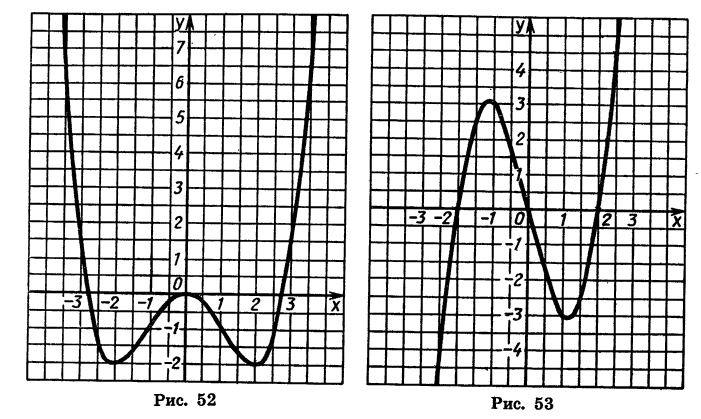
На рисунке 52 построен график функции
График этой функции симметричен относительно оси у.
При этом область определения функции g симметрична относительно нуля.
Функции, обладающие такими свойствами, называют нечетными функциями.
Определение:
Функция y = g (х) называется нечетной, если область ее определения симметрична относительно нуля и для любого значения аргумента х верно равенство
На рисунке 53 построен график функции 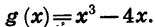
С примерами четных и нечетных функций мы уже встречались. Так, функции, заданные формулами 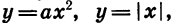
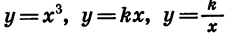
Заметим, что не всякая функция является четной или нечетной. Например, каждая из функций 
Функция
Рассмотрим функцию, заданную формулой 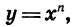
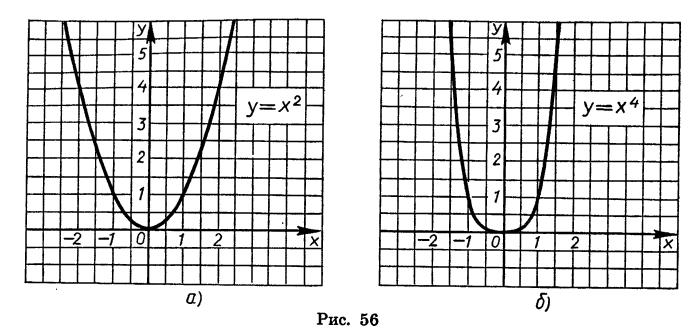
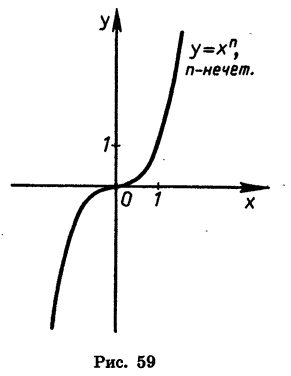
Степенные функции при я = 1, 2 и 3, т. е. функции у = х, 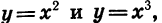
Выясним теперь свойства степенной функции и особенности ее графика при любом натуральном n.
Выражение 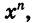
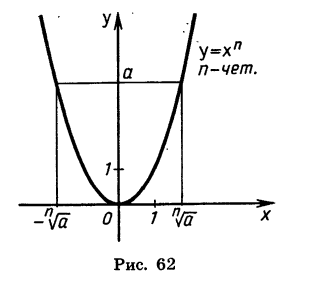
Сначала рассмотрим случай, когда показатель п — четное число. Свойства функции 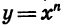
Действительно, пусть 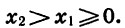
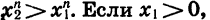


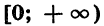
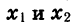
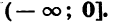
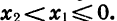
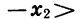
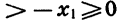


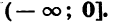
5. Область значений функции есть множество неотрицательных чисел.
Мы установили, что при любом х и четном n функция принимает неотрицательные значения. Можно доказать, что любое неотрицательное число является значением степенной функции с натуральным показателем при некотором 
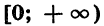

нечетном n. Эти свойства аналогичны свойствам функции
число является значением степенной функции с натуральным показателем при некотором 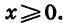
На рисунке 58 изображены графики функций 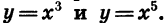
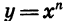
Определение корня n-й степени:
Напомним, что квадратным корнем из числа о называется такое число, квадрат которого равен а. Аналогично определяется корень любой натуральной степени n.
Корнем n-й степени из числа а называется такое число, n-я степень которого равна а.
Рассмотрим степенную функцию 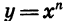
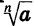
Запись 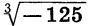
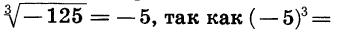
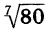
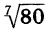
Рассмотрим теперь степенную функцию 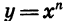
Другими словами, если n — четное число и а > 0, то существуют два корня n-й степени из а. Эти корни являются противоположными числами. Если а = 0, то корень n-й степени из а равен нулю. Если а 0) записывают так: 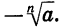
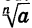
Если n = 2, то показатель корня не пишется.
Итак, если n — нечетное число, то выражение 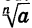
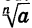
Из определения корня n-й степени следует, что при всех значениях а, при которых выражение 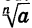
Выражение 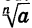

Определение:
Арифметическим корнем n-й степени из неотрицательного числа а называется неотрицательное число, n-я степень которого равна а.
Вообще при любом положительном а и нечетном n
С помощью знака корня n-й степени записываются решения уравнений вида 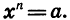
Пример:
Решим уравнение
Корнями уравнения служат числа, шестая степень которых равна 7. Таких чисел два: 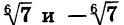
Пример:
Решим уравнение
Уравнение имеет два корня:
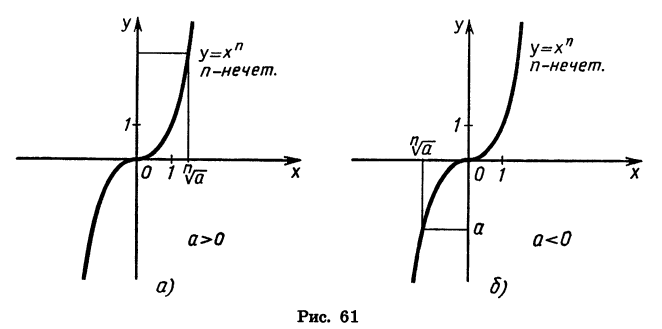
Пример:
Решим уравнение
Уравнение имеет единственный корень (см. рис. 61). Этот корень есть число, третья степень которого равна 5, т. е.
Пример:
Решим уравнение
Уравнение имеет единственный корень (см. рис. 61). Этот корень есть число, пятая степень которого равна —50, т. е. 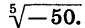
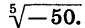
Свойства арифметического корня n-й степени
Нам известны следующие свойства арифметического квадратного корня:
Аналогичными свойствами обладает арифметический корень n-й степени и при n > 2.
Теорема:
Если 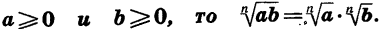
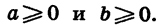
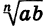
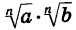
Значение выражения 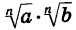
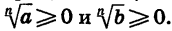
Значит, по определению арифметического корня n-й степени верно равенство
Доказанная теорема распространяется на случай, когда число множителей под знаком корня больше двух. Например, если 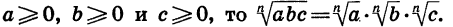
Таким образом, арифметический корень п-й степени обладает свойством: корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Теорема:
Если
Доказательство проводится аналогично доказательству теоремы 1.
Итак, справедливо еще одно свойство арифметического корня n-й степени: корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Поменяв местами в каждом равенстве 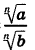
Приведем примеры применения доказанных свойств.
Пример:
Найдем значение выражения 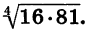
Пример:
Перемножим корни
Пример:
Найдем значение выражения
Пользуясь теоремой о корне из дроби, получаем:
Рассмотрим другие свойства корня n-й степени. Начнем с примера. Сравним значения выражений
Мы видим, что значения этих выражений равны, т. е.
Теорема:
Если п и к — натуральные числа и
Так как 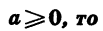
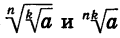
Следовательно, по определению арифметического корня верно равенство
Теорема:
Если n, k и m — натуральные числа и
По теореме 3 имеем:
Мы доказали, что арифметический корень n-й степени обладает свойством: если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
Это свойство иногда называют основным свойством корня. Приведем пример применения теорем 3 и 4.
Пример:
Внесем множитель 2 под знак квадратного корня. Получим:
По теореме о корне из корня имеем:
Применив основное свойство корня, получим:
Степень с рациональным показателем и ее свойства
Определение степени с дробным показателем
Мы знаем, какой смысл имеет выражение 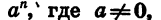
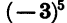
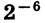
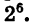
Из определения арифметического корня следует, что если m — целое число, n — натуральное и m делится на n, то при а > 0 верно равенство
Так как 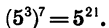
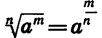
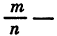
Определение:
Если а — положительное число, 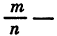
По определению имеем:
Степень с основанием, равным нулю, определяется только для положительного дробного показателя: если 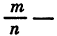
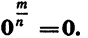
Мы знаем, что одно и то же дробное число можно представить в виде дроби с целым числителем и натуральным знаменателем разными способами. Например, дробное число 0,76 можно представить в виде дроби так:
Значение степени с дробным показателем r не зависит от способа записи числа r в виде дроби: представляя r в виде отношения целого числа к натуральному разными способами, всегда будем получать один и тот же результат. Например:
Покажем это в общем случае.
Пусть а > 0, m — целое, n и k — натуральные числа. Пользуясь определением степени с дробным показателем и основным свойством корня, получим:
Значения степеней с дробным показателем и положительным основанием можно находить приближенно с помощью инженерного микрокалькулятора, например, «Электроника БЗ-Зб». Микрокалькулятор «Электроника Б3-36» имеет 25 клавиш, из них 22 клавиши можно использовать для выполнения двух операций. Одна операция обозначена на самой клавише, а другая написана над ней. При выполнении операций, обозначенных на клавишах, микрокалькулятор работает в нормальном режиме, а когда производят операции, обозначенные над клавишами, то микрокалькулятор работает в совмещенном режиме. Чтобы перейти к этому режиму, надо нажать клавишу 
Пример:
Найдем значение степени
Вводим основание степени у, равное 3,48, нажимаем клавишу 
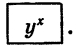
равный 2,5, и клавишу 
Выполнив вычисления, найдем, что приближенное значение степени 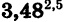
Пример:
Вычислим значение степени
Этот пример отличается от примера 1 тем, что показатель степени представлен не в виде десятичной дроби, а в виде обыкновенной дроби. Поэтому после введения основания степени 1,43 надо и нажатия клавиш 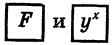
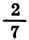

Выполнив вычисление, получим 1,1075969.
Заметим, что в тех случаях, когда результат вычислений по модулю оказывается меньше 0,0000001 или больше 99 999 999, микрокалькулятор дает ответ в виде 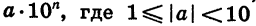
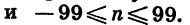
Свойства степени с рациональным показателем
Известные нам свойства степени с целым показателем справедливы и для степени с любым рациональным показателем. Перечислим их.
Для любого а > 0 и любых рациональных чисел р и q:
Для любых а >0 и b > 0 и любого рационального числа р:
Докажем свойство (1). Сначала покажем на частном примере способ доказательства этого свойства.
Пусть, например, 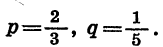
Приведем дроби 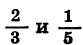
Так как 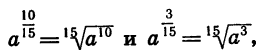
Переходя к степени с дробным показателем, получим:
Следовательно, 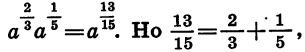
Проведем теперь доказательство свойства (1) в общем виде. Представим рациональные числа р и q в виде дробей с одинаковыми знаменателями: 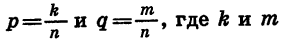
Значит,
Из свойства (1) следует, что для любого положительного а и любого рационального числа р
Действительно,
Свойство (2) следует из свойства (1) и определения частного. Докажем свойство (3), т. е. докажем, что при а > 0 и любых рациональных р и q
Пусть 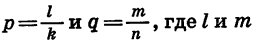
Значит,
Покажем, что при любом рациональном р и любом натуральном n
Действительно, по определению степени с дробным показателем и свойству (3) имеем:
Докажем свойство (4), т. е. докажем, что при а > 0 и b > 0 и любом рациональном р
Пусть 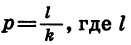
Значит,
Свойство (5) можно доказать, представив дробь 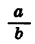
Преобразование выражении, содержащих степени с дробными показателями
Рассмотрим примеры, в которых используются тождественные преобразования выражений, содержащих степени с дробными показателями.
Пример:
Найдем значение выражения
Предварительно упростим это выражение:
Подставим в выражение 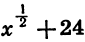
Пример:
Представим числитель 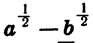
Пример:
Разложим на множители числитель и знаменатель дроби. Получим
Степени с рациональными показателями
Пусть а — положительное действительное число, x — произвольное рациональное число, т.е. число, представимое в виде несократимой обыкновенной дроби 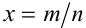
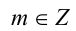
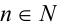
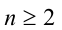
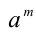
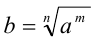
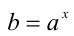
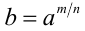
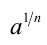
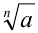
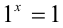
Если основание а = 0, то рациональная степень определена только при положительном показателе 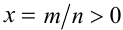
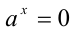
Степень с рациональным показателем можно определить и для отрицательного основания. Пусть 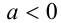
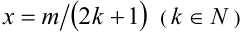
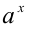
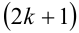
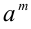
В этом случае справедливы все перечисленные ниже свойства степеней с рациональными показателями, которые доказываются аналогично.
Большинство свойств степеней с рациональными показателями выглядят аналогично (хотя являются обобщением) соответствующим свойствам степеней с целыми показателями. Доказательство свойств степеней с рациональными показателями проведём для случая положительного основания. В выполнении свойств степеней для случаев нулевого и отрицательного оснований убедитесь самостоятельно.
Свойства степеней с рациональными показателями
Пусть а и b — положительные действительные числа, а x и у — рациональные числа. Тогда верны следующие равенства:
6.Пусть 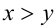
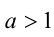
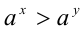
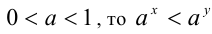
7.Если 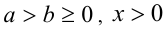
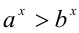
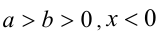
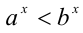
Доказательство:
Рассмотрим два рациональных числа 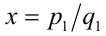
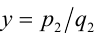
Поэтому будем считать при доказательстве этого свойства, что рациональные числа x и у уже представлены в виде двух дробей с одинаковыми знаменателями: 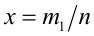
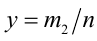
Пусть 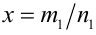
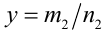
Пусть 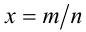
Воспользуемся доказанными свойствами 3 и 2 степеней с рациональным показателем:
Докажем вначале два вспомогательных свойства:
1) если 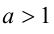
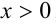
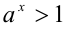
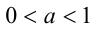
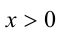
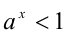
1) Пусть 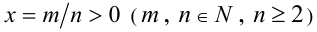
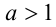
свойством 8 числовых неравенств и определением степени с рациональным показателем:
2) Пусть теперь 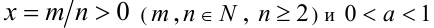
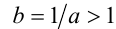
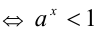
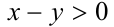
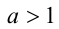
Доказательство в случае 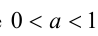
7.Пусть 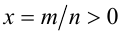
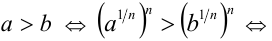
Замечание. Мы доказали более сильное утверждение, а именно: если 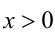
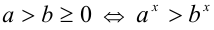
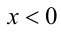
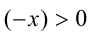
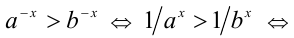
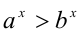
Пример:
Решить уравнения:
Решение:
а) ОДЗ:
б) ОДЗ:
Пример:
Доказать, что если 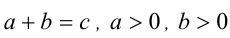
Складывая почленно два последних неравенства, получаем, что 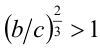
Пример:
Решить неравенство
Решение:
Так как на ОДЗ 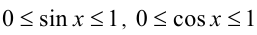
Складывая эти неравенства, получаем, что на ОДЗ 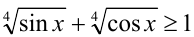
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института