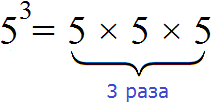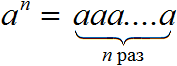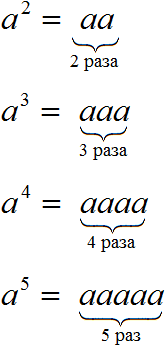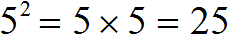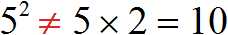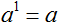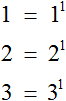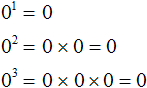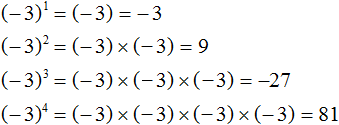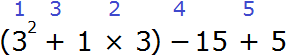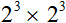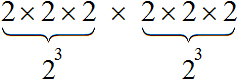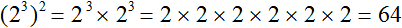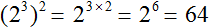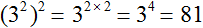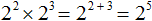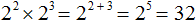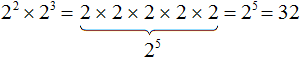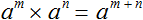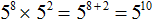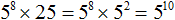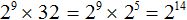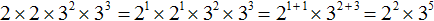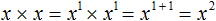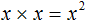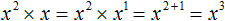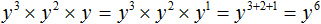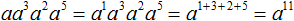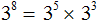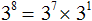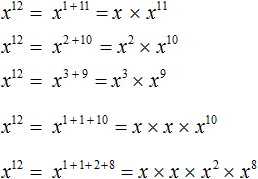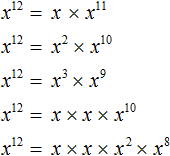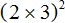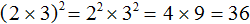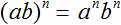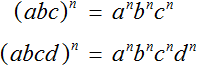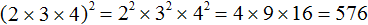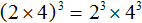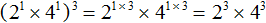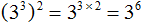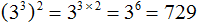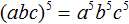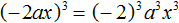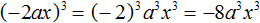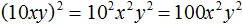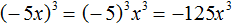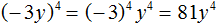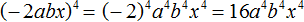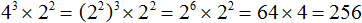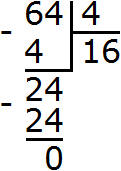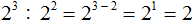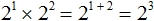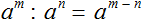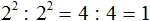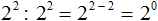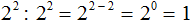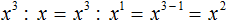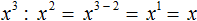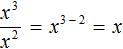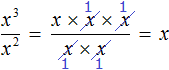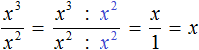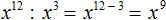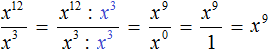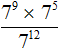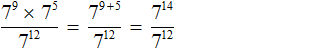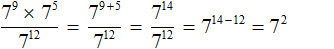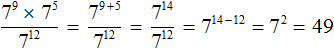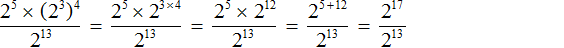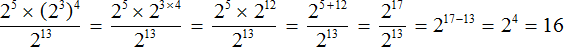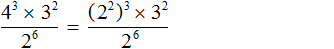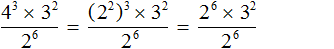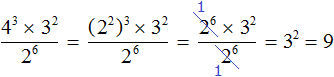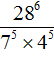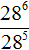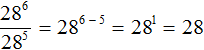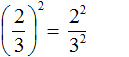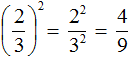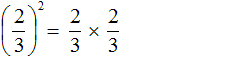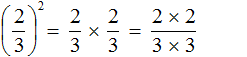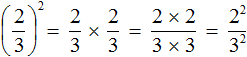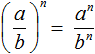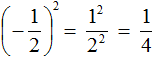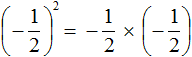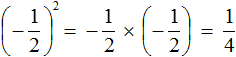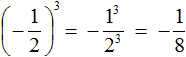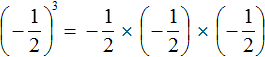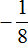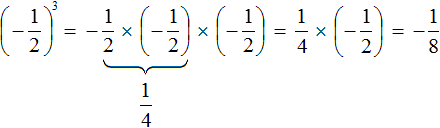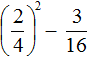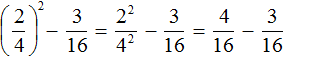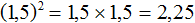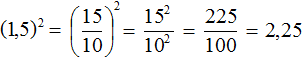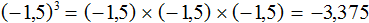Что такое степень сравнения в математике

Сравнение чисел при решении уравнений, неравенств и задач с модулями

При решении уравнений и неравенств, а также задач с модулями требуется расположить найденные корни на числовой прямой.

Как ты знаешь, найденные корни могут быть разными.

А могут быть и вот такими: \( \sqrt<6>\), \( \left( 4-\sqrt <3>\right)\), \( \frac<\sqrt[6]<6>><\sqrt<13>+\frac<4><13>>\).

Если числа не рациональные, а иррациональные, или представляют собой сложные математические выражения, то расположить их на числовой прямой весьма проблематично.

Для этого нужно уметь их сравнивать.

Калькуляторами на экзамене пользоваться нельзя, а приближенный подсчет не дает 100% гарантий, что одно число меньше другого (вдруг разница между сравниваемыми числами \( 0,000001\)?).

Прочитай эту статью и все поймешь!

Но всегда ли все так легко? Где на числовой оси мы отметим \( \sqrt<6>\), \( \left( 4-\sqrt <3>\right)\), \( \frac<\sqrt[6]<6>><\sqrt<13>+\frac<4><13>>\).

Как их сравнить, например, с числом \( 5\)? Вот в этом-то и загвоздка … )

Для начала поговорим в общих чертах как и что сравнивать.

Если надо сравнить числа \( a\) и \( b\), между ними ставим знак \( \vee \) (происходит от латинского слова Versus или сокращенно vs. – против): \( a\vee b\).

Этот знак заменяет неизвестный нам знак неравенства (\( >\text

5 вариантов сравнения дробей

Например, нам необходимо сравнить две дроби: \( 1,6\) и \( 1\frac<6><13>\).

Давай разберем каждый вариант

Вариант 1. Сравнение дробей с помощью приведения к общему знаменателю

Запишем \( 1,6\) в виде обыкновенной дроби:

\( 1,6=1\frac<6><10>=1\frac<3><5>\) — (как ты видишь, я также сократила на \( 2\) числитель и знаменатель).

Теперь нам необходимо сравнить дроби:

Сейчас мы можем продолжить сравнивать также двумя способами. Мы можем:

Способ 1. Числитель больше знаменателя

Просто приведите все к общему знаменателю, представив обе дроби как неправильные (числитель больше знаменателя):

Какое число больше? Правильно, то, у которого числитель больше, то есть первое.

Способ 2. Отбросьте единицу

«Отбросьте» \( 1\) (считай, что мы из каждой дроби вычли единицу, и соотношение дробей друг с другом, соответственно, не изменилось) и будем сравнивать дроби:

Приводим их также к общему знаменателю:

Заметь, в принципе мы можем не считать знаменатель. Мы итак видим, что он одинаков и нам необходимо сравнивать числитель. Тогда зачем мы будем тратить время на подсчет знаменателя?

Мы получили абсолютно точно такой же результат, как и в предыдущем случае – первое число больше, чем второе:

Проверим также, правомерно ли мы вычли единицу? Посчитаем разницу в числителе при первом расчете и втором:

1) \( 104-95=9\)

2) \( 39-30=9\)

Итак, мы рассмотрели, как сравнивать дроби, приводя их к общему знаменателю. Перейдем к другому методу – сравнение дробей приводя их к общему… числителю.

Вариант 2. Сравнение дробей с помощью приведения к общему числителю

Да, да. Это не опечатка. В школе редко кому рассказывают этот метод, но очень часто он весьма удобен. Чтобы ты быстро понял его суть, задам тебе только один вопрос – «в каких случаях значение дроби наибольшее?»

Конечно, ты скажешь «когда числитель максимально большой, а знаменатель максимально маленький».

Например, ты же точно скажешь, что \( \frac<8> <13>\frac<6><28>\).

Как ты видишь, знаменатели здесь разные, а вот числители одинаковы. Однако, для того, чтобы сравнить эти две дроби, тебе не обязательно искать общий знаменатель. Хотя… найди его и посмотри, вдруг знак сравнения все же неправильный?

Вернемся к нашему изначальному заданию – сравнить \( 1\frac<3><5>\)и \( 1\frac<6><13>\). Будем сравнивать \( \frac<3><5>\) и \( \frac<6><13>\).

Приведем данные дроби не к общему знаменателю, а к общему числителю.

Для этого просто числитель и знаменатель первой дроби умножим на \( 2\). Получим:

Какая дробь больше? Правильно, первая.

Вариант 3. Сравнение дробей с помощью вычитания

Как сравнивать дроби с помощью вычитания? Да очень просто.

Мы из одной дроби вычитаем другую. Если результат получается положительным, то первая дробь (уменьшаемое) больше второй (вычитаемое), а если отрицательным, то наоборот.

В нашем случае попробуем из второй вычесть первую дробь: \( 1\frac<6><13>-1,6\).

Наше выражение приобретает вид:

Далее нам все равно придется прибегнуть к приведению к общему знаменателю.

Вопрос как: первым способом, преобразуя дроби в неправильные, или вторым, как бы «убирая» единицу? Кстати, это действие имеет вполне математическое обоснование. Смотри:

Мне больше нравится второй вариант, так как перемножение в числителе при приведении к общему знаменателю становится в разы проще.

Приводим к общему знаменателю:

Здесь главное не запутаться, какое число и откуда мы отнимали. Внимательно посмотреть ход решения и случайно не перепутать знаки. Мы отнимали от второго числа первое и получили отрицательный ответ, значит.

Правильно, первое число больше второго.

Вариант 4. Сравнение дробей с помощью приведения к виду десятичной дроби

Разобрался в предыдущем примере? А теперь попробуй сравнить дроби:

Стоп, стоп. Не спеши приводить к общему знаменателю или вычитать.

Посмотри: \( 1\frac<3><5>\) можно легко перевести в десятичную дробь. Сколько это будет? Правильно. Что в итоге больше?

Сравним ответы:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Сравнение степеней

Теперь представим, что нам необходимо сравнить не просто числа, а выражения, где существует степень (читай раздел про степени).

Конечно, ты без труда поставишь знак:

\( <<2>^<4>>

Раскроем скобки и сравним то, что получится:

Введем некоторое натуральное число \( k\), как разницу между \( m\) и \( n\).

Логично, неправда ли?

А теперь еще раз обратим внимание на условие — \( 0

Как ты понял, мы рассмотрели случай, когда основания степеней равны.

Теперь посмотрим, когда основание находится в промежутке от \( 0\) до \( 1\), но равны показатели степени. Здесь все очень просто.

Запомним, как это сравнивать на примере:

Конечно, ты быстро посчитал:

Поэтому, когда тебе будут попадаться похожие задачи для сравнения, держи в голове какой-нибудь простой аналогичный пример, который ты можешь быстро просчитать, и на основе этого примера проставляй знаки в более сложном.

Выполняя преобразования, помни, что если ты домножаешь, складываешь, вычитаешь или делишь, то все действия необходимо делать и с левой и с правой частью (если ты умножаешь на \( 2\), то умножать необходимо и то, и другое).

Кроме этого, бывают случаи, когда делать какие-либо манипуляции просто невыгодно. Например, тебе нужно сравнить \( <<5>^<2>>\vee <<4>^<3>>\). В данном случае, не так сложно возвести в степень, и расставить знак исходя из этого:

Источник

Степень с натуральным показателем

Что такое степень?

Степенью называют произведение из нескольких одинаковых множителей. Например:

Значение данного выражения равно 8

Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:

Это выражение читается так: « два в третьей степени равно восемь» или « третья степень числа 2 равна 8».

Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.

А число, которое надписано над числом 5 называют показателем степени. В выражении 5 3 показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза

Саму операцию перемножения одинаковых множителей называют возведением в степень.

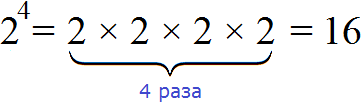
Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:

Видим, что число 2 в четвёртой степени есть число 16.

Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.

Вообще, определение степени с натуральным показателем выглядит следующим образом:

Примеры:

Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.

Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25

Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2

Получилась ошибка, поскольку число 5 во второй степени не равно 10.

Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:

Например, число 5 в первой степени есть само число 5

Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.

Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1

А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:

А выражение 0 0 не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 0 0 может иметь смысл.

Для тренировки решим несколько примеров на возведение чисел в степени.

Пример 1. Возвести число 3 во вторую степень.

Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3

Пример 2. Возвести число 2 в четвертую степень.

Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2

2 4 =2 × 2 × 2 × 2 = 16

Пример 3. Возвести число 2 в третью степень.

Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2

Возведение в степень числа 10

Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.

Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2

Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени

Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10

Пример 2. Возведём число 10 в третью степень.

В данном случае после единицы будут стоять три нуля:

Пример 3. Возведем число 10 в четвёртую степень.

В данном случае после единицы будут стоять четыре нуля:

Пример 4. Возведем число 10 в первую степень.

В данном случае после единицы будет стоять один нуль:

Представление чисел 10, 100, 1000 в виде степени с основанием 10

Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.

Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 10 1

Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10 2

Пример 3. Представим число 1 000 в виде степени с основанием 10.

Пример 4. Представим число 10 000 в виде степени с основанием 10.

Возведение в степень отрицательного числа

При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.

Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)

Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.

Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.

В случае с выражением −2 2 происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.

Поэтому выражение −2 2 вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2

Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4

Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2) 2 сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.

Пример 2. Возвести число −2 в третью степень.

Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)

Пример 3. Возвести число −2 в четвёртую степень.

Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)

(−2) 4 = (−2) × (−2) × (−2) × (−2) = 16

Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.

Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3

В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.

Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.

Пример 7. Возвести число −5 в третью степень.

Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:

Пример 8. Возвести число −4 в четвёртую степень.

Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:

(−4) 4 = (−4) × (−4) × (−4) × (−4) = 256

Нахождение значений выражений

При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.

Пример 1. Найти значение выражения 2 + 5 2

Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2

Пример 10. Найти значение выражения −6 2 × (−12)

Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:

Завершаем пример, умножив −36 на (−12)

−6 2 × (−12) = −36 × (−12) = 432

Пример 11. Найти значение выражения −3 × 2 2

Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3

Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.

Пример 12. Найти значение выражения (3 2 + 1 × 3) − 15 + 5

(3 2 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2

Пример 13. Найти значение выражения 2 × 5 3 + 5 × 2 3

Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:

2 × 5 3 + 5 × 2 3 = 2 × 125 + 5 × 8 = 250 + 40 = 290

Тождественные преобразования степеней

Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.

(2 3 ) 2 это произведение двух степеней, каждая из которых равна 2 3

При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2

Этот пример можно значительно упростить. Для этого показатели выражения (2 3 ) 2 можно перемножить и записать это произведение над основанием 2

После перемножения показателей, получится другая степень, значение которой можно найти.

Пример 2. Найти значение выражения (3 2 ) 2

В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:

Рассмотрим остальные преобразования.

Умножение степеней

Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.

2 2 × 3 3 = 4 × 27 = 108

В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.

Например, умножим 2 2 на 2 3

Вообще, для любого a и показателей m и n выполняется следующее равенство:

Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.

В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.

Пример 1. Представить в виде степени выражение 5 8 × 25

В данной задаче нужно сделать так, чтобы вместо выражения 5 8 × 25 получилась одна степень.

В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:

Запишем решение покороче:

Пример 2. Представить в виде степени выражение 2 9 × 32

Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?

Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 3 1 и 3 1

Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:

Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9

Далее вычисляем значение каждой степени и находим произведение:

Пример 5. Выполнить умножение x × x

Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:

Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.

Решение данного примера желательно записать так:

Пример 6. Выполнить умножение x 2 × x

Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

Пример 7. Выполнить умножение y 3 y 2 y

Показатель третьего сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

Пример 8. Выполнить умножение aa 3 a 2 a 5

Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

Пример 9. Представить степень 3 8 в виде произведения степеней с одинаковыми основаниями.

Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.

Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:

Возведение в степень произведения

Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.

Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:

Принцип работы данного правила основан на определении степени, которое было дано в самом начале.

Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:

От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:

Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:

Пример 2. Найти значение выражения (2 × 3 × 4) 2

Пример 3. Возвести в третью степень произведение a × b × c

Заключим в скобки данное произведение, и в качестве показателя укажем число 3

Далее возводим в третью степень каждый множитель данного произведения:

Пример 4. Возвести в третью степень произведение 3xyz

Заключим в скобки данное произведение, и в качестве показателя укажем 3

Возведём в третью степень каждый множитель данного произведения:

В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.

5 2 × 3 2 = 25 × 9 = 225

5 2 × 3 2 = (5 × 3) 2 = (15) 2 = 225

Возведение степени в степень

Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.

При возведении степени в степень основание оставляют без изменений, а показатели перемножают:

К примеру, выражение (2 3 ) 2 является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:

(2 3 ) 2 = 2 3 × 2 = 2 6

(2 3 ) 2 = 2 3 × 2 = 2 6 = 64

Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.

А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:

(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2

Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:

(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6

(2 × 2 × 2) 2 = 2 2 × 2 2 × 2 2 = 2 2 + 2 + 2 = 2 6 = 64

В степень также может возводиться произведение, сомножители которого тоже являются степенями.

(2 2 × 3 2 ) 3 = 2 2×3 × 3 2×3 = 2 6 × 3 6 = 64 × 729 = 46656

Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.

Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:

Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:

Пример 2. Найти значение выражения (3 3 ) 2

Основание оставляем без изменений, а показатели перемножаем:

Пример 3. Выполнить возведение в степень в выражении (xy)³

Возведём в третью степень каждый множитель произведения:

Пример 4. Выполнить возведение в степень в выражении (abc)⁵

Возведём в пятую степень каждый множитель произведения:

Пример 5. Выполнить возведение в степень в выражении (−2ax) 3

Возведём в третью степень каждый множитель произведения:

Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.

Пример 6. Выполнить возведение в степень в выражении (10xy) 2

Пример 7. Выполнить возведение в степень в выражении (−5x) 3

Пример 8. Выполнить возведение в степень в выражении (−3y) 4

Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴

Пример 10. Упростите выражение x 5 × (x 2 ) 3

Степень x 5 пока оставим без изменений, а в выражении (x 2 ) 3 выполним возведение степени в степени:

Основное свойство степени можно использовать в случае, если основания исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.

Запишем решение данного примера:

Деление степеней

Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.

Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.

Например, найдем значение выражения 2 3 : 2 2

Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.

Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.

Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:

Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.

При решении примера 2 2 : 2 2 также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 2 2 и 2 2 равна нулю:

В математике принято считать, что любое число в нулевой степени есть единица:

Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 2 2 : 2 2 обычным методом, не используя правило деления степеней, получится единица.

Пример 2. Найти значение выражения 4 12 : 4 10

Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

4 12 : 4 10 = 4 12 − 10 = 4 2 = 16

Пример 3. Представить частное x 3 : x в виде степени с основанием x

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:

Пример 4. Представить частное x 3 : x 2 в виде степени с основанием x

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:

Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:

Пример 5. Выполнить деление x 12 : x 3

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Пример 6. Найти значение выражения

В числителе выполним умножение степеней с одинаковыми основаниями:

Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Завершаем пример, вычислив степень 7 2

Пример 7. Найти значение выражения

Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (2 3 ) 4

Теперь выполним в числителе умножение степеней с одинаковыми основаниями:

Теперь применяем правило деления степеней с одинаковыми основаниями:

Значит, значение выражения 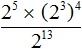равно 16

В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.

В числителе выполним возведение степени в степень. Сделать это нужно с выражением (2 2 ) 3

Пример 8. Найти значение выражения

Теперь можно применить правило деления степеней:

Возведение в степень обыкновенных дробей

Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.

Например, возведём обыкновенную дробь во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2

Итак, чтобы вычислить значение выражения 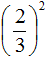, нужно возвести во вторую степень числитель и знаменатель данной дроби:

Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности

Значит обыкновенная дробь во второй степени равна дроби .

Приведённое правило работает следующим образом. Дробь во второй степень это произведение двух дробей, каждая из которых равна

Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:

А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 2 2 и 3 2 соответственно:

Откуда и получится ответ .

Вообще, для любого a и b ≠ 0 выполняется следующее равенство:

Это тождественное преобразование называют возведением в степень обыкновенной дроби.

Пример 2. Возвести дробь в третью степень

Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:

Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.

Например, возведём дробь во вторую степень:

Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:

Ответ положителен по причине того, что выражение 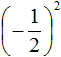представляет собой произведение двух сомножителей, каждый из которых равен дроби

А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:

Если возводить дробь в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:

Здесь ответ отрицателем по причине того, что выражение 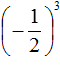представляет собой произведение трёх множителей, каждый из которых равен дроби

Сначала перемножили и , получили , но затем умножив на мы получим отрицательный ответ

Пример 3. Найти значение выражения

Выполним возведение в степень обыкновенной дроби:

Далее вычислим значение получившегося выражения:

Возведение в степень десятичных дробей

При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5

Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:

Пример 2. Найти значение степени (−1,5) 3

Показатель степени является нечётным числом. Значит ответ будет отрицательным

Пример 3. Найти значение степени (−2,4) 2

Показатель степени является чётным числом. Значит ответ будет положительным:

Источник