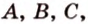Что такое стереометрические фигуры

Стереометрия

Что такое стереометрия

Стереометрия — раздел евклидовой геометрии, в котором изучаются свойства фигур в пространстве.

Если основными фигурами планиметрии являются точка и прямая, то в стереометрии к изучению добавляется плоскость.

Примеры стереометрических фигур:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Нередко основным способом решения задач в стереометрии является рассмотрение разнообразных плоскостей при выполнении планиметрических законов.

В стереометрии используются следующие обозначения:

Базовые теоремы, аксиомы и определения стереометрии

Сечения многогранников

При решении задач по стереометрии нередко придется строить сечения многогранников на определенной плоскости. Далее приведены базовые определения, которые относятся к сечению.

Секущей плоскость будет называться в случае, если по обе стороны от нее будут находиться точки пирамиды, куба, параллелепипеда или же призмы.

Сечением пирамиды, куба, параллелепипеда или же призмы будет являться фигура, которая состоит из всех точек, являющихся общими фигуры и секущей плоскости.

Секущая плоскость будет пересекать грани пирамиды, куба, параллелепипеда или же призмы по отрезкам, исходя из этого, сечение является многоугольником, который лежит в секущей плоскости, со сторонами — указанными отрезками.

Чтобы построить сечение указанных выше фигур стереометрии, необходимо построение точек пересечения секущей плоскости и ребер фигуры, а после соединяться каждые две из них, которые лежат в одной грани.

Симметрия фигур

Взаимное расположение прямых в пространстве

В пространстве прямые лежат либо в одной плоскости, либо в разных плоскостях.

Расстояние между фигурами

Основные теоремы стереометрии

Теоремы о параллельности прямых и плоскостей

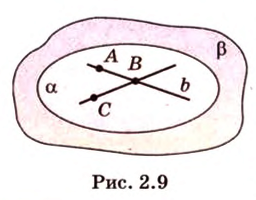
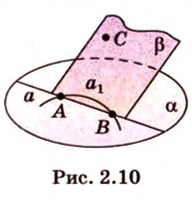
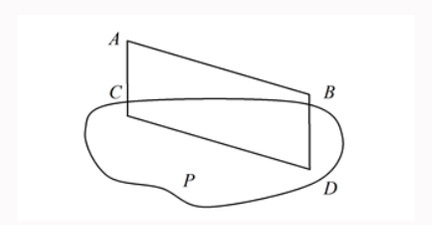
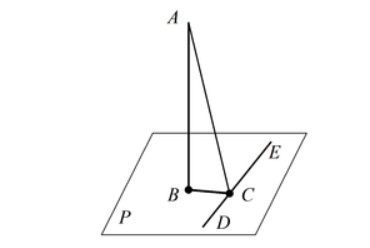
Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.

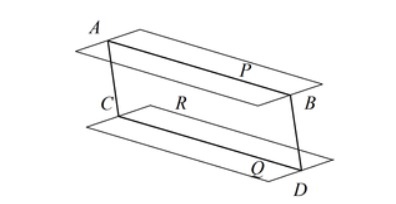
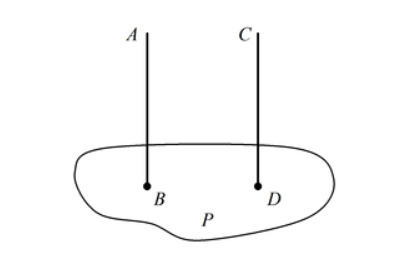
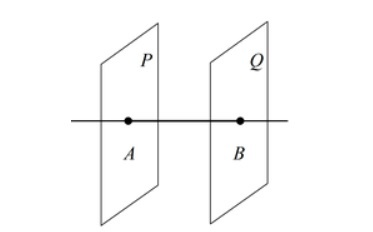
Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.

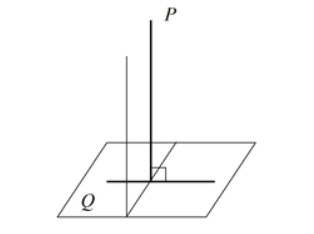
Теоремы о перпендикулярности прямых и плоскостей

Теоремы о перпендикулярности плоскостей

Теорема о скрещивающихся прямых

Основные аксиомы стереометрии

Рассмотрим четыре основные аксиомы стереометрии.

Источник

61. Стереометрия Читать 0 мин.

61.26. Основные стереометрические фигуры

Среди огромного множества объемных фигур можно выделить три большие группы:

ПРИЗМЫ:

Примеры:

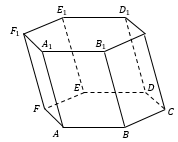
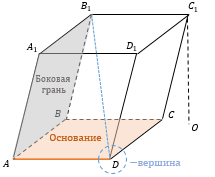
Элементы призмы:

Два n − угольника являются основаниями призмы (ABCD), параллелограммы − боковыми гранями (AB B₁A₁).

Стороны граней называются ребрами призмы (например, AD), а концы ребер − вершинами призмы (например, D).

Виды призм:

Прямая призма –

призма, боковые ребра которой перпендикулярны плоскостям оснований.

Наклонная призма –

призма, боковые ребра которой являются наклонными к плоскостям оснований.

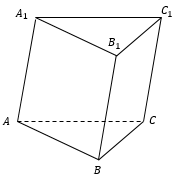
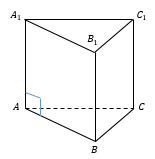
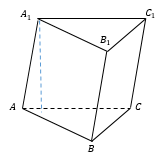
$ABCA_1B_1C_1$– прямая треугольная призма

$ABCA_1B_1C_1$– наклонная треугольная призма

Свойства призмы:

Для прямой призмы высотой будет является любое из боковых ребер.

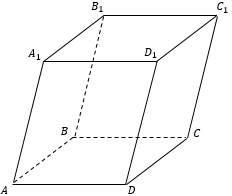
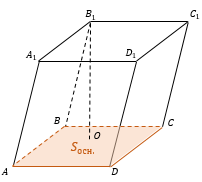
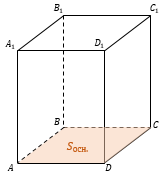
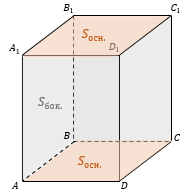
$ABCDA_1B_1C_1D_1$ — произвольная призма.

$ABCDA_1B_1C_1D_1$ — прямая призма.

Площадь боковой поверхности прямой призмы:

где P — периметр перпендикулярного сечения, h — высота. То есть:

Особенные призмы:

Все грани – прямоугольники.

Все грани − квадраты.

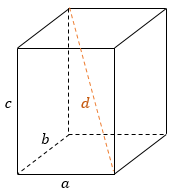
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:

где a, b, c − длины ребер, выходящих из одной вершины, d − диагональ параллелепипеда.

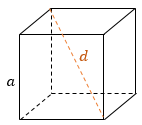
Квадрат диагонали куба равен квадрату его ребра, умноженному на 3:

где a − длина ребра куба.

Площадь поверхности куба можно найти по формуле:

Объем прямоугольного параллелепипеда находят по формуле

Объем куба можно найти по формуле:

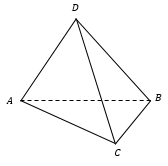
ПИРАМИДЫ:

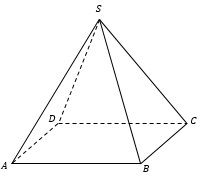
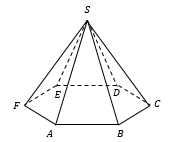
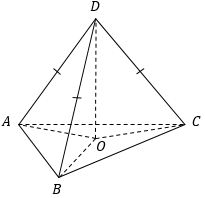
n-угольная пирамида – многогранник, одна грань которого – n-угольник, а остальные грани − треугольники с общей вершиной.

Примеры:

Элементы пирамиды:

n-угольник называется основанием пирамиды (ABCD), а треугольники − боковыми гранями (например, SBC).

Особенные пирамиды:

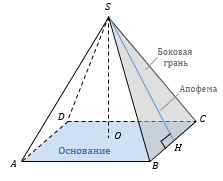
Правильная пирамида – пирамида, основанием которой является правильный многоугольник, а высота опускается в центр вписанной и описанной окружности многоугольника, лежащего в основании пирамиды. В правильной пирамиде обязательно равны между собой ребра основания, и равны между собой боковые ребра. Но не обязательно боковое ребро равно ребру в основании.

Усеченная пирамида – многогранник, вершинами которого служат вершины основания пирамиды и вершины её сечения плоскостью, параллельной основанию пирамиды. Основания усеченной пирамиды − подобные многоугольники.

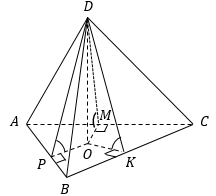
Свойства пирамиды:

О – центр вписанной окружности

О – центр описанной окружности

Площадь боковой поверхности правильной пирамиды можно найти по одной формуле

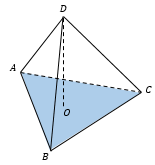
Если ABCD — произвольная пирамида, то

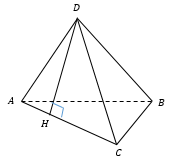
Если ABCD — правильная пирамида, то

ТЕЛА ВРАЩЕНИЯ:

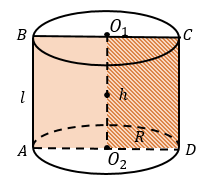
Цилиндр – фигура, полученная в результате вращения прямоугольника вокруг одной из его сторон.

Элементы цилиндра:

l (AB, CD) – образующая

Свойства цилиндра:

Любое сечение цилиндра, параллельное его основанию – круг, равный основанию цилиндра.

Сечение цилиндра, наклонное к его оси и основанию – эллипс.

Боковая поверхность равна:

где R − радиус основания, h − высота, l − образующая цилиндра.

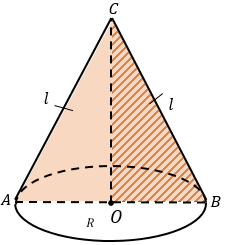
Конус – фигура, полученная в результате вращения прямоугольного треугольника вокруг одного из катетов.

Элементы конуса:

OС − ось вращения и высота

ABC − осевое сечение конуса, полученного вращением треугольника ABC вокруг его стороны OС

Свойства конуса:

Любое сечение конуса, параллельное его основанию – круг, подобный основанию конуса.

Сечение конуса, наклонное к его основанию и не проходящее через вершину – эллипс.

Боковая поверхность равна:

где R − радиус основания, l − образующая конуса.

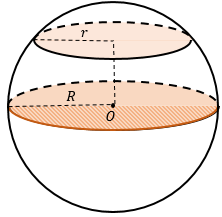
Сфера – фигура, полученная в результате вращения полуокружности вокруг ее диаметра.

Шар – фигура, полученная вращением полукруга вокруг его диаметра.

Свойства шара и сферы:

Сечение шара плоскостью, проходящей через его центр, называется большим кругом (круг радиуса R).

Источник

Содержание:

Стереометрия:

Что такое стереометрия

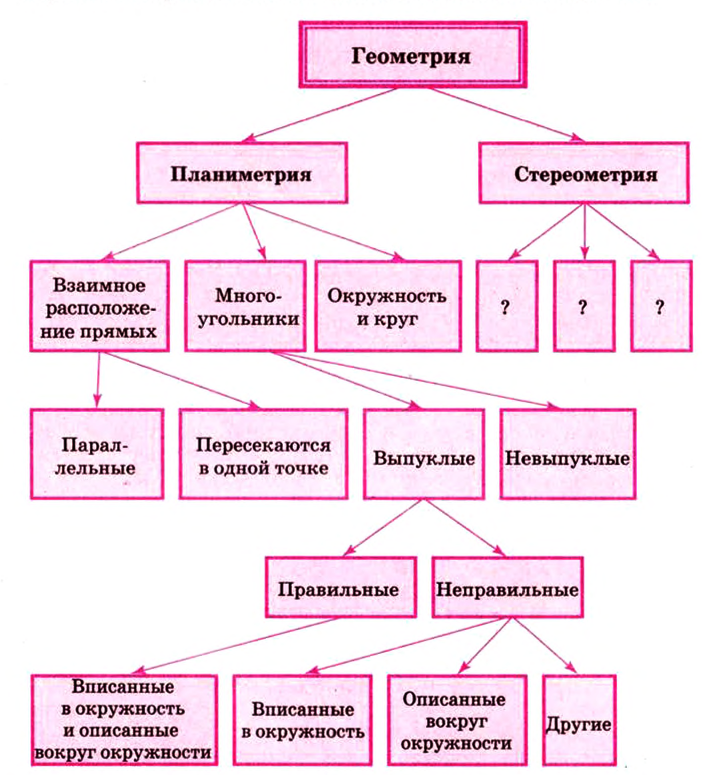
Схематически это выглядит так:

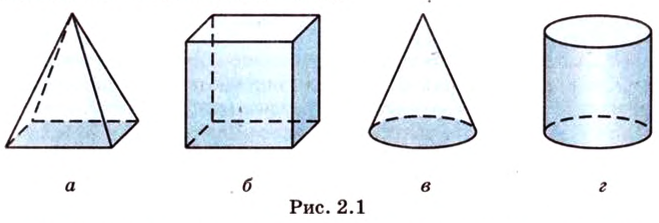
Фигуры, которые изучаются в стереометрии, называются геометрическими или пространственными. На рисунке 2.1 изображены некоторые пространственные фигуры: пирамида, параллелепипед, конус, цилиндр.

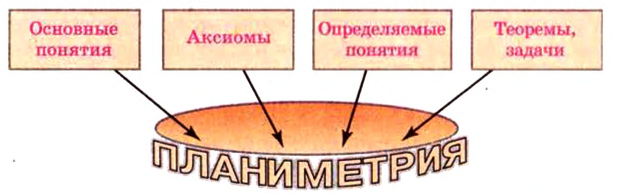
Напомним структуру логического построения планиметрии:

В стереометрии рассматривают более одной плоскости. Пространство состоит из бесконечного количества плоскостей, прямых и точек. Поэтому все аксиомы планиметрии имеют место и в стереометрии. Однако при этом некоторые из них приобретают другой смысл. Так, аксиома I, в планиметрии утверждает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Именно в таком понимании эта аксиома применялась в процессе построения геометрии на плоскости. Теперь эта аксиома утверждает вообще существование точек, не лежащих на данной прямой, в пространстве. Из нее непосредственно не вытекает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Это требует уже специального доказательства.

Аксиомы стереометрии

Формулирование некоторых аксиом планиметрии как аксиом стереометрии требует уточнения. Это касается, например, аксиом .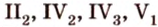

Приведем эти уточнения.

Понятно, что с увеличением количества основных фигур появляются новые аксиомы об их свойствах:

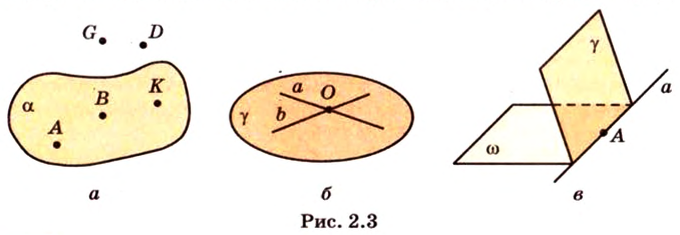
Аксиома 1 указывает на то, что любая плоскость все пространство не исчерпывает. Существуют точки пространства, которые ей не принадлежат.

Аксиома 2 утверждает, что две прямые, пересекающиеся в пространстве, всегда определяют одну плоскость. Из аксиомы 3 следует, что если две различные плоскости имеют общую точку, то они имеют множество общих точек, образующих прямую, которая содержит эту точку.

Итак, используя рисунок 2.3, аксиомы можно записать:

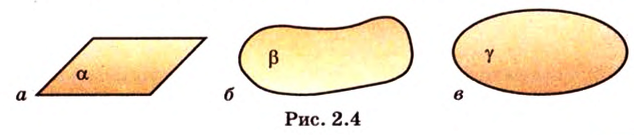
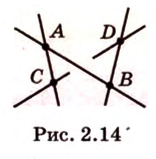
Плоскости изображают по-разному. На рисунке 2.4 показаны некоторые примеры различных изображений плоскостей.

Далее в стереометрии мы будем использовать все определяемые понятия планиметрии, дополнять их новыми, собственно стереометрическими, формулировать и доказывать свойства пространственных фигур.
Как видим, логическое построение планиметрии и стереометрии одинаково, отличаются они лишь некоторым содержанием основных понятий, аксиом, определений, теорем.

Пример №1

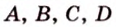
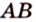
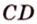
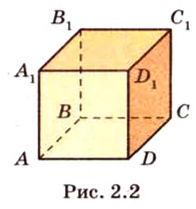
Точки не лежат на одной плоскости. Докажите, что прямые и не пересекаются.

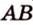
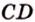
Докажем методом от противного. Допустим, что прямые и пересекаются (рис. 2.5).

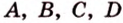
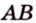
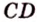
Тогда, по аксиоме II₃, через них можно провести плоскость, которой принадлежат эти прямые. Это означает, что точки также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые и не пересекаются, что и требовалось доказать.
Заметим, что школьный курс геометрии посвящен евклидовой геометрии. Несмотря на то что с течением времени геометрия Евклида была существенно дополнена и откорректирована, ее по-прежнему называют именем древнего ученого. Такое уважение вызвано широтой практического применения евклидовой геометрии. Она используется в технических науках, картографии, геодезии, астрономии и др.

Следствия из аксиом стереометрии

Проанализировав все сказанное ранее, можно утверждать, что логическое построение геометрии имеет следующий вид:

Важное место в геометрии занимают аксиомы. Они выражают наиболее существенные свойства основных геометрических фигур. Все остальные свойства геометрических фигур устанавливаются рассуждениями, опирающимися на аксиомы или ранее доказанные утверждения, которые опираются на аксиомы. Такие рассуждения называют доказательствами. Утверждение, истинность которого доказана и которое используют для доказательства других утверждений, называют теоремой. Простейшими из них являются утверждения для основных фигур стереометрии. Они называются следствиями из аксиом стереометрии. Рассмотрим теоремы, которые являются следствиями из аксиом стереометрии.

Теорема 1

Через прямую и точку, не принадлежащую ей, можно провести плоскость, и притом только одну.

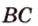
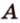
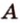
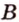
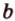
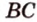
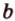
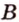
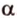
Пусть — данная прямая и — точка, не принадлежащая ей (рис. 2.9). Через точки и проведем прямую . Прямые и различны и пересекаются в точке . По аксиоме II₃ через них можно провести плоскость . Докажем, что она единственная, методом от противного.

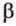
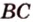
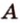
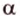
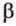
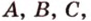
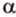
Допустим, что существует другая плоскость , которая содержит прямую и точку . Тогда, согласно аксиоме II4, плоскости и пересекаются по общей прямой, которой принадлежат точки что противоречит условию. Предположение неверно. Плоскость — единственная. Теорема доказана.

Теорема 2
Если две точки прямой принадлежат плоскости, то и вея прямая принадлежит этой плоскости.

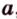
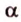
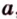
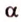
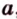
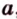
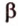
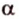
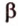
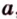
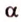
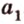
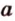
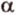
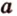
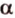
Пусть заданы прямая , плоскость и точки А и В прямой , принадлежащие (рис. 2.10). Выберем точку С, которая не принадлежит прямой . Через точку С и прямую проведем плоскость . Если и совпадут, то прямая принадлежит плоскости . Если же плоскости и различны и имеют две общие точки и , то они пересекаются по прямой , содержащей эти точки. Поэтому через две точки и проходят две прямые и , что противоречит аксиоме принадлежности I₂. Поэтому и — совпадают. Однако поскольку , принадлежит плоскости , то и прямая также принадлежит .

Теорема 3

Через три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.

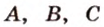
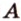
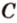
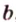
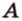
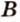
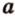
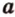
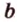
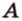
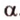
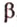
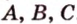
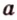
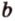
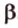
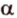
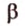
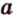
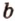
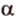
Пусть — заданные точки (рис. 2.11). Проведем через точки и прямую , а через точки и — прямую . Прямые и различны и имеют общую точку . Через них можно провести плоскость . Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость , содержащая точки . Тогда, по теореме 2, прямые и принадлежат плоскости . Поэтому плоскости и имеют две общие прямые и , которые пересекаются, что противоречит аксиоме II₃. Итак, плоскость — единственная. Теорема доказана.

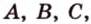
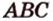
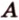
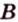
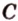
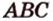
Отметим, если плоскость определена тремя точками, которые не лежат на одной прямой, например то в таком случае пользуются обозначением: (). Читается: «плоскость, заданная точками , и », или сокращенно «плоскость ».

Пример №2

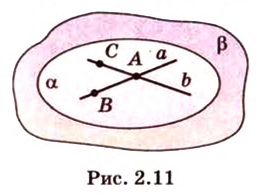
Можно ли через точку пересечения двух данных прямых провести третью прямую, которая бы не лежала с ними в одной плоскости?

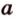
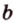
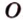
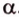
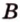
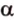
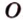
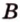
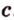
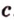
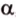
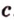
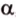
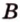
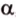
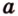
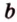
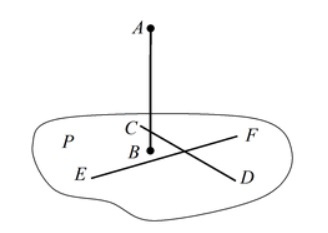
Через прямые и (рис. 2.12), которые имеют общую точку , можно провести плоскость . Возьмем точку , которая не принадлежит . Через точки и проведем прямую . Прямая не лежит на плоскости , так как если бы прямая принадлежала плоскости , то и точка принадлежала бы плоскости . Поэтому через точку пересечения прямых и можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.

Очевидно, что точки плоскости задают прямые, которые будут принадлежать этой самой плоскости. Если же взять точку пересечения двух прямых на плоскости и точку вне плоскости, то через любые две точки пространства можно провести прямую. Эта прямая будет иметь только одну общую точку с плоскостью, а значит, будет ее пересекать.

Пример №3

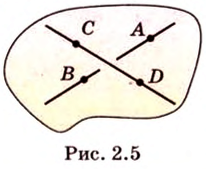
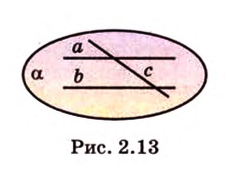
Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.

Пример №4

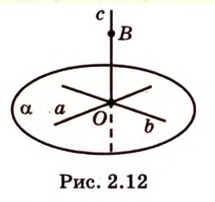
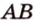
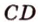
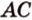
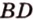
Докажите, что если прямые и не лежат в одной плоскости, то прямые и также не лежат в одной плоскости.

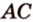
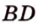
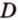
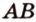
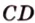
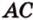
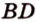
Докажем методом от противного. Допустим, что прямые и лежат в одной плоскости (рис. 2.14). Тогда точки принадлежат этой плоскости, а следовательно, прямые и принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые и не принадлежат одной плоскости, что и требовалось доказать.

Пример №5

Сколько всего существует различных плоскостей, проходящих через прямую и точку в пространстве?

Если в пространстве даны прямая и точка, лежащая на ней, то ими определяется множество плоскостей, поскольку через прямую проходит множество различных плоскостей.
Если же точка не лежит на прямой, то по следствию из аксиом стереометрии такую плоскость можно построить только одну.

Ответ. Бесконечно много или одна.

Взяв вне этой прямой произвольную точку, мы всякий раз будем иметь другую плоскость, не совпадающую с ранее построенной. Таких плоскостей множество.
Через данную точку вне прямой можно провести либо прямую, которая пересекает данную прямую, либо прямую, параллельную данной. Оба случая задают одну плоскость.

Сечения

Анализируя окружающий мир и систематизируя его предметы по форме, мы убеждаемся, что много из них «усечены» или «склеены». Разъединив их, получим поверхность, которую называют их сечением.

С сечениями мы сталкиваемся в разнообразных ситуациях: в быту, в столярничестве, токарстве и т.д. Решением задач на сечения геометрических фигур или других тел занимаются в черчении и конструкторской практике. Сечения выполняют для пространственных геометрических фигур.

Каждая плоскость разбивает пространство на два полупространства, а концы отрезка могут лежать в различных полупространствах (рис. 2.20, а) относительно некоторой плоскости, на плоскости (рис. 2.20, б) или в одном полупространстве (рис. 2.20, в).

Если ни одна из двух точек не принадлежит плоскости, а отрезок, соединяющий их, имеет с этой плоскостью общую точку, то говорят, что данные точки лежат по разные стороны относительно плоскости, или отрезок пересекает плоскость. Если же как минимум две точки пространственной геометрической фигуры лежат по разные стороны плоскости, то говорят, что плоскость эту фигуру пересекает, такую плоскость называют секущей.

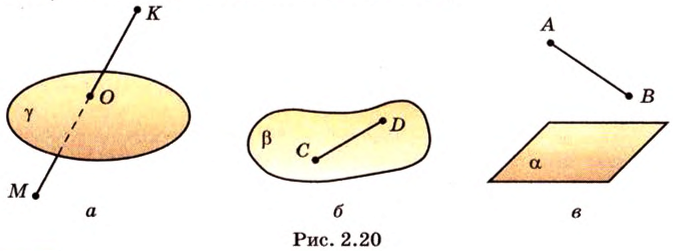
Фигура, которая состоит из всех общих точек геометрической фигуры и секущей плоскости, называется сечением геометрической фигуры. На рисунке 2.21 сечения изображены цветом.

Если плоскость грани многогранника и плоскость сечения имеют две общие точки, то они пересекаются по прямой, проходящей через эти точки. Эту прямую называют линией пересечения данных плоскостей.
Плоскость сечения многогранника имеет общие прямые с плоскостями граней многогранника. Прямую, по которой плоскость сечения пересекает плоскость любой грани многогранника, называют следом плоскости сечения. Следов столько, сколько плоскостей граней пересекает плоскость сечения.

При построении сечения следует помнить:

Рассмотрим примеры построения сечения многогранника секущей плоскостью.

Пример №6

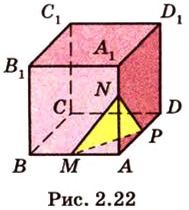
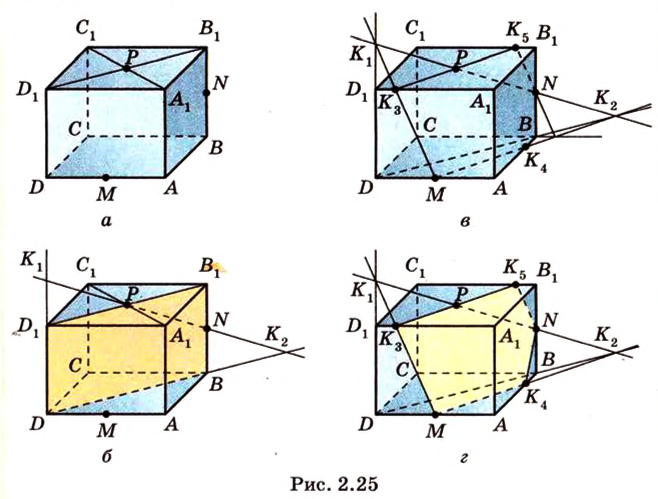
Постройте сечение куба плоскостью, проходящей через середины ребер с общей вершиной.

Построение

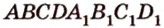
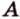
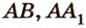
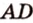
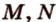
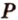
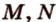
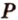
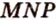
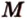
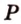
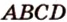
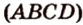
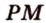
Пусть — заданный куб (рис. 2.22). Выберем одну из вершин, например , являющуюся общей для трех ребер и . Обозначим на этих ребрах точки и соответственно, являющиеся их серединами. Точки и не лежат на одной прямой, а поэтому определяют секущую плоскость (). Точки и — общие точки плоскости сечения и грани , поэтому , — сторона сечения.
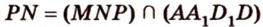
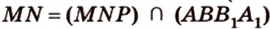
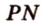
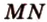
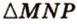
Аналогично и , поэтому и — две другие стороны сечения. Таким образом, — искомое сечение.

Пример №7

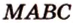
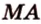
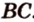
Постройте сечение пирамиды плоскостью, которая проходит через ребро и середину ребра .

Построение

Пример №8

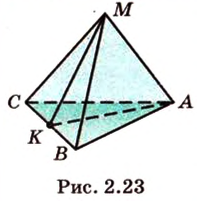
Постройте сечение пирамиды плоскостью, проходящей через три точки, которые лежат соответственно на ребрах , .

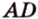
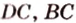
Построение

Рассмотрим случай, когда ни одна из прямых, проходящих через эти точки, не будет параллельна сторонам граней.

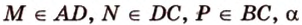
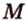
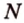
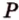
Пусть — секущая плоскость, проходящая через заданные точки , и . Построим сечение, выполняя последовательно шаги:

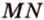
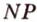
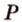
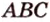
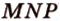
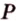
Мы нашли две стороны фигуры сечения: отрезки и (рис. 2.24, а). Точка — общая точка двух плоскостей () и (). Такие плоскости (по аксиоме II₄) пересекаются по прямой, проходящей через точку . Для построения такой прямой нужна вторая точка.

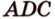
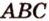
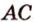
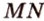
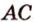
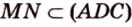
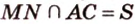
3. Плоскости () и () пересекаются по прямой . по условию не параллельна и , поэтому (рис. 2.24, б).
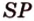
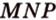
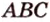
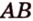
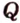
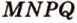
4. Прямая — линия пересечения плоскостей () и (). Пересечение этой прямой с ребром дает точку , которая является вершиной сечения. Таким образом, четырехугольник — искомое сечение (рис. 2.24, в).

Пример №9

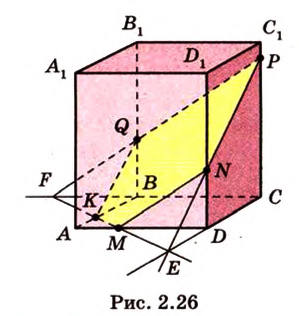
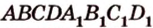
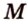
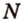
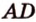
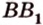
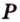
Постройте сечение прямоугольного параллелепипеда плоскостью, проходящей через середины и ребер и и точку пересечения диагоналей грани (рис. 2.25, а).

Построение

Обозначим секущую плоскость 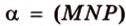. Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.

Таким образом, пятиугольник 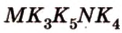— искомое сечение (рис. 2.25, г).
Приведем краткие описания построения сечения куба плоскостью, проходящей через три точки.

Пример №10

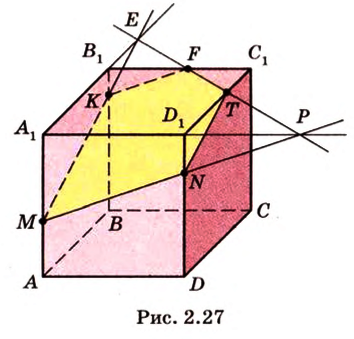
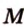
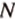
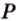
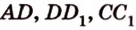
Постройте сечение куба плоскостью, проходящей через точки , , , которые принадлежат соответственно ребрам .

Построение

Секущая плоскость 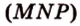) (рис. 2.26).

Пример №11

Постройте сечение куба плоскостью, проходящей через точки К, М, Т, которые принадлежат соответственно ребрам , .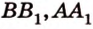

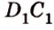
Секущая плоскость 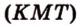(рис. 2.27).

Пример №12

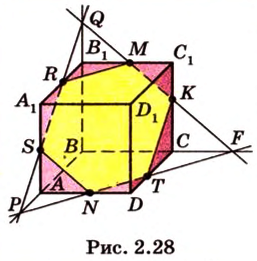
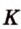
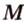
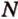
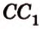
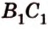
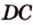
Постройте сечение куба плоскостью, проходящей через точки , , , которые принадлежат соответственно ребрам ,, .

Построение

Секущая плоскость 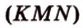(рис. 2.28).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник