Что такое сторона в математике
Что такое сторона в математике
Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, то есть два луча с общим началом называются углом. Лучи, образующие угол, называются сторонами угла, а их общее начало — вершиной угла.
Обозначение углов
Угол обозначается или одной буквой или цифрой, поставленной при вершине угла, например угол A или угол 1, или тремя буквами, из которых одна стоит при его вершине, а две другие при каких-либо точках его сторон. При обозначении угла тремя буквами, буква, стоящая при его вершине, произносится и пишется между двумя другими, например угол AOB. Слово угол в записи заменяют знаком ∠, например ∠1.
Внутренняя и внешняя область
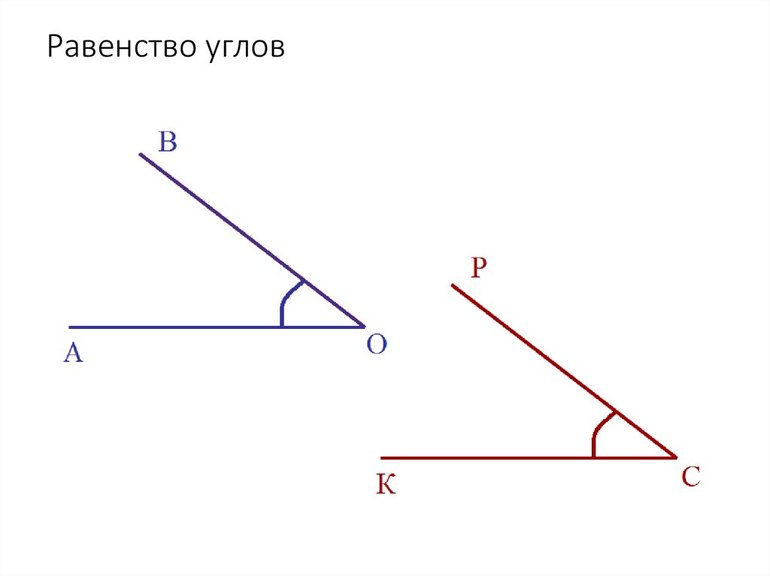
Два луча, исходящие из одной точки, образуют два угла. Для обозначения нужного угла, угол обычно помечается дугой:
Если рассматриваются оба угла, образованные двумя лучами, то они помечаются разным числом дуг, но только в том случае, если углы не равны. Равные углы обозначаются одинаково.
Любой угол делит плоскость на две области. Одна область обычно называется внутренней, а другая внешней. Внутренняя область угла — это часть плоскости, расположенная между сторонами рассматриваемого угла:
Внешняя область угла — это часть плоскости, которая не принадлежит рассматриваемому углу.
Сторона
Смотреть что такое «Сторона» в других словарях:
сторона — сущ., ж., употр. наиб. часто Морфология: (нет) чего? стороны, чему? стороне, (вижу) что? сторону, чем? стороной, о чём? о стороне; мн. что? стороны, (нет) чего? сторон, чему? сторонам, (вижу) что? стороны, чем? сторонами, о чём? о сторонах … … Толковый словарь Дмитриева
СТОРОНА — стороны, вин. сторону (сторону обл.), мн. стороны, сторон, сторонам, жен. 1. Направление; пространство или местность, расположенные в каком н. направлении от чего н. В стороне леса. Пошли в сторону леса. Пойти в разные стороны. Ветер с восточной… … Толковый словарь Ушакова
СТОРОНА — жен. вообще: направленье; | часть целого, пространство и местность вне чего либо, внешнее, наружное, от нутра или от средины удаленное; | бок, край, грань, либо одна из наружных поверхностей, плоскостей предмета; | край, область, местность,… … Толковый словарь Даля
сторона — Бок, грань, край, рука, фланг. Иди по правой руке. См. качество, область, страна бросаться во все стороны, быть на чьей либо стороне, взять чью либо сторону, в сторону, дело сторона, держать чью либо сторону, задняя сторона, лицевая сторона, ни… … Словарь синонимов
Сторона — Сторона: Сторона многоугольника отрезок, соединяющий две его соседние вершины. Сторона обязательства Сторона международного договора Воюющие стороны Стороны света Стороны монеты: аверс и реверс Стороны кассеты: «А» и «Б» Используется в названиях… … Википедия
Сторона От — Альбом Ольга Арефьева Ковчег Дата выпуска 1998 Записан 1998 Жанр Регги Длительность 120 минут … Википедия
сторона — сторона болючая ісцец; той, хто пацярпеў; сторона ображеная ісцец, жалобнік; сторона отпорная назва адказчыка пры разглядзе судовай справы; сторона поводовая ініцыятар судовага разбору справы; сторона позваная адказчык у судовым працэсе … Старабеларускі лексікон
сторона — сторона, стороны, стороны, сторон, стороне, сторонам, сторону, стороны, стороной, стороною, сторонами, стороне, сторонах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
сторона — укр., блр. сторона, др. русск. сторона, ст. слав. страна χώρα, περίχωρος (Остром., Супр.), болг. страна, сербохорв. страна, вин. стра̑ну, словен. strana, чеш., слвц. strana, польск. strona, в. луж., н. луж. strona, полаб. starna. Праслав. *storna … Этимологический словарь русского языка Макса Фасмера
СТОРОНА — СТОРОНА, ы, вин. сторону, мн. стороны, сторон, сторонам, жен. 1. Направление, а также пространство, место, расположенное в каком н. направлении от кого чего н. Подъехать с левой стороны. Две стороны. Обе стороны и стороны. Отпустить на все четыре … Толковый словарь Ожегова
Многоугольники
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :
В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.
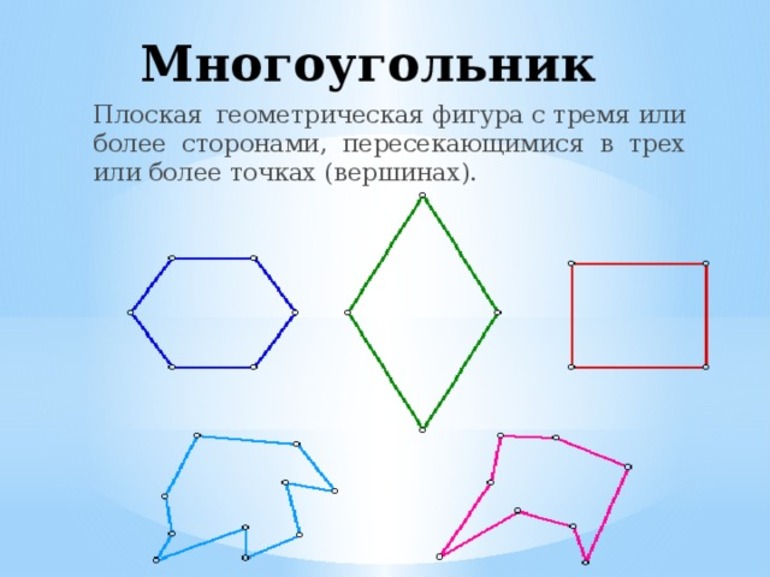
Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника ABCDE равен:
Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.
Многоугольник с тремя сторонами
Прежде чем рассматривать задачу о том, как проверить, существует ли треугольник, следует подробно изучить эту фигуру. Согласно общепринятому определению, любой замкнутый многоугольник на плоскости, который состоит из трех отрезков, пересекающихся своими концами друг с другом, является треугольником. Эта фигура имеет две группы образующих ее элементов:
Сторонами являются три отрезка, длины которых могут быть либо известны по условию задачи, либо их предстоит рассчитать. Касательно вершин следует сказать, что у любого рассматриваемого многоугольника их три. Каждую принято обозначать одной латинской буквой, например, A, B, C и так далее. Поскольку два отрезка пересекаются в вершине, то они образуют некоторый угол. Их у фигуры три, поэтому становится понятным, откуда происходит название «треугольник».
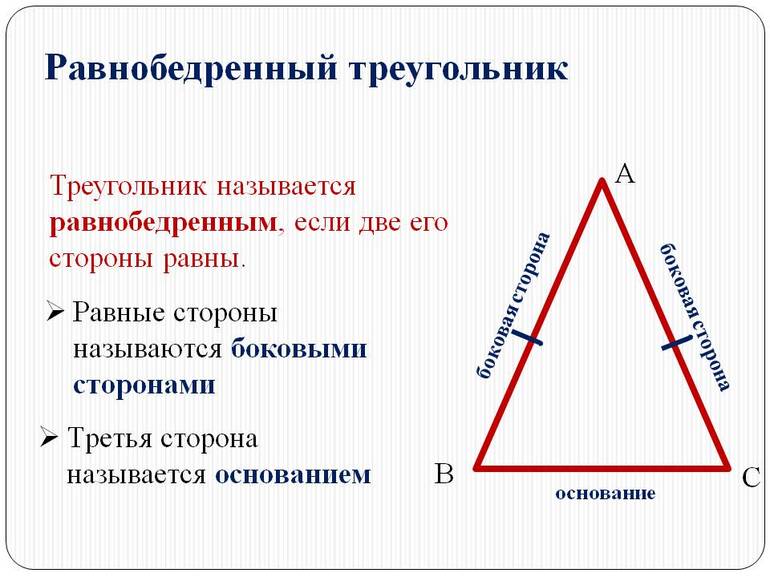
Типы фигуры
Их классификация является достаточно развитой. В ее основу положены принципы взаимоотношения длин сторон друг с другом, а также численные значения углов. В общем случае в геометрии рассматривают следующие типы треугольников:
Два основных свойства
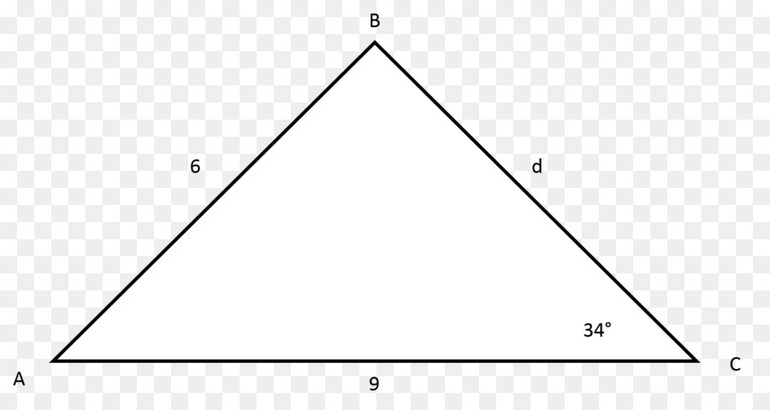
В некоторых геометрических задачах можно встретить проблемы, которые формулируются так: можно ли построить треугольник со сторонами a, b, c, если известны их длины. Либо другой тип задач, которые предполагают знание некоторых сторон и углов, и требуют определить возможность существования такой фигуры.
Ответ на все эти проблемы заключается всего в одном слове: либо «да» и такой треугольник действительно существует, либо «нет» и из заданных элементов его построить не представляется возможным. Разобраться со всеми этими задачами поможет знание двух главных свойств, которые всегда справедливы для треугольников любых типов:
Оба свойства с успехом можно и необходимо применять, чтобы проверить или узнать возможность существования того или иного треугольника. Важно понимать, что невыполнение любого из свойств говорит о невозможности построения рассматриваемой фигуры.
Вопрос вырождения
В свете изучения возможности существования треугольников важно рассмотреть вопрос их вырождения. В математике придумали универсальную формулу, которая позволяет оценить качество треугольника. Она имеет вид:
Каждый из трех множителей числителя является положительным числом, что следует из главного свойства треугольников. Величина качества CT является положительной и лежит в пределах значений 0 и 1. Возможны следующие случаи:
Теорема косинусов
Чтобы решать задачи на треугольники, недостаточно знать лишь главные их свойства. Последние позволяют лишь дать качественный, но не количественный ответ. Теорем и формул для рассматриваемых многоугольников известно много (синусов, Пифагора, медиан, Герона и др.). Однако, теорема косинусов является одной из основополагающих, поскольку позволяет по двум сторонам и углу определить значение длины третьей стороны (справедливости ради следует отметить, что теорема синусов является не менее важной, поскольку она по двум углам и стороне позволяет вычислить неизвестные стороны).
Соответствующее выражение имеет следующий вид:
c 2 = a 2 + b 2 — 2*a*b*cos (α).
Решение задач
Для закрепления полученных знаний полезно привести пару примеров решения типичных геометрических задач с треугольниками, в которых нужно будет либо дать качественный ответ, либо получить некоторое количественное значение.
Первая задача требует получить качественный ответ. Пусть имеется треугольник со сторонами 1, 2, 4. Существует ли такая фигура, требуется выяснить.
Для решения этой проблемы абсолютно неважно измеряются стороны в метрах, в сантиметрах, в дюймах или в других величинах. Важно лишь взаимоотношение между ними. Для каждой из длин отрезков следует проверить свойство существования рассматриваемой фигуры. Если получится хотя бы одна ложь, то треугольник построить нельзя:
Таким образом, для определения возможности существования того или иного треугольника на плоскости необходимо проверить тот факт, что каждая из его сторон имеет меньшую длину, чем сумма двух других отрезков. Теорема косинусов является удобным инструментом для определения количественных характеристик рассматриваемого типа фигур.
О многоугольнике с тремя сторонами
Соотношение углов и сторон в треугольнике интуитивно можно понять, если хорошо представлять эту фигуру. Речь идет о плоском объекте, который состоит всего из трех отрезков. Они расположены таким образом, что начало первого совпадает с концом последнего, то есть они пересекаются. Каждый отрезок представляет собой независимую сторону фигуры. Точка пересечения является вершиной, а соответствующий ей угол является внутренним.
Таким образом, два ключевых элемента образуют рассматриваемую фигуру:
И вершин, и сторон в любом треугольнике по три, поэтому его принято обозначать большими латинскими буквами, например, ABC или MNK. Малые буквы резервируют для обозначения длин сторон, например, a, b, c.
На первый взгляд может показаться, что рассматриваемый объект является несложным, и в нем нечего изучать. Действительно, он является самым простым по построению многоугольником, однако, он обладает большим количеством свойств, количественное и качественное знание которых требуют понимания многих теорем.
Существование фигуры
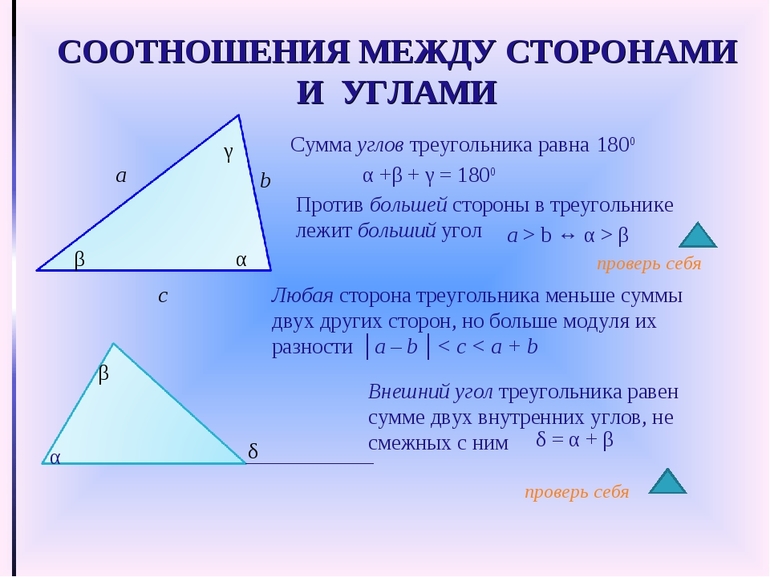
Пусть имеется три отрезка, и необходимо понять, возможно ли из них построить треугольник. Это можно сделать с помощью одного простого правила, которое можно сформулировать следующим образом: любая сторона треугольника всегда меньше суммы длин двух других.
Знание этого правила является очень важным и эффективным инструментом при решении задач. Например, из отрезков с условными длинами 1, 2 и 4 построить треугольник невозможно, а из 2, 3, 4 это сделать можно.
Помимо соотношения длин сторон существует также еще одна теорема, которая гласит, что во всяком треугольнике сумма его внутренних углов всегда равна 180 °. Благодаря знанию этой теоремы можно все рассматриваемые фигуры разделить на три типа:
Полноты ради следует сказать о вырожденных фигурах. К ним относятся такие многоугольники, у которых тупой стремится к 180 °. Несложно представить, что в этом случае два других будут обращаться в ноль, а сумма противолежащих им сторон окажется равной длине отрезка, расположенного напротив тупого угла. На плоскости вырожденный треугольник представляет отрезок, его площадь стремится к нулю.
Важные линии
Несмотря на всю простоту построения треугольника, при решении задач могут понадобиться дополнительные отрезки. Внутри фигуры существует целая гамма типов этих отрезков, наиболее важными из них являются следующие:
Для правильных, равнобедренных и прямоугольных треугольников некоторые из названных отрезков могут совпадать друг с другом, а также со сторонами фигуры. Например, в прямоугольном треугольнике две малые стороны (катеты) также являются высотами.
Соотношение отрезков и углов
Задачи на соотношение отрезков и угловых мер в рассматриваемой фигуре могут требовать либо качественный, либо количественный ответ. В первом случае следует провести определенное доказательство, опираясь на известные аксиомы и теоремы о сторонах треугольника и их следствия. Во втором же случае следует пользоваться формулами и выражениями, которые содержат тригонометрические функции. В действительности оба типа задач связаны между собой. Так, прежде чем использовать какую-либо формулу, следует доказать возможность ее применения в конкретной ситуации.
Большие и меньшие длины
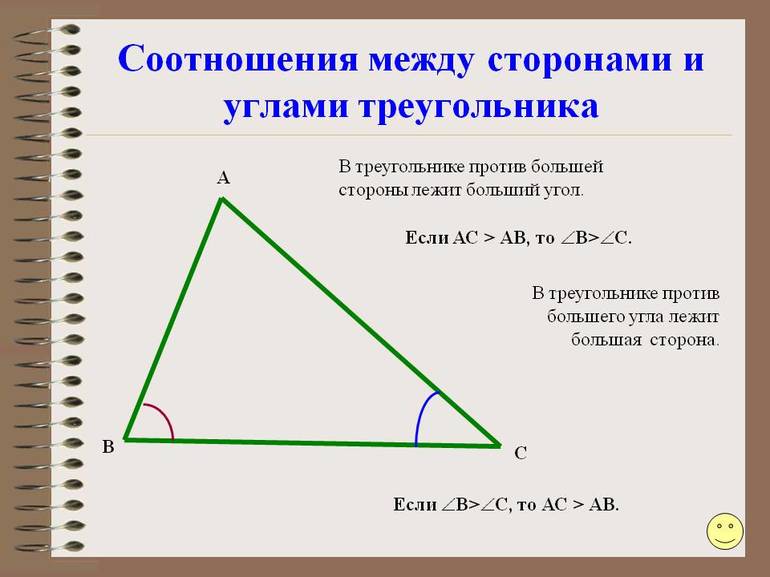
Основная теорема о соотношении между элементами в рассматриваемом типе многоугольников гласит, что против большего угла лежит большая сторона. Ее доказательство провести несложно, если построить треугольник, например, тупоугольный. Из тупого провести отрезок к противоположной стороне таким образом, чтобы он образовывал новый равнобедренный треугольник внутри исходного. После этого следует воспользоваться тем свойством, что внешний угол треугольника всегда больше внутреннего.
Следуя условию равенства углов в построенном равнобедренном треугольнике, легко показать, что против тупого всегда находится самый длинный отрезок.
Обратно эта теорема также справедлива, то есть против большей стороны треугольника лежит больший угол. Ее справедливость понятна каждому школьнику на интуитивном уровне, а доказательство заключается в переборе возможных трех вариантов соотношения между отрезками (больше, меньше, равно) и в привлечении уже доказанной теоремы.
Рассмотренные теоремы приводят к двум важным следствиям:
Рассмотренные теоремы и их следствия активно используются при изучении подобных фигур. Поскольку напротив равных углов двух треугольников лежат соответствующие им длины отрезков, то последние будут попарно относиться друг к другу с определенным коэффициентом подобия.
Теоремы косинусов и синусов
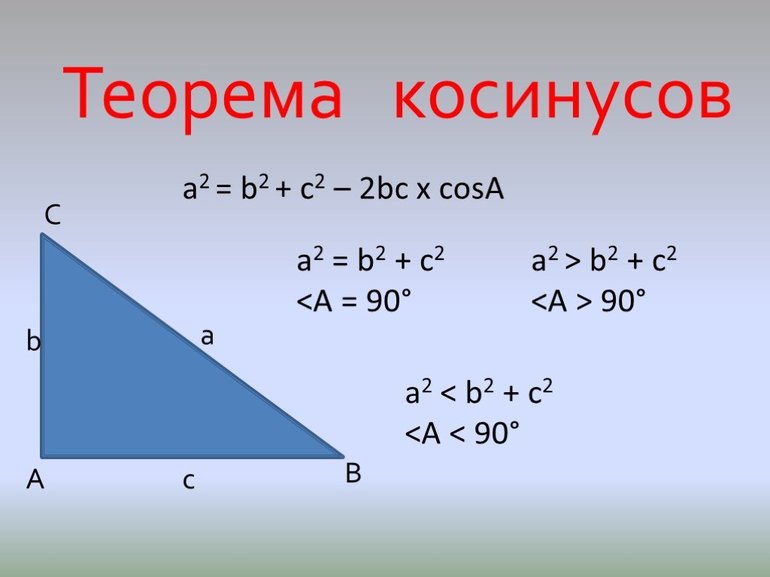
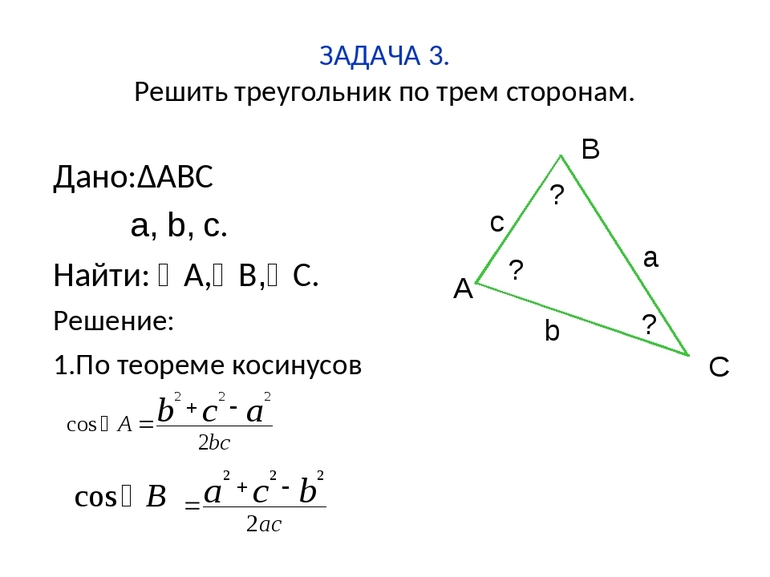
Количественной характеристикой соотношения сторон и углов являются знаменитые формулы, содержащие зависимость длин отрезков и угловых мер. Первая из них называется теоремой косинусов. Соответствующая формула имеет вид:
c 2 = a 2 + b 2 — 2*a*b*cos©.
Здесь величины a, b, c — это длины, C — угол напротив стороны c. Формула позволяет вычислить третью сторону по известным двум другим и углу между ними. Однако, возможности выражения шире, с его помощью можно посчитать всякий внутренний угол фигуры, если известны три ее стороны.
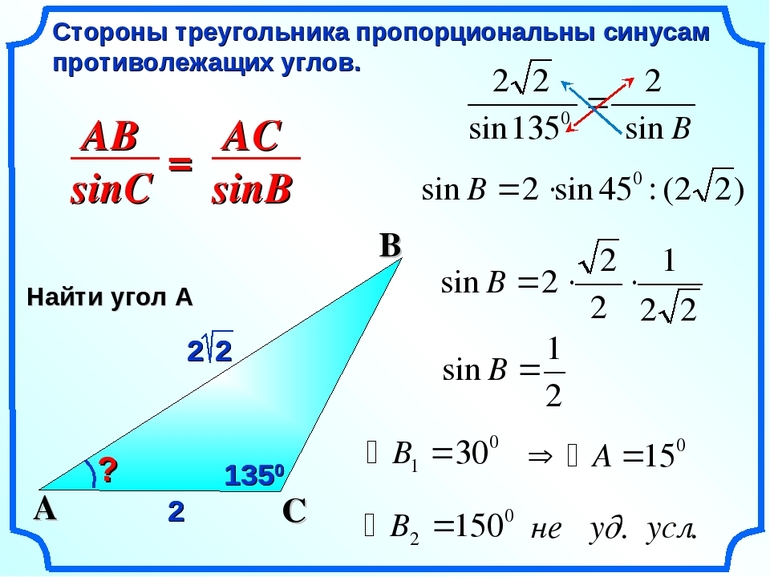
Следующая по счету, но не по важности теорема синусов. Ее математическое выражение записывается так:
a/sin (A) = b/sin (B) = c/sin©.
Эти равенства говорят о том, что отношение стороны к синусу противоположного ей угла является постоянной характеристикой конкретного треугольника. Зная связь двух углов и стороны или двух отрезков и одного угла можно рассчитать все остальные характеристики фигуры. Следует запомнить, что для любого рассматриваемого типа многоугольников однозначное вычисление всех его свойств требует знания минимум трех элементов (кроме трех углов).
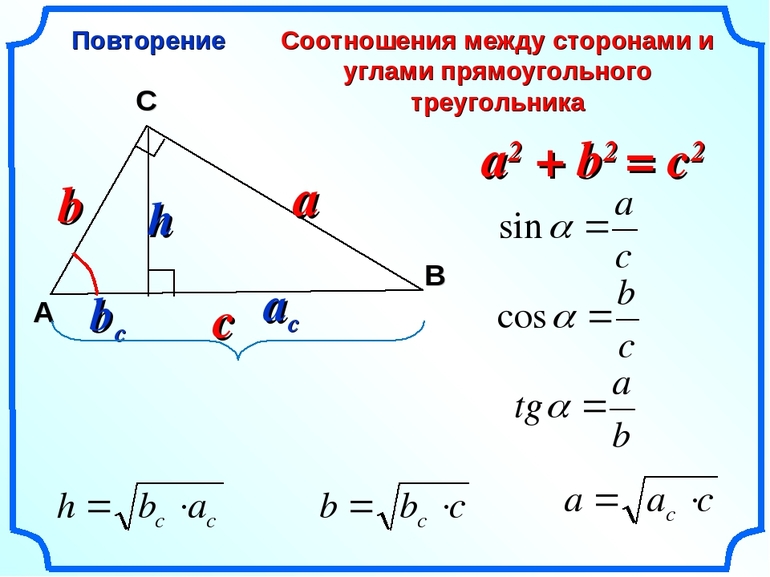
Прямоугольный треугольник
Этот особый случай следует рассмотреть подробнее. Каждый школьник знает знаменитую теорему, позволяющую сравнить соответствие отрезков друг другу в этом типе фигуры. Она гласит, что сумма квадратов катетов соответствует квадрату гипотенузы, и называется пифагоровой теоремой, то есть можно записать:
Работать с прямоугольными треугольниками удобно по одной простой причине: через их геометрические параметры вводятся в математику тригонометрические функции. Последние легко использовать при вычислении сторон и углов фигуры. Например, если фигура является не только прямоугольной, но и равнобедренной, то ее катеты равны, а углы напротив них составляют по 45 °. При этом любой из катетов всегда в 2 0,5 раза меньше гипотенузы:
Это соотношение можно получить также из теоремы Пифагора.
Другая ситуация, когда один из острых углов равен 30 °. Для лежащего напротив него катета a можно записать следующее выражение:
Иными словами, лежащий против 30 ° катет составляет ровно половину длины гипотенузы.
Таким образом, в любом треугольнике существует прямая пропорциональность между длиной стороны и противолежащим ей углом. Для количественного решения задач по геометрии с этой фигурой следует пользоваться выражениями синусов, косинусов и теоремой Пифагора.