Что такое странный аттрактор

СТРАННЫЙ АТТРАКТОР

— притягивающее множество неустойчивых траекторийв фазовом пространстве диссипативной динамической системы. С. а.,в отличие от аттрактора, не является многообразием (т. е. не является кривойили поверхностью); его геом. устройство очень сложно, а его структура фрактальна(см. Фракталы). Поэтому он получил назв. «странный» [Д. Рюэль (D.Ruelle), Ф. Такенс (F. Takens)]. Тот факт, что все траектории, расположенныев окрестности С. а., притягиваются к нему при , принципиально связан с характером неустойчивостей составляющих его траекторий, 0], отвечающих участкам и характеристикиДиода.

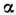
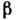
Полезное

Смотреть что такое «СТРАННЫЙ АТТРАКТОР» в других словарях:

СТРАННЫЙ АТТРАКТОР — аттрактор (т. е. притягивающее множество динамической системы )со сложной структурой. Аттрактор компактное инвариантное подмножество фазового пространства, к рое асимптотически устойчиво, т. е. оно устойчиво по Ляпунову, и все траектории из нек… … Математическая энциклопедия

Странный аттрактор — … Википедия

Аттрактор — У этого термина существуют и другие значения, см. Великий аттрактор. Визуальное отображение странного аттрактора Аттрактор (англ. … Википедия

Аттрактор — потенциальное состояние системы, к которому она эволюционирует. По Князевой: конечная область неминуемого схождения фазовых траекторий движения сложной системы. В качестве аттрактора может выступать или точка (устойчивый фокус), или иное более… … Словарь-справочник по философии для студентов лечебного, педиатрического и стоматологического факультетов

Аттрактор странный — аттрактор со сложной геометрической структурой (в частности, с дробной (фрактальной) раздробленностью), на котором близкие траектории расходятся экспоненциально. Движение на странных аттракторах является хаотическим (случайным) … Начала современного естествознания

ТУРБУЛЕНТНОСТЬ — явление, наблюдаемое во мн. течениях жидкостей и газов и заключающееся в том, что в этих течениях образуются многочисленные вихри разл, размеров, вследствие чего их гидродинамич. и термодинамич. хар ки (скорость, темп ра, давление, плотность)… … Физическая энциклопедия

Теория хаоса — У этого термина существуют и другие значения, см. Теория хаоса (значения). Диаграмма раздвоения логистической карт … Википедия

ХАОС ДИНАМИЧЕСКИЙ — (хаос детерминированный) нерегулярное, апериодическое изменение состояния (движение) динамич. системы, обладающее осн. свойствами случайного процесса. Исследования свойств нелинейных динамич. систем показали, что для мн. таких систем характерно… … Физическая энциклопедия

АВТОКОЛЕБАНИЯ — незатухающие колебания, поддерживаемые внеш. источниками энергии, в нелинейной диссипативной системе, вид и св ва к рых определяются самой системой. Термин «А.» введён в 1928 А. А. Андроновым. А. принципиально отличаются от остальных колебат.… … Физическая энциклопедия

СТОХАСТИЧЕСКИЕ КОЛЕБАНИЯ — (от греч. stochastikos умеющий угадывать) нерегулярные, внешне неотличимые от реализации случайного процесса колебанияв полностью детерминированной (без шумов и флуктуации) нелинейной системе. Сложное поведение нелинейных колебат. систем… … Физическая энциклопедия

Источник

Визуализация хаоса: как представляют аттракторы динамических систем

(с)

Среди ученых ходит байка о нетривиальном способе сделать свой доклад интересным и увлекательным. Во время выступления нужно выбрать в зале самого недоумевающего, самого потерянного слушателя, и рассказывать персонально ему, да так, чтобы зажечь в глазах огонек интереса.

Еще известен афоризм, приписываемый физику Ричарду Фейнману: «Если вы ученый, квантовый физик, и не можете в двух словах объяснить пятилетнему ребенку, чем вы занимаетесь, — вы шарлатан».

Доступно объяснять устройство сложных вещей — великий навык, однако бывают истории, о которые сломает язык даже самый искусный оратор. Теория динамических систем – вот та область, где без визуализации чувствуешь себя слепым садовником в окружении колючих, увенчанных шипами растений.

Сложные непериодические режимы поведения динамических систем можно описать непериодическими траекториями — так называемыми странными аттракторами, имеющими фрактальную структуру. Сегодня покажем, как визуализируют поведение странных и некоторых других аттракторов.

Great attractor

Если остановить на улице первого попавшегося человека, посветить ему в лицо фонариком и спросить, что он знает об аттракторах, то, скорее всего, ничего не услышим услышим о Великом аттракторе, притягивающем к себе в глубинах космоса сотни тысяч галактик, чтобы однажды перезапустить Матрицу.

На самом деле космологические аттракторы — это области гравитационной аномалии, вызванные, по всей видимости, особыми галактическими скоплениями, и не имеющие прямого отношения к теме статьи.

Безусловно, стоит отметить, что теория динамических систем особенно хорошо подходит для определения возможных асимптотических состояний различных космологических моделей. Да и видео интересное — посмотрите.

Lorenz attractor

Один из самых знаменитых аттракторов — аттрактор Лоренца, получивший известность благодаря массовому распространению термина «эффект бабочки». Помимо того, что при визуализации аттрактора его форма напоминает бабочку, он представляет собой набор хаотических решений системы Лоренца.

Демонстрация хаотических систем, подобных аттрактору Лоренца (можно сделать самому на C++).

Суть решений Эдварда Лоренца в нелинейной системе обыкновенных дифференциальных уравнений можно передать следующим образом: в любой физической системе при отсутствии совершенного знания начальных условий мы не способны в полной мере предсказать ее будущее. Физические системы могут быть полностью непредсказуемыми даже при отсутствии квантовых эффектов.

Hidden attractor

Аттрактор называется скрытым, если его область притяжения не пересекается с определенной открытой окрестностью точек равновесия. В противном случае он называется самовозбуждающимся аттрактором (self-excited attractor).

Классификация аттракторов (скрытые или самовозбуждающиеся) появилась только в 2009 году — после того как был обнаружен скрытый аттрактор в простейшей электрической цепи Чуа с одним нелинейным резистором, демонстрирующей режимы хаотических колебаний.

Multiscroll attractor

Это целое семейство многокомпонентных аттракторов, включающее в том числе модифицированный скрытый хаотический аттрактор Чуа.

Nonchaotic attractor

Помимо «обычных» хаотических аттракторов существуют периодические, квазипериодические, а также странные нехаотические аттракторы.

Один из основных критериев, по которому аттрактор можно причислить к нехаотическим, — расчет показателей Ляпунова. В этом типе аттракторов для системы экспоненты Ляпунова не являются положительными.

Hyperchaotic attractor

Hyperchaotic attractor — это визуализация дифференциальных уравнений Safieddine Bouali. Гиперхаотические аттракторы существуют только в динамических системах, размерность фазового пространства которых более или равна четырем. Модели гиперхаотических аттракторов могут использоваться в реальных приложениях, имеющих отношение к безопасной связи и шифрованию.

Limit Cycle

Непрерывная динамическая система с изолированной орбитой, подразумевающая самоподдерживающиеся колебания (например, колебания маятниковых часов или сердцебиение во время отдыха).

Rössler attractor

Хаотический аттрактор системы дифференциальных уравнений Рёсслера. В 1976 году врач Отто Рёсслер представил трехмерную модель динамики химических реакций, протекающих в некоторой смеси с перемешиванием. Для аттрактора Рёсслера характерна фрактальная структура в фазовой плоскости.

На аттракторе Рёсслера траектории не пересекают сами себя. Поверхности, образующие странный аттрактор, делятся на отдельные слои, создавая бесконечное множество поверхностей, каждая из которых находится чрезвычайно близко к соседней. Можно допустить, что лента, которая образует основание аттрактора, подобна многослойному листу Мёбиуса.

Spiral attractor

Spiral attractor — аттрактор, позволивший изучить жизнь амеб Dictyostelium discoideum. При истощении питательных ресурсов амебы секретируют циклический аденозинмонофосфат (цАМФ) — сигнальные молекулы, привлекающие соседние клетки к центральному местоположению. Голодные миксамёбы (одноклеточная стадия развития Dictyostelium), подчиняясь сигналам, сползаются к центру, который образовался в результате «склеивания» первых миксамёб, случайно оказавшихся рядом. Соединяясь с помощью молекул клеточной адгезии, они образуют агрегат из нескольких десятков тысяч клеток. Собственно, этот процесс и представлен на видео.

Tinkerbell attractor

Карта Тинкербелла — динамическая система с дискретным временем, демонстрирующая хаотическое поведение в двумерном пространстве. Форму Тинкербелла можно изменить, чтобы получить другие хаотические аттракторы в системах защищенных коммуникаций, использующих хаос связи.

Thomas’ cyclically symmetric attractor

Трехмерный аттрактор, предложенный биоинформатиком Рене Томасом, может рассматриваться как траектория демпфирующей частицы, движущейся в трехмерной решетке сил.

Ikeda attractor

Фрактальный набор, к которому притягивается орбита любой точки на плоскости, если мы продолжаем итерацию определенной карты от плоскости к самой себе.

Заключение

Мы рассмотрели лишь несколько известных типов аттракторов. Всего же вы можете найти упоминания о сотне различных аттракторов.

Надо отметить, что это очень молодая область науки, и поиск, начавшийся с идеи уйти от математической абстракции в сторону практического «создания» хаоса, продолжается по сей день.

Неизменно одно: наш интерес с силой Великого аттрактора притягивают системы, чрезвычайно чувствительные к небольшим отклонениям в описании начального состояния. Мы сталкиваемся с этими системами не из праздного любопытства — мы живем среди них и благодаря им.

Источник

Теория хаоса

Что такое «странные аттракторы» и как они помогают синоптикам

Можно ли прогнозировать хаотическое движение элементов какой-либо системы? От чего зависит хаотическая динамика? Может ли, наконец, взмах крыла бабочки вызвать торнадо? Некоторые важные ответы на эти и другие вопросы нашел американский метеоролог Эдвард Лоренц, (невольный) автор термина «эффект бабочки» и создатель «странного аттрактора». Рассказываем об этом в первом материале, посвященном самым интересным дифференциальным уравнениям.

В 1972 году профессор метеорологии из Массачусетского технологического института Эдвард Лоренц собирался выступить на конференции, но в пылу работы не успел отправить тему своей лекции. Организатор, спешивший разослать приглашения, выбрал заголовок за него: «Предсказуемость: может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?» Так и появился термин «эффект бабочки», известный сегодня всему миру.

Эдвард Лоренц родился в 1917 году в небольшом городке в штате Коннектикут. Изучать атмосферные явления он решил еще в детстве, испытав потрясение от того, с какой легкостью солнечная погода может смениться бурей с громом и молниями.

Путь к исполнению мечты вышел долгим: магистратура в Гарварде, работа метеорологом в авиационном подразделении Армии США, защита диссертации в послевоенный период, наконец, должность научного сотрудника и, позже, профессора в MIT.

В своем выступлении Лоренц выделил несколько ключевых идей:

⦁ Если взмах крыла бабочки может вызвать торнадо, то точно так же на это способны все предыдущие и будущие взмахи, равно как и взмахи остальных миллионов бабочек, не говоря уже об активности бесчисленного населения нашей планеты.

⦁ Если взмах крыла бабочки способен вызывать торнадо, то в равной степени этот же взмах может его предотвратить.

Взмах крыла бабочки в данном контексте должен восприниматься как маленькое изменение начальных условий исследуемой системы, способное как вызвать торнадо, так и изменить его траекторию или вообще стать причиной его затухания.

В отличие от эффекта домино, где конкретное (обычно незначительное) действие приводит к конкретному (обычно значительному) результату, причем происходит это однозначно, взмах бабочки может не иметь никакого влияния на поведение торнадо.

Система Лоренца

Лоренц изучал конвекцию (теплообмен, возникающий за счет движения молекул жидкости или газа) в атмосфере Земли. Для описания подобных физических процессов часто пользуются моделью, которая включает в себя уравнения Навье-Стокса, описывающие движение вязкой ньютоновской жидкости (за исключением некоторых частных случаев, их решения в общем виде на данный момент неизвестны):

⦁ Уравнение движения в векторном виде:

⦁ Уравнение теплопроводности, описывающее распределение температуры в пространстве с течением времени:

⦁ Уравнение непрерывности, которое, по своей сути, описывает принцип сохранения массы чего-либо:

В оригинале эти три составляющие дают следующую систему:

Мы не будем углубляться в детальное объяснение всего вышеизложенного. Достаточно лишь понимать, что это довольно сложная модель, и Лоренцу в результате многостраничных выкладок удалось построить ее упрощение:

Здесь переменная с точкой сверху означает ее производную по времени. Более подробно:

С помощью этой системы уравнений можно рассчитать, как будет вести себя текучая среда, которую равномерно разогревают снизу и охлаждают сверху. Так, как это происходит с воздушными потоками в атмосфере. В частности, она позволяет понять, к какому результату приведет даже небольшое изменение исходных параметров.

Хаотическое движение

Перед тем как приступить к непосредственному анализу полученной системы, рассмотрим некоторые комбинации траекторий. Для наглядности, воспользуемся теми же значениями параметров, что и сам Лоренц: σ = 10, ρ = 28, β = 8/3.

Изобразим движение двух точек, расстояние между которыми изначально невелико:

Довольно интересный результат! Поначалу траектории почти неразличимы, потом они отклоняются совсем ненамного, после чего разница становится уже значительной.

Попробуем еще раз, однако теперь возьмем точки на значительном отдалении друг от друга:

Даже несмотря на подобную разницу начальных условий, траектории попадают на фигуру, которую впоследствии не покидают. Очень странно, их будто что-то притягивает…

Странный аттрактор Лоренца

Действительно, эта фигура так и называется — странный аттрактор Лоренца (от английского attract — «притягивать»).

Формальное математическое определение звучит так: аттрактор — такое подмножество фазового пространства, что все траектории, стартующие не слишком далеко от него, стремятся к нему с течением времени. (Это одно из возможных определений понятия аттрактора, существуют и другие, не эквивалентные данному.)

Слово же «странный» здесь выступает в таком ключе: аттрактор как множество не представим в виде кривой или поверхности, он имеет более сложную, фрактальную структуру. Траектории аттрактора не замыкаются, а малые отклонения постоянно накапливаются, причем экспоненциально.

Сказанное выше можно проиллюстрировать так: две траектории, выпущенные из близких точек, со временем разбегаются достаточно далеко. Причем, чтобы отдалить момент разбегания, например, на одну секунду, нужно уменьшить расстояние между начальными точками, скажем, вдвое. А чтобы на две секунды — вчетверо. А на три — в восемь раз, и так далее.

Это означает, что, даже используя мощный компьютер, мы не можем просчитать траекторию, проходящую вблизи аттрактора, с разумной точностью на протяжении длительного промежутка времени. На каждом шаге вычислений неизбежно вносятся ошибки (из-за округления чисел и погрешностей численных методов), которые быстро накапливаются и приводят к тому, что найденная траектория сильно отличается от настоящей.

Такое искажение невозможно исправить, просто увеличивая мощность компьютера. Подобное явление называется «динамическим хаосом».

Ниже представлена модель странного аттрактора, с которой можно поэкспериментировать, меняя входящие значения. Для желающих более подробно изучить математическую сторону припасен еще один раздел сразу после модели.

Вы можете покрутить модель или увеличить/уменьшить ее масштаб (с помощью кнопок мыши на десктопе или пальцами на экране смартфона). Значение бегунков сверху вниз:

Немного математики

Система Лоренца обладает несколькими замечательными свойствами:

⦁ Правая часть системы не имеет свободных членов, то есть она однородна.

Источник

Визуализация странных аттракторов в Plotly — это шедеврально

Поэзия — это очень красивый, зачастую глубокомысленный слог, которым мы не пользуемся в обыденной жизни, но так им любим наслаждаться. То же самое можно сказать и о математике. В фильме «Пи» главный герой называет математику «языком природы», а в фильме «Игры разума» главный герой говорит о ней, как об «особом виде искусства». Мы же, в обыденной жизни, можем напрочь забыть об этом.

Облик странных аттракторов необычен и притягателен даже в двумерном измерении. Plotly позволяет строить их в трех измерениях, причем он дает возможность очень легко получить именно 3D-модель, которую можно «вертеть» и сквозь которую можно «пролетать» — ощущение «прикосновения».

С чего все началось

Все началось очень давно, где-то в 2007 году в университете я познакомился с теорией самоорганизации и впервые увидел аттрактор Лоренца, его черно-белую иллюстрацию в какой-то книге. Тогда мне показалось слишком странным, что нечто может двигаться по столь необычной траектории. Еще более странным мне казалась сама идея того, что практически все на свете может быть описано одной-единственной теорией.

В общем, все как обычно — мое мировоззрение поменялось, жизнь продолжалась, время шло. И вот, совсем недавно я натыкаюсь на ссылку и вижу вот это:

Изображение взято с сайта chaoticatmospheres.com

«Красиво.» — подумал я. Мысль о том, что все это можно построить в Matplotlib тоже промелькнула, но я уже заранее знал, что ничего впечатляющего не получится. И вот совсем недавно, буквально две недели назад, я познакомился с Plotly и сразу понял, что из этого может что-то получиться.

Первая попытка построения сразу же провалилась. Оказалось, что формулы на некоторых изображениях «Галереи странных аттракторов» содержат ошибки. Впрочем, автор галереи, честно предупреждает о том, что не является математиком, как и автор этой статьи.

Недолгое «гугление» позволило найти вот этот код, который оказался чрезвычайно полезен, а создал его Michael Tyka. Этот замечательный человек сделал целый плагин для Blender-а, позволяющий строить модели (!) 60-ти аттракторов. Фактически, их можно распечатать на 3D-принтере, а учитывая, что есть технологии печати воском, то можно довольно легко получить форму для отливки в бронзе.

Код для визуализации

Что ж, помимо, того что я являюсь математиком-любителем, я так же являюсь любителем-программистом. Так что не судите строго за качество кода.

В результате должна появиться 3D-модель странного аттрактора, называемого Lorenz Mod 1:

Нужно сразу отметить, что для решения систем дифференциальных уравнений была выбрана функция odeint из модуля SciPy, которая показалась мне самым простым и быстрым выходом для создания работающего кода. Однако, все уравнения могут решаться обычным методом Эйлера.

Для обозначения коэффициентов в коде я по привычке использовал названия греческих букв принятых в LaTeX-е. В работе с блокнотами Jupyter это иногда бывает очень полезно, так-как формулы могут быстро стать кодом, а код может быстро превратиться в формулы.

Если вы новичок в экосистеме Python, но хотите, что бы код гарантированно выполнился, то лучше всего установите последнюю версию дистрибутива Python Anaconda, а пакет Plotly через conda — встроенный менеджер пакетов дистрибутива.

Учитывая огромное количество странных аттракторов, построить их все, мне не представляется возможным. Поэтому, в этой статье я приведу лишь самые интересные из тех, что мне удалось построить.

Источник

Странный аттрактор

Оглавление

открытие

Аттракторы уже исследованы для описания динамических процессов. Однако обычно они представлялись как классические геометрические структуры, например точки или циклически пересекаемые линии. Были также известны ациклические аттракторы, но они считались частными случаями аномалий, которые могут возникнуть только при определенном выборе параметров.

С введением концепции странного аттрактора стало возможным лучше понять законы хаотического поведения в динамических системах и описать их количественно. Такое поведение, например турбулентные потоки жидкостей и газов, которое характеризуется отсутствием периодичности и чувствительной зависимостью от начальных условий ( эффект бабочки ), ранее не рассматривалось аналитически из-за его сложности. С помощью таких конструкций, как странные аттракторы, можно математически описать детерминированное, но, тем не менее, непредсказуемое поведение ( детерминированный хаос ).

определение

Мы говорим о странном аттракторе, если выполняются следующие условия:

Примеры

Аттрактор Энона

Относительно простым примером странного аттрактора является аттрактор Энона (названный в честь Мишеля Энона ), который определяется как дискретная система в двумерном пространстве следующими уравнениями:

Глядя на окрестности точки на аттракторе, т.е. ЧАС. круглый диск с небольшим диаметром, он преобразуется этапом визуализации в удлиненный эллипс, который растягивается вдоль линий аттрактора, но имеет меньшую площадь из-за этапа сжатия. Благодаря постоянному применению правила отображения, изображение точечной среды покрывает все большие области аттрактора, в то время как его площадь стремится к нулю.

Аттрактор Рёсслера

Аттрактор Rössler ( обнаружено с помощью Отто Ресслер в 1976 году ) определен в трехмерном пространстве по следующей системе дифференциальных уравнений:

И здесь фрактальная структура создается бесконечной серией операций растяжения и складывания. Если вы посмотрите на траектории двух близких друг к другу точек, они какое-то время будут проходить относительно близко друг к другу, но все больше расходятся в результате растяжения, пока не будет достигнута точка, в которой одна траектория проходит по плоской части. а другой на одном сложенном выше. Между двумя траекториями больше нет связи, мы имеем дело с хаотическим поведением.

Аттрактор Лоренца

Аттрактор Лоренца был обнаружен в 1963 году от Edward N. Lorenz при моделировании воздушных потоков. Он определяется следующей системой уравнений:

Показатель Ляпунова

При численном вычислении первого показателя Ляпунова необходимо принять меры предосторожности, чтобы действительно иметь возможность выполнить любое количество шагов: после каждого шага выполняется перенормировка, т.е. ЧАС. вновь вычисленная возмущенная точка заменяется перед следующим шагом точкой, которая имеет то же направление от невозмущенной точки, но такое же расстояние, как и до шага вычисления. Это предотвращает увеличение начальной ошибки до того порядка, при котором геометрические свойства аттрактора, который в любом случае имеет конечную степень, фальсифицируют результат.

измерение

Важным показателем для фрактала и, следовательно, для странного аттрактора является размерность. Есть несколько способов расширить понятие размерности, которая в классической геометрии может принимать только целочисленные значения, чтобы включить фракталы. В случае классических геометрических объектов все эти определения обязательно должны приводить к их известным размерам, например 1 для линий и 2 для поверхностей. Однако для фрактала разные определения фрактальной размерности также могут давать разные значения.

Размер коробки

Однако этот метод не очень полезен для вычисления размерности странного аттрактора. Чем меньше длина стороны, тем больше элементов пространства учитывается; приходится выполнять множество шагов расчета аттрактора, не зная, все ли элементы пространства, в котором расположен аттрактор, уже записаны. Ошибка вычисления особенно возрастает в диапазонах размеров, которые фактически должны обеспечивать более точные значения.

Информационное измерение

Это среднее значение информации для отдельных пространственных элементов, взвешенное в соответствии с их естественной мерой, или среднее значение информации всех рассчитанных точек аттрактора.

Пространственные элементы, которые распознаются как составляющие аттрактора только на очень поздних этапах вычислений, также содержат лишь небольшую часть аттрактора и предоставляют лишь небольшую часть общей информации системы. Таким образом, ошибка вычисления из-за преждевременного прекращения вычисления, в отличие от определения размеров коробки, значительно снижается.

Ляпуновское измерение

Важность ляпуновской размерности заключается в возможности ее численного расчета. Хотя определение размерностей ящика и информации, особенно в случае многомерных фазовых пространств, скоро достигает своих пределов, определение показателей Ляпунова и, следовательно, размерности Ляпунова часто возможно даже в этом случае.

Источник