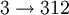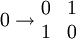Что такое строка туэ морса
Последовательность Туэ – Морса
Есть несколько эквивалентных способов определения последовательности Туэ – Морса.
Прямое определение
Быстрая генерация последовательности
В форме псевдокода:
Результирующий алгоритм требует постоянного времени для генерации каждого элемента последовательности, используя только логарифмическое количество битов (постоянное количество слов) памяти. [2]
Отношение повторения
L-система
Последовательность Туэ – Морса является морфическим словом : [3] это результат следующей системы Линденмайера :
| Переменные | 0, 1 |
|---|---|
| Константы | Никто |
| Начинать | 0 |
| Правила | (0 → 01), (1 → 10) |
Характеризация с использованием побитового отрицания
Подробное изложение первых нескольких шагов:
Бесконечный продукт
Последовательность также может быть определена следующим образом:
Этот степенной ряд является алгебраическим над полем рациональных функций, удовлетворяющих уравнению [12]
В комбинаторной теории игр
Проблема Пруэ – Тарри – Эскотта
Например, для N = 8 и k = 2,
Об обобщении последовательности Туэ – Морса и проблемы Пруэ – Тарри – Эскотта на разбиение более чем на две части см. Болкер, Оффнер, Ричман и Зара, «Проблема Пруэ – Тарри – Эскотта и обобщенные последовательности Туэ – Морса». [13]
Фракталы и графика черепахи
Также можно точно нарисовать кривую, используя следующие инструкции: [15]
Справедливая последовательность
Таким образом, математика поддерживает использование последовательности Туэ – Морса вместо чередования поворотов, когда целью является честность, но более ранние повороты монотонно отличаются от более поздних поворотов некоторым значимым качеством, независимо от того, изменяется это качество непрерывно [18] или дискретно. [20]
В математика, то Последовательность Туэ – Морса, или же Последовательность Пруэ – Туэ – Морса, это двоичная последовательность (бесконечная последовательность нулей и единиц), полученная, начиная с 0 и последовательно добавляя Логическое дополнение последовательности, полученной на данный момент. Первые несколько шагов этой процедуры дают строки 0, затем 01, 0110, 01101001, 0110100110010110 и т. Д., Которые являются префиксами последовательности Туэ – Морзе. Полная последовательность начинается:
Последовательность названа в честь Аксель Туэ и Марстон Морс.
Содержание
Определение
Есть несколько эквивалентных способов определения последовательности Туэ – Морса.
Прямое определение
Чтобы вычислить пй элемент тп, написать номер п в двоичный. Если количество единиц в этом двоичном расширении нечетно, тогда тп = 1, если даже тогда тп = 0. [1] Именно по этой причине Джон Х. Конвей и другие. звонить по номерам п удовлетворение тп = 1 одиозный (за странный) числа и числа, для которых тп = 0 зло (за даже) числа. Другими словами, tп = 0, если п является злой номер и тп = 1, если п является одиозное число.
Генерация быстрой последовательности
В форме псевдокода:
Результирующий алгоритм требует постоянного времени для генерации каждого элемента последовательности, используя только логарифмическое количество бит (постоянное количество слов) памяти. [2]
Отношение рецидива
для всех неотрицательных целых чисел п. [1]
L-система
| Переменные | 0, 1 |
|---|---|
| Константы | Никто |
| Начинать | 0 |
| Правила | (0 → 01), (1 → 10) |
Характеризация с использованием побитового отрицания
Последовательность Туэ – Морса в приведенном выше виде как последовательность биты, можно определить рекурсивно используя операцию побитовое отрицаниеИтак, первый элемент равен 0, а затем, как только первые 2 п элементы были указаны, образуя строку s, затем следующие 2 п элементы должны формировать побитовое отрицание s.Теперь мы определили первые 2 п+1 элементы, и мы рекурсивно.
Подробное изложение первых нескольких шагов:
Бесконечный продукт
Последовательность также может быть определена:
куда тj это jth элемент, если мы начнем с j = 0.
Некоторые свойства
Последовательность Т2п является палиндром для любого п. Далее, пусть qп быть словом, полученным из Т2п путем подсчета единиц между последовательными нулями. Например, q1 = 2 и q2 = 2102012 и так далее. Слова Тп не содержат перекрывающиеся квадраты в результате слова qп палиндром свободные слова.
Этот степенной ряд является алгебраическим над полем формальных степенных рядов, удовлетворяющих уравнению [12]
В комбинаторной теории игр
Проблема Пруэ – Тарри – Эскотта
∑ Икс ∈ S 0 Икс я = ∑ Икс ∈ S 1 Икс я < displaystyle sum _ 
Например, для N = 8 и k = 2,
Условие, требующее, чтобы N быть кратным 2 k+1 не является строго необходимым: есть еще несколько случаев, для которых существует решение. Однако это гарантирует более сильное свойство: если условие выполняется, то набор kй степени любого набора N числа в арифметическая прогрессия можно разбить на два множества с равными суммами. Это непосредственно следует из разложения биномиальная теорема применяется к биному, представляющему п-й элемент арифметической прогрессии.
Об обобщении последовательности Туэ – Морса и проблемы Пруэ – Тарри – Эскотта на разбиение более чем на две части см. Болкер, Оффнер, Ричман и Зара, «Проблема Пруэ – Тарри – Эскотта и обобщенные последовательности Туэ – Морса». [13]
Фракталы и графика черепахи
С помощью черепаха графика, кривая может быть сгенерирована, если автомат запрограммирован с помощью последовательности. Когда члены последовательности Туэ – Морзе используются для выбора состояний программы:
Полученная кривая сходится к Кривая Коха, а фрактальная кривая бесконечной длины, содержащий конечную площадь. Это иллюстрирует фрактальную природу последовательности Туэ – Морса. [14]
Также можно точно нарисовать кривую, используя следующие инструкции: [15]
Справедливая последовательность
Лайонел Левин и Кэтрин Стэндж в своем обсуждении того, как справедливо распределить общий обед, например Эфиопский ужин, предложил последовательность Туэ – Морса как способ уменьшить преимущество движения первым. Они предположили, что «было бы интересно количественно оценить интуицию, согласно которой порядок Туэ-Морса имеет тенденцию давать справедливый результат». [17]
Таким образом, математика поддерживает использование последовательности Туэ – Морса вместо чередования поворотов, когда целью является честность, но более ранние повороты монотонно отличаются от более поздних ходов некоторым значимым качеством, независимо от того, постоянно ли это качество меняется [18] или дискретно. [20]
История
Последовательность Туэ – Морса впервые была изучена Эжен Пруэ в 1851 г., [27] кто применил это к теория чиселОднако Пруэ не упомянул последовательность явно; это было оставлено Аксель Туэ в 1906 году, который использовал его, чтобы основать исследование комбинаторика словЭта последовательность была доведена до всеобщего внимания только благодаря работе Марстон Морс в 1921 году, когда он применил его к дифференциальная геометрия.Последовательность была открыта независимо много раз, не всегда профессиональными математиками-исследователями; Например, Макс Эйве, а гроссмейстер, обладатель титула чемпиона мира с 1935 по 1937 год, и математика учитель, обнаружил его в 1929 году в приложении к шахматы: используя свойство отсутствия кубов (см. выше), он показал, как обойти правило направленная на предотвращение бесконечно затяжных игр путем объявления повторения ходов ничьей.
Последовательность Морса-Туэ
Последовательность Морса-Туэ — бесконечная последовательность нулей и единиц (битов), впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Существует два варианта последовательности, получающиеся друг из друга инверсией битов:
10010110011010010110100110010110… (последовательность A010059 в OEIS) 01101001100101101001011001101001… (последовательность A010060 в OEIS)
Последовательность Морса-Туэ является простейшим примером фрактала и находит свое применение в алгоритмах фрактального сжатия изображений.
Содержание
Определения
Последовательность можно определить многими разными эквивалентными способами:
История
Последовательность была открыта в 1851 году Пруэ (P. Prouhet), который нашёл ей применение в теории чисел, однако не описал исключительные свойства последовательности. И только в 1906 году Аксель Туэ при изучении комбинаторики открыл её заново.
Публикация работы Туэ в Германии прошла бесследно, и последовательность вновь открывает Марсон Морс (Marston Morse) в 1921 году, применив её в дифференциальной геометрии.
Последовательность открывалась независимо много раз: например гроссмейстер Макс Эйве открыл её применение в шахматах, показав, как играть бесконечно, не нарушая правил ничьи.
Свойства
Симметрии
Как и любой фрактал, последовательность Морса-Туэ обладает рядом симметрий. Так последовательность остаётся сама собой
Другие свойства
где ti — элементы последовательности Морса-Туэ. Это число трансцендентно (доказано K. Mahler в 1929 году).
Вариации и обобщения
Обобщение на произвольный алфавит
Имея произвольный алфавит из n символов, можно составить ровно n разных циклических перестановок этого алфавита. Затем, заменя каждую букву алфавита на соответствующую перестановку, можно получить последовательность Морса-Туэ. Так например из трёх симоволов 1, 2, 3 можно составить три циклических перестановки: 123, 231, 312:


Многомерное обобщение
Многомерная последовательность Морса-Туэ определяется подобным образом. Так например двумерная последовательность (матрица) является пределом последовательности, каждый следующий член которой получается из предыдущего при помощи преобразования

 |
 |
 |
 |
 |
Также двумерную последовательность Морса-Туэ можно представить как совокупность одномерных.
Ссылки
Полезное
Смотреть что такое «Последовательность Морса-Туэ» в других словарях:
Последовательность Морса — Туэ бесконечная последовательность нулей и единиц (битов), впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Существует два варианта последовательности,… … Википедия
Последовательность Пруэ-Туэ-Морса — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
Последовательность Туэ-Морса — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
Последовательность Туэ — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
Туэ — Туэ, Аксель Аксель Туэ Аксель Туэ (Axel Thue; 19 февраля, 1863 7 марта, 1922) норвежский математик, известный своими работами по комбинаторике и диофантовым уравнениям … Википедия
Туэ, Аксель — Аксель Туэ Аксель Туэ (Axel Thue; 19 февраля, 1863 7 марта, 1922) норвежский математик, известный своими работами по комбинаторике и диофантовым уравнениям … Википедия
Туэ Аксель — Аксель Туэ Аксель Туэ (Axel Thue; 19 февраля, 1863 7 марта, 1922) норвежский математик, известный своими работами в комбинаторике и Диофантово диофантовых уравнениях. См. также Последовательность Туэ Морса Бесквадратное слово … Википедия
Бесповторное слово — Бесквадратное слово (англ. squarefree word) слово, в котором никакое подслово не повторяется подряд 2 раза (т.е. это слово нельзя представить в виде yxxz, где x, у и z некоторые подслова). А. Туэ доказал, что бесконечные бесквадратные слова… … Википедия
Бесквадратное слово — (англ. squarefree word) слово, в котором никакое подслово не повторяется подряд 2 раза (т.е. это слово нельзя представить в виде yxxz, где x, у и z некоторые подслова). А. Туэ доказал, что бесконечные бесквадратные слова существуют над… … Википедия
Битовый поток — (англ. bitstream или англ. bit stream) временная последовательность битов. Битовые потоки широко используются в телекоммуникациях и компьютерных технологиях. Например, технология транспортных телекоммуникационных сетей SDH и… … Википедия
Последовательность Туэ
Последовательность Морса-Туэ — бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность является простейшим примером фрактала. Применяется в алгоритмах сжатия изображений фрактальным способом.
Содержание
Определения
Последовательность можно определить многими разными эквивалентными способами:
Свойства
Обобщение на произвольный алфавит
Имея произвольный алфавит из n символов, можно составить ровно n разных циклических перестановок этого алфавита. Затем, заменя каждую букву алфавита на соответсвующую перестановку, можно получить последовательность Морса-Туэ. Так например из трёх симоволов 1, 2, 3 можно составить три циклических перестановки: 123, 231, 312:
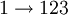
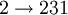
Многомерное обобщение
Многомерная последовательность Морса-Туэ определяется подобным образом. Так например двумерная последовательность (матрица) является пределом последовательности, каждый следующий член которой получается из предыдущего при помощи преобразованием
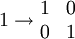
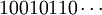 |
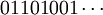 |
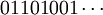 |
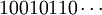 |
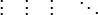 |
Также двумерную последовательность Морса-Туэ можно представить как совокупность одномерных.
Симметрии
Как и любой фрактал, последовательность Морса-Туэ обладает рядом симметрий. Так последовательность остаётся сама собой
Другие свойства
, где ti — элементы последовательности Морса-Туэ. Это число трансцендентно (доказано K. Mahler в 1929).
История
Последовательность была открыта в 1851 году Пруэ (P. Prouhet), который нашёл ей применение в теории чисел, однако не описал исключительные свойства последовательности. И только в 1906 году Аксель Туэ при изучении комбинаторики открыл её заново.
Публикация работы Туэ в Германии прошла бесследно, и последовательность вновь открывает Марсон Морс (Marston Morse) в 1921 году, применив её в дифференциальной геометрии.
Последовательность открывалась независимо много раз: например гроссмейстер Макс Эйве открыл её применение в шахматах, показав, как играть бесконечно, не нарушая правил ничьи.
Применения
Ссылки
Полезное
Смотреть что такое «Последовательность Туэ» в других словарях:
Последовательность Туэ-Морса — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
Туэ — Туэ, Аксель Аксель Туэ Аксель Туэ (Axel Thue; 19 февраля, 1863 7 марта, 1922) норвежский математик, известный своими работами по комбинаторике и диофантовым уравнениям … Википедия
Туэ, Аксель — Аксель Туэ Аксель Туэ (Axel Thue; 19 февраля, 1863 7 марта, 1922) норвежский математик, известный своими работами по комбинаторике и диофантовым уравнениям … Википедия
Туэ Аксель — Аксель Туэ Аксель Туэ (Axel Thue; 19 февраля, 1863 7 марта, 1922) норвежский математик, известный своими работами в комбинаторике и Диофантово диофантовых уравнениях. См. также Последовательность Туэ Морса Бесквадратное слово … Википедия
Последовательность Морса-Туэ — бесконечная последовательность нулей и единиц (битов), впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Существует два варианта последовательности,… … Википедия
Последовательность Морса — Туэ бесконечная последовательность нулей и единиц (битов), впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Существует два варианта последовательности,… … Википедия
Последовательность Пруэ-Туэ-Морса — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
АВТОМАТОВ СПОСОБЫ ЗАДАНИЯ — варианты описания автоматов, их функционирования или поведения. А. с. з. зависят от подхода к определению понятия автомата. При макроподходе (см. Автомат конечный).описывается внешнее поведение автомата; при микроподходе задание должно содержать… … Математическая энциклопедия
Бесповторное слово — Бесквадратное слово (англ. squarefree word) слово, в котором никакое подслово не повторяется подряд 2 раза (т.е. это слово нельзя представить в виде yxxz, где x, у и z некоторые подслова). А. Туэ доказал, что бесконечные бесквадратные слова… … Википедия
Бесквадратное слово — (англ. squarefree word) слово, в котором никакое подслово не повторяется подряд 2 раза (т.е. это слово нельзя представить в виде yxxz, где x, у и z некоторые подслова). А. Туэ доказал, что бесконечные бесквадратные слова существуют над… … Википедия
Последовательность Морса
Последовательность Морса — Туэ — бесконечная последовательность нулей и единиц (битов), впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Существует два варианта последовательности, получающиеся друг из друга инверсией битов:
10010110011010010110100110010110… (последовательность A010059 в OEIS) 01101001100101101001011001101001… (последовательность A010060 в OEIS)
Последовательность Морса — Туэ является простейшим примером фрактала и находит свое применение в алгоритмах фрактального сжатия изображений.
Содержание
Определения
Последовательность можно определить многими разными эквивалентными способами:
История
Последовательность была открыта в 1851 году Пруэ (P. Prouhet), который нашёл ей применение в теории чисел, однако не описал исключительные свойства последовательности. И только в 1906 году Аксель Туэ при изучении комбинаторики открыл её заново.
Публикация работы Туэ в Германии прошла бесследно, и последовательность вновь открывает Марсон Морс (Marston Morse) в 1921 году, применив её в дифференциальной геометрии.
Последовательность открывалась независимо много раз: например гроссмейстер Макс Эйве открыл её применение в шахматах, показав, как играть бесконечно, не нарушая правил ничьи.
Свойства
Симметрии
Как и любой фрактал, последовательность Морса — Туэ обладает рядом симметрий. Так последовательность остаётся сама собой
Другие свойства
где 
Вариации и обобщения
Обобщение на произвольный алфавит
Имея произвольный алфавит из n символов, можно составить ровно n разных циклических перестановок этого алфавита. Затем, заменя каждую букву алфавита на соответствующую перестановку, можно получить последовательность Морса — Туэ. Так например из трёх симоволов 1, 2, 3 можно составить три циклических перестановки: 123, 231, 312:


Многомерное обобщение
Многомерная последовательность Морса — Туэ определяется подобным образом. Так например двумерная последовательность (матрица) является пределом последовательности, каждый следующий член которой получается из предыдущего при помощи преобразования

 |
 |
 |
 |
 |
Также двумерную последовательность Морса-Туэ можно представить как совокупность одномерных.
Ссылки
Полезное
Смотреть что такое «Последовательность Морса» в других словарях:
Последовательность Морса-Туэ — бесконечная последовательность нулей и единиц (битов), впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Существует два варианта последовательности,… … Википедия
Последовательность Пруэ-Туэ-Морса — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
Последовательность Туэ-Морса — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
Последовательность Туэ — Последовательность Морса Туэ бесконечная последовательность нулей и единиц, впервые предложенная в 1906 году норвежским математиком Акселем Туэ в качестве примера апериодической рекурсивно вычислимой строки символов. Эта последовательность… … Википедия
Битовый поток — (англ. bitstream или англ. bit stream) временная последовательность битов. Битовые потоки широко используются в телекоммуникациях и компьютерных технологиях. Например, технология транспортных телекоммуникационных сетей SDH и… … Википедия
Бесквадратное слово — (англ. squarefree word) слово, в котором никакое подслово не повторяется подряд 2 раза (т.е. это слово нельзя представить в виде yxxz, где x, у и z некоторые подслова). А. Туэ доказал, что бесконечные бесквадратные слова существуют над… … Википедия
Бесповторное слово — Бесквадратное слово (англ. squarefree word) слово, в котором никакое подслово не повторяется подряд 2 раза (т.е. это слово нельзя представить в виде yxxz, где x, у и z некоторые подслова). А. Туэ доказал, что бесконечные бесквадратные слова… … Википедия
Индекс — (Index) Определение индекса, виды индексов, расчет индексов Информация об определении индекса, виды индексов, расчет индексов Содержание Содержание Определение Морса Индекс подгруппы Индекс (поисковой машины) Индекс (базы ) Ветро холодовой индекс … Энциклопедия инвестора
Теория катастроф — У этого термина существуют и другие значения, см. Теория катастроф (значения). Теория катастроф раздел математики, включающий в себя теорию бифуркаций дифференциальных уравнений (динамических систем) и теорию особенностей гладких… … Википедия
Теория катастроф (математика) — Теория катастроф раздел математики, включающий в себя теорию бифуркаций дифференциальных уравнений (динамических систем) и теорию особенностей гладких отображений. Термины «катастрофа» и «теория катастроф» были введены Рене Томом (René Thom) и… … Википедия