Что такое структурный синтез

Понятие структурного и параметрического синтеза

Синтез – (греч. synthesis) – соединение, сочетание, составление.

Синтез РЭС заключается в создании формы, структуры, выборе элементов, их размещении с целью получения заданных свойств РЭС, то есть создание конструкции РЭС. При этом конструкция должна отвечать заданным свойствам наилучшим образом, то есть быть оптимальной.

Синтез – определение оптимальной структуры системы (конструкции) при заданных показателях качества и ограничениях [10].

Различают проектные процедуры синтеза и анализа [4, кн.1].

Синтез заключается в создании описания объекта.

Процедуры синтеза делятся на процедуры структурного и параметрического синтеза.

Целью структурного синтеза является определение:

– перечня типа элементов, составляющих объект,

– способа связи элементов между собой в составе объекта.

Процедуры структурного синтеза относятся к наиболее трудноформализуемым в процессе проектирования, в то же время дальнейшее повышение степени автоматизации проектирования зависит от успехов в разработке методов структурного синтеза.

Классификация структурного синтеза:

I В зависимости от стадии проектирования, на которой производится синтез, различают процедуры:

1) выбора основных принципов функционирования будущего объекта;

2) выбора технического решения в соответствии с заданным принципом функционирования;

3) оформления технической документации.

II По типу синтезируемых структур различают задачи синтеза:

3) геометрического синтеза.

При одномерномсинтезе решаются задачи упорядочения элементов структуры в одномерных пространствах (задача составления расписания).

При схемном синтезе определяется структура объекта без конкретизации его геометрических форм (синтез кинематических, электрических схем).

При геометрическомсинтезе определяются геометрические свойства проектируемых объектов и решаются задачи позиционирования, синтеза поверхностей, синтеза траекторий.

К задачам позиционирования относят задачи взаимного расположения в пространстве деталей заданной геометрической формы, например, задачи выбора баз для механической обработки деталей сложной формы, синтез композиций из заданных деталей.

К синтезу поверхностей и траекторий относят задачи проектирования поверхностей (поверхность радиатора, форма несущей, синтез траектории движущихся рабочих органов технологических автоматов).

III В зависимости от возможностей формализации различают пять уровней сложности задач синтеза:

I уровень сложности: выполнение параметрического синтеза (структура задана ТЗ);

II уровень сложности: возможен полный перебор известных решений;

III уровень сложности: комбинаторные задачи;

IY уровень сложности: поиск вариантов структур в счетных множествах неизвестной или неограниченной мощности;

Y уровень сложности: решение задачи проблематично.

Параметрический синтез заключается в определении числовых значений параметров элементов при заданных структуре и условиях работоспособности на выходные параметры объекта, т. е. при параметрическом синтезе можно найти точку или область в пространстве внутренних параметров, в которых выполняются те или иные условия (обычно условия работоспособности).

В проектировании РЭС синтез структуры состоит в выборе совокупности его элементов и формировании связи между ними (ЭРЭ – электрические, информационные связи; несущие элементы конструкции – пространственные, механические связи; теплоотводы – тепловые; элементы крепления – механические связи).

Параметрический синтеззаключается в определении числовых значений параметров РЭС: параметров резисторов, конденсаторов, размеров несущих, теплоотводов. Примером решения задачи параметрического синтеза является известная обратная задача при расчете размерных цепей.

Анализ – (греч. analysis) – разложение, расчленение, разбор.

Анализ заключается в определении свойств и исследовании работоспособности объекта по его описанию, т. е. при синтезе создаются, а при анализе оцениваются проекты объектов.

Процедуры анализа различаются как процедуры одно- и многовариантного анализа.

При одновариантноманализе заданы значения внутренних и внешних параметров, требуется определить значения выходных параметров объекта.

Многовариантный анализзаключается в исследовании свойств объекта в некоторой области пространства внутренних параметров.

В проектировании РЭС ставится задача оптимального синтеза РЭС.

При этом необходимо ответить на ряд вопросов:

– что такое наилучший вариант, по какому признаку или критерию выделяется этот наилучший вариант?

– как определить, математически записать этот критерий?

– каким методом найти оптимум? И здесь же формулирование условий, ограничений, при действии которых должна осуществляться оптимизация.

Если задана совокупность данных (формула 1.2)

,

то задача синтеза заключается в отыскании системы S, удовлетворяющей исходным данным (1.2) и имеющей наилучшее значение .

Источник

Структурный синтез технического объекта

Задача синтеза технического объекта включает в себя создание структуры проектируемого объекта и расчет его параметров. Эти две части синтеза соответственно называются структурным и параметрическим синтезом. Задача структурного синтеза заключается в поиске оптимальной или рациональной структуры (схемы) технического объекта для реализации заданных функций в рамках выбранного принципа действия.

Существо получения математических моделей объектов проектирования электронно-вычислительной и радиоэлектронной аппаратуры, для решения задач структурного синтеза, рассмотрим на примере компоновки, размещения, трассировки.

Задача компоновки

Под задачами компоновки понимают задачи разбиения множества D=(d₁,d₂. d_n) из п элементов на ряд непересекающихся подмножеств D_k, k=1. N, чтобы при этом выполнялись заданные ограничения и достигался экстремум некоторой функции качества F(x).

При заданном числе N подмножеств разбиения задача компоновки формулируется следующим образом:

и для любых k, l, принадлежащих множеству N>выполняется:

(3)

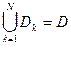
где D_k — множество элементов, принадлежащих k-муподмножеству разбиения при условии, что мощность |D_k| каждого подмножества из разбиения задана, т.е.

Просмотреть все варианты разбиения уже для числа п>100нереально!

Применяя целочисленное программирование, можно уменьшить число просматриваемых вариантов компоновки.

Пусть требуется распределить п компонентов электронной схемы между N блоками таким образом, чтобы суммарное число связей между блоками было минимально.

Пусть функция качества F(x) характеризует общее число связей между подмножествами:

k > для k = 1,N, тогда, задача компоновки запишется:

(5)

(6)

(7)

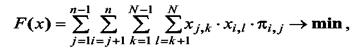
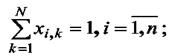
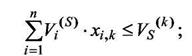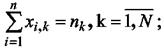
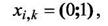(9)

Условия 6 и 7 означают, что каждый компонент может быть отнесен только к одному из подмножеств D_k и в каждом подмножестве D_k может содержаться компонентов не более, чем заданное число n_k.

Задача размещения

Высокая плотность размещения элементов ЭВА создает большие трудности при реализации соединений между ними. В этой связи задача размещения элементов на плоскости определяет быстроту и качество трассировки. Оптимальное размещение элементов обеспечивает повышение надежности проектируемого устройства, минимизацию наводок, задержек сигналов, уменьшение общей длины соединений и т.п.

Формально задача размещения заключается в определении оптимального варианта расположения элементов на плоскости в соответствии с введенным критерием. Например, с минимальной взвешенной длиной соединений.

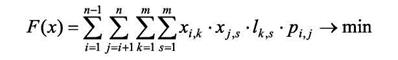Тогда математическая модель задачи размещения может быть записана:

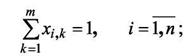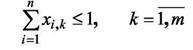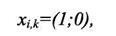Условия 11 и 12 означают, что каждый компонент может быть размещен только на одно посадочное место и каждое посадочное место может быть закреплено только за одним компонентом.

Задача трассировки

Задача трассировки встречается при конструировании печатных плат; разработке систем водоснабжения, электроснабжения и т.д.

Трассировка соединений является, как правило, заключительным этапом конструкторского проектирования ЭВА и состоит в определении линий, соединяющих эквипотенциальные контакты элементов и компонентов, составляющих проектируемое устройство.

Основная задача трассировки формулируется следующим образом: по заданной схеме соединений проложить необходимые проводники на плоскости (плате, типовом элементе замены, кристалле и т.п.), чтобы реализовать заданные электрические соединения с учетом заранее заданных ограничений. Основными являются ограничения

На ширину проводников и минимальное расстояние между ними.

Исходной информацией для решения задачи трассировки соединений обычно являются список цепей, параметры конструкции элементов и коммутационного поля, а также данные по размещению элементов.

Критериями трассировки, наиболее часто используемые для оценки качества решения задачи трассировки, могут быть:

· процент реализованных соединений,

· суммарная длина проводников,

· число монтажных слоев,

· число межслойных переходов,

· минимальная область трассировки и др.

Задача трассировки всегда имеет топологический и метрический аспекты. Топологический аспект связан с выбором допустимого пространства расположения отдельных фрагментов соединений без фиксации их конкретного месторасположения при ограничениях на число пересечений и слоев. Метрический аспект предполагает учет конструктивных размеров элементов, соединений и коммутационного поля, а также метрических ограничений на трассировку.

Пусть U_k — множество точек, соединяемых по электрической цепи a_k;

|U_k| =n_k, где каждому элементу U_k соответствует одна точка в монтажном пространстве.

Введем понятие трассы.

Определим переменную проектирования x_ij

x_ij = 1, если ребро (i,j), длиной l включается в связывающую сеть;

x_ij =0, в противном случае,

где x_ij — булева переменная.

Тогда математическая модель задачи трассировки запишется:

(16)

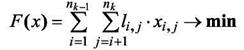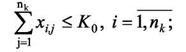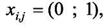
где К₀ — максимально допустимое число соединений в одной точке.

Условие (15) означает, что в одной точке не могут соединяться количество ребер более заданного числа К_0.

Для контроля связности сети при решении задачи трассировки, математическая модель (17,18) может быть дополнена условиями:

Источник

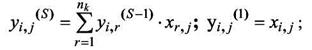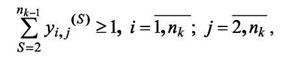Структурный синтез механизмов

Целью структурного синтеза механизма является его структурно-кинематическая схема с минимальным количеством звеньев для преобразования движения заданного количества входных звеньев в тре­буемое движение выходных звеньев. Задачи структурного синтеза многовариантны. Одно и то же преобразование движения можно получить различными по структуре механизмами. При выборе оптимальной структурно-кинематической схемы учитывается технология изготовления звеньев и кинематических пар, требования по точности изготовления и монтажа механизма, условияего эксплуатации.

Синтез структурно-кинематаческих схем механизмов может осуществляться:

— методом наслоения структурных групп;

—методом инверсии;

— методом конструктивного преобразования.

Метод наслоения структурных групп заключается в том, что к основному двухзвенному механизму, состоящему из входного звена и стойки, присоединяются структурные группы с нулевой подвижностью.

В зависимости от того, какими кинематическими парами они присое­диняются, какова форма звеньевмогут получиться разные варианты механизмов.

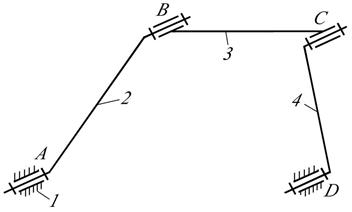
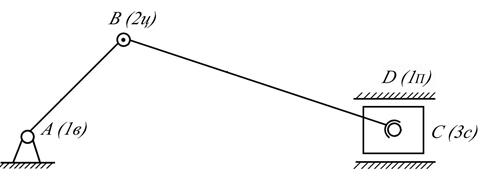
Присоединением к основному механизму, состоящему из входного звена 2 и стойки 1, группы Ассура П класса 1-го вида (звенья 3,4 и кинематические пары B,C,D) получим кривошипно-коромысловый механизм (рис.2.5.).

Если к этому же основному механизму присоединить группу Ассура П класса 2-го вида, то получим кривошипно-ползунный механизм (рис.2.6.)

Присоединяя к полученному механизму еще одну такуюже струк­турную группу, получим схему V-образного двигателя внутреннего сгорания (рис.2.7.).

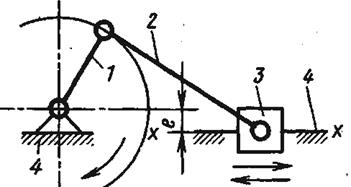
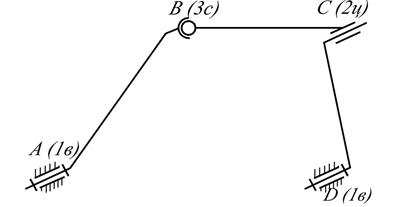
Метод инверсиизаключается в получении различных вариантов механизма путем замены функций одного звена функциями другого звена. Например: инверсиейкривошипно-ползунного механизма (рис.2.8а) можнополучить кривошипно-кулисныймеханизм(рис.2.8б), если стойкой сделать звено 1, а выходным –звено 2.

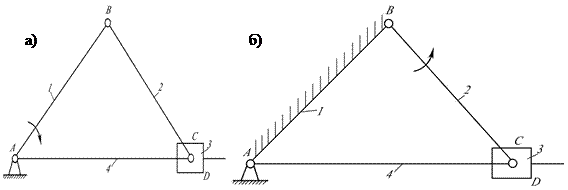Всё выше сказанное относится к плоским статически определимым (т.е. идеальным)механизмам. В идеальном механизме отсутствуют избыточные связи. Однако, вследствие неточности изготовления, идеальный плоскиймеханизм становится, в некоторой степени, пространственным,поэтому при структурном анализе механизма целесообразно использовать формулу Сомова-Малышева, подставляя в нее подвижность идеального механизма и выявляя количество избыточных связей.

При проектировании кривошипно-ползунного механизма взята структурная схема, состоящаяиз исходного механизма (1,4) и 2-х поводковой группы (2,3) с кинематическими парами 5 класса (рис.2.9). Подвижность этого механизма по формулеЧебышева

Если теперь принять,что, из-за неточностей изготовления этот механизм пространственный,то по формуле Сомова-Малышева найдем число избыточных связей:

g = W – 6(k – 1) + I × p_i = 1 – 6(4 – 1) + 5 × 4 = 3

Избыточные связи не меняют степени подвижности механизма, но при его работе могут вызвать деформация звеньев. Как устранять избыточные связи? Это можно сделать повышая подвижность кинематических пар.

Заменим одноподвижную вращательную кинематическую пару В на 2-х подвижную цилиндрическую, а одноподвижную кинематическую пару Сна 3-х подвижную сферическую.

В преобразованном механизме число избыточных связей равно нулю:

g = 1 – 6 × 3 + 5 × 2 +4 × 1 + 3 ×1 = 0

Рассмотрим еще один пример.

Плоский 4-хзвенный механизм с одноподвижными вращательными кинематическими парами (рис.2.10а) с учетом неточностей изготовления (напри­мер, вследствие не параллельности осей A и D) оказывается пространственным. Сборка кинематических цепей 4, 3, 2 и отдельно 1, 4 не вызывает трудностей. Однако, соединить звенья I и 2 в кинематичес­кой паре В (одноподвижная вращательная) можно будет только путем угловых деформаций звеньев.

Определим число избыточных связей по формуле Сомова-Малышева:

g = 1 – 6 × 3 + 5 × 4 = 3

а

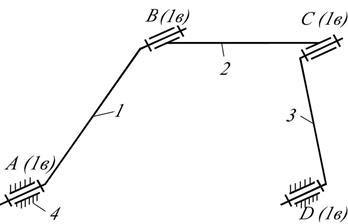
т.е. в данной схеме имеется 3 избыточные связи. Устраним эти связи заменяя одноподвижную вращательную кинематическую пару Сна двухподвижную цилиндрическую, а одноподвижную вращательную пару В на 3-х подвижную сферическую. Это делаетвозможным без деформаций соединить звенья 2 и 1, т.к. звено 2 получило возможность перемещаться вдоль оси цилиндрического шарнира (рис. 2.10 б).

Структурный синтез может быть произведен так же путем конструктивного преобразования механизма (изменения соотношений размеров, формы, расположения звеньев). Это приводит к качественно иным техни­ческим решениям при сохранении струк­турной схемы или вида механизма.

В основу конструктивного преобразования положено совмещение функций звеньев, выполнение элементов шарниров и других кинематических пар большими по размерам, чем размеры звеньев, замена охватывающих элемен­тов охватываемыми, размещение одних звеньев и элементов кинематических пар внутри других элементов ки­нематических пар, замена одних звеньев и кинематических пар другими звеньями и парами с теми же функ­циональными признаками.

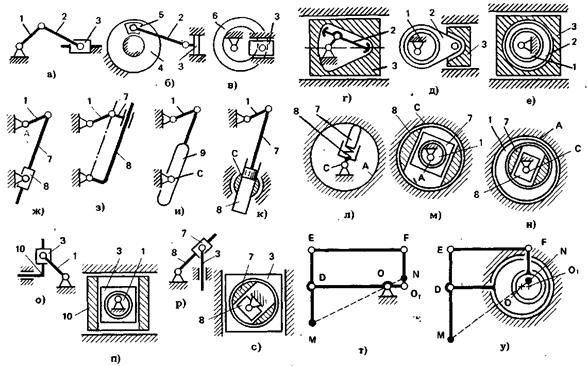
На сх. а — структурная схема кривошипно-ползунного механизма: 1 — кривошип; 2 — шатун; 3 — ползун. На сх. б вместо кривошипа выполнен круговой паз. 4, в котором размещен ползун 5. На сх. в кривошип и шатун заменены кулачком б, который взаимодействует с элементом шарнира 3. Таким образом, кривошипно-ползунный механизм преобразован в кулачковый механизм.

На сх. г элементы шарнира, соединяю­щие звенья 2 и 3, выполнены больше шатуна 2, а кривошип 1 и шатун 2 раз­мещены внутри ползуна.

На сх. д кривошип 1 выполнен в виде эксцентрика и помещен внутрь охваты­вающей детали шарнира 1—2.

На сх. е кривошип 1 и шатун 2 вы­полнены в виде эксцентриков. Элементы шарниров и звенья размещены внутри ползуна. Такая конструктивная разно­видность имеет большую жесткость в направлении движения ползуна, но более низкий КПД из-за больших углов давле­ния и скоростей скольжения, обуслов­ленных соотношением размеров, по сравнению со схемами, рассмотренными выше.

В сх. ж и з кулиса 8 выполнена соответственно в виде охватывающей и в виде охватываемой деталей, а ползун 7 — наоборот: в виде охватываемой и охватывающей деталей.

В сх. и функции кулисы и ползуна совмещены в звене 9, взаимодействую­щем с элементом шарнира С.

В сх. к ползун и кулиса выполнены в виде поршня 7 и цилиндра 8, разме­щенного внутри шарнира С.

В сх. л функции кривошипа и шар­нира А совмещены в элементе шарнира А, охватывающем все остальные детали. Центр кривизны поверхности А смещен по отношению к центру шарнира С. Ползун 7 с поверхностью А образует высшую кинематическую пару. Кривошипно-кулисный механизм такого типа широко используется в гидромашинах.

В сх. м кривошип 1 выполнен в виде эксцентрика и помещен внутрь ползуна 7, который размещен внутри кулисы 8. Все звенья вместе помещены внутрь шарнира С.

В сх. н выполнено преобразование в обратном порядке по отношению к сх. м. Кулиса 8 размещена в ползуне 7, который находится внутри кривошипа I, выполненного в виде эксцентрика. Все звенья размещены внутри шарнира А.

Принципы, приведенные выше, ис­пользованы при преобразовании сх. о в сх. и и сх. р в сх. с.

В сх. п кривошип 1 в виде эксцент­рика помещен внутрь ползуна 3, который расположен внутри ползуна 10.

В сх. с кулиса 8 помещена внутрь ползуна 7, который находится внутри шарнира 7—3, установленного внутри ползуна 3.

В сх. у шарнир 01 размещен внутри шарнира О. Остальные шарниры О, Е, Р оставлены без изменений по сравнению со сх. т. Воспроизводящая точка М, лежащая на линии МО, размещена на звене ОР также внутри шарнира О. В такой схеме добиваются самоторможения звеньев при внешнем воздействии на звено ОР приложенном в т. N.

Приведенные приемы могут быть ис­пользованы по отношению к другим механизмам. Они позволяют получать механизмы с различ­ными габаритными размерами, силовы­ми и энергетическими характеристи­ками.

Вопросы для самоконтроля:

1. Назовите методы структурного синтеза механизмов.

2. В чем состоит метод наслоения структурных групп?

3. В чем состоит метод инверсии?

4. Как методом наслоения структурных групп получить кривошипно-ползунный или кривошипно-коромысловый механизм?

5. Как инверсией кривошипно-ползунного механизма получить кривошипно-кулисный механизм?

6. Как определить количество избыточных связей в механизме?

7. За счет чего устраняются избыточные связи?

8. В чем заключается метод конструктивного преобразования механизма?

Источник

Методы структурного синтеза

Синтез ВС и вычислительных процессов (ВП) включает три этапа:

· выбор типовых элементов структуры (синтез базиса);

· построение структуры (структурный синтез);

· параметризация элементов структуры (параметрический синтез).

Выбор типовых элементов структуры выполняется эмпирически. Для формализации используют матрицу «элементы — свойства» (или, что то же самое, матрицу «средства — цели»). Строкам этой матрицы соответствуют различные альтернативные элементы, выполняющие одни и те же функции, а столбцам — свойства этих элементов, важные для проектируемой ВС (ВП). В каждой клетке матрицы по балльной системе проставляется экспертная оценка i-го свойства у j-го элемента. Анализ этой матрицы проектировщиком позволит составить наглядное и достаточно полное представление о приемлемости того или иного элемента.

Структурный синтез редко бывает полностью независим от параметрического, обычно выбор структуры и определение значений параметров ее элементов тесно связано, составляя вместе структурно-параметрический синтез. Тем не менее, структурный синтез можно выполнять независимо от параметрического в тех случаях, когда формирование определенной структуры объекта является необходимым условием его работоспособности, а параметры лишь обеспечивают более высокое качество функционирования. К таким случаям относятся, например, структурный синтез цифровых устройств, вычислительных процессов. Рассмотрим типовые приемы структурного синтеза.

1) Выбор из готовых структур-прототипов. Этот прием предполагает наличие библиотеки готовых структур. Основной недостаток — необходимость прямого перебора всех структур. Если подобрать полностью подходящую структуру не удается, выбирают наиболее близкую и модифицируют ее под заданные требования путем удаления или добавления новых элементов, введения дополнительных или исключения ненужных связей и т. д.

2) Построение частной структуры из общей. В этом случае сначала создают структуру с максимальной избыточностью, являющуюся обобщением всех известных структур объекта данного типа. Нужная структура синтезируется путем удаления лишних элементов и связей обобщенной структуры. Этот прием традиционно используется при синтезе вычислительных процессов, когда обобщенный процесс представляет собой цепочку всех вычислительных операций, применяемых для изготовления объекта данного класса, а синтез состоит в выборе из этой цепочки только тех операций, которые нужны в каждом конкретном случае. Так как выбор выполняется самим разработчиком на основе своего опыта, этот прием, как и предыдущий, относится к методам эмпирического синтеза.

3) Направленный поиск по И—ИЛИ «дереву». Этот прием можно рассматривать как специальный случай построения частной структуры из общей. В качестве общей структуры выступает заранее составленное И—ИЛИ «дерево», в котором каждая группа путей от корневой вершины через вершины И, ИЛИ до терминальных вершин соответствует одной частной структуре
(рис. 3.5). Синтез по И—ИЛИ «дереву» удобно применить в тех случаях, когда объект легко декомпозируется на составляющие его части, которые декомпозируются на еще более мелкие и т. д., каждая декомпозиция порождает вершину типа И, а каждый уровень декомпозиции — ярус «дерева» из вершин И. Альтернативные варианты реализации каждой части объекта порождают вершину типа ИЛИ. Ветви «дерева», выходящие из вершин ИЛИ — имена способов реализации этих частей или их свойств, играющих определенную роль при синтезе. В качестве примера на рис. 3.5 приведено «дерево» И—ИЛИ для некоторого абстрактного объекта, который декомпозируется на части а, b, затем каждая из них соответственно на части c, d и e, f, g, h.

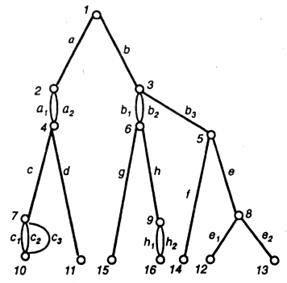
Рис. 3.5 – Структура И-ИЛИ дерева, где
1, 4, 5, 6 – вершины И; 2, 3, 8, 9 – вершины ИЛИ;
10, 11, 12, 13, 14, 15, 16 – терминальные вершины

Части a, c, h могут быть реализованы соответственно способами a₁, a₂, c_1, c₂, h₁, h₂. При этом способ декомпозиции части а на с и d не зависит от способа реализации части а (a₁ или a₂), тогда как способ декомпозиции части b — зависит (при реализации b₁, то b делится на е и f, а при реализации b₂ или b₃ — на g и h). Очевидно, если «дерево» состоит только из вершин И, то оно описывает одну структуру объекта. Альтернативный выбор структуры определяется вершинами ИЛИ. Обход «дерева» из вершин ИЛИ возможен либо в глубину, либо в ширину. При этом с каждой альтернативной реализацией (a₁ или a₂; c₁, c₂ или c₃ и т. д.) связывается оператор перехода, разрешающий переход в следующую вершину И только при выполнении определенных ограничений в вершине ИЛИ. Ограничения могут быть глобальными, относящиеся ко всему объекту (общая масса или общая стоимость ВС, общее время вычислительного процесса и т. д.), и локальными, относящимися к данной реализуемой части объекта (условия стыковки с другими ЭВМ, ВС; ограничения на параметры части ВС).

Условием успешного окончания синтеза является прохождение по всем вершинам И до терминальных вершин. Практически строить «дерево» И— ИЛИ не обязательно, достаточно иметь «дерево» декомпозиции И, в каждой вершине которого нужно программно проверять альтернативные возможности реализации, задаваемые списком этих реализаций и списком ограничений. Отметим, что проверка этих ограничений означает, что синтез носит структурно-параметрический характер, поскольку в процессе синтеза отбираются элементы с определенными значениями параметров.

Направленный поиск по «дереву» состояний и свойств. Структурно-параметрический синтез можно выполнить не только на основе И—ИЛИ «дерева», но и с помощью «дерева» состояний и свойств (рис. 3.6).

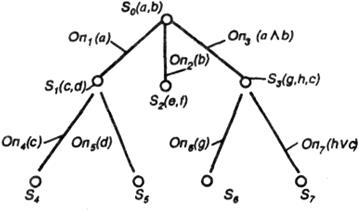
Рис. 3.6 – Дерево состояний и свойств

Каждая вершина в этом «дереве» трактуется как задача, возможное решение которой обладает свойствами , а каждый оператор перехода имеет смысл: «Если решение задачи -1 должно обладать свойством а, то перейти к решению задачи ». Таким образом, чтобы решение задачи обладало свойством , нужно решить задачу , а чтобы решение задачи обладало нужным свойством , нужно решить задачу . Корневое состояние имеет смысл исходной задачи, промежуточные состояния , — смысл промежуточных задач, на которые разбивается исходная задача синтеза, а , , , , — смысл базовых, терминальных, неделимых далее подзадач. Рассмотрим методику синтеза. Пусть известно, что решение должно одновременно удовлетворять свойствам (а, b, h, с). Нужно найти терминальную вершину, имеющую указанные свойства.

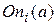
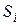
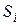
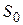
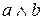
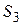
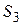
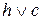
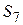
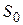
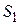
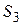
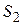
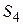
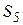
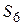
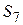
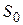
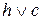
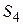
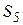
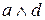
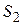
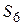
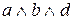
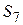
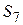
Решение заключается в поиске пути от к той терминальной вершине, которая обладает указанными свойствами a, b, . В этом случае имеем ( ), ( ), (b), ( ), ( , решение должно привести в . Приведенный пример позволяет иллюстрировать некоторые характерные особенности обработки знаний в ИИ при использовании «дерева» состояний.

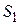
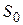
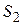
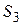
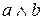
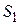
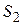
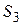
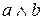
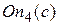
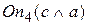
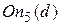
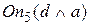
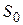
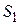
1) Наследование свойств. Из рис. 3.6 видно, что состояние (c, d) на самом деле кроме свойств с, d должно также обладать и свойством а предыдущей вершины состояние (e, f) — свойством b, а состояние (d, h, c) — свойством . Вследствие этого более точным было бы обозначение этих состояний в виде (c, d, a), (e, f, b), (d, h, c, ). Аналогично можно было бы уточнить запись операторов в виде ; в виде и т. д. Обеспечиваемое последовательным прохождением вершин при поиске по «дереву» передача свойств отцовской вершины к дочерним называется в ИИ «наследованием свойству). Механизм автоматического наследования свойств позволяет упростить запись и реализацию операторов перехода, не учитывая в них свойств предыдущих состояний. Он «по умолчанию» обеспечивает присутствие в последующих состояниях свойств предыдущих. Заметим, однако, что «наследование свойств» в «дереве» поиска необязательно и его можно отменить, если условиться, что «отцовское» и «дочернее» состояние по своим свойствам друг с другом не связаны, например, относятся к понятиям с разной семантикой ( — рабочий, — станок). Если же состояния в «дереве» относятся к одному классу, то механизм наследования свойств позволяет «наращивать» свойства состояний в процессе последовательного раскрытия вершин «дерева». Это особенно важно при решении задач классификации и диагностики.

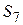
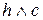
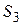
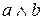
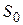
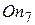
2) Наследование условий перехода. По аналогии с наследованием свойств состояний можно говорить о наследовании условий перехода в операторах перехода On. Это позволяет объяснить результат поиска. Например, приход к состоянию вызван наличием свойства в и одновременно свойства в , что легко установить, анализируя условия перехода в и . Обычно процесс последовательного применения операторов перехода к раскрытию вершин «дерева» состояний запоминается в программе поиска и может быть легко воспроизведен в виде «трассы поиска», вследствие чего процедуру объяснения результатов часто называют «трассировкой поиска».

3) Поиск правил по образцу. Этот часто используемый в работах по ИИ термин означает, что левая часть правила «если 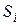-1 обладает свойством а, то переход к » «сравнивается с образцами», т. е. с перечнем фактически имеющихся имен состояний и их свойств. Совпадение левой части правила с каким-либо образцом вызывает активизацию правила, т. е. срабатывание его правой части. Кроме описанных существует большое число других методов синтеза — метод морфологического ящика, весьма близкий к поиску по «дереву» состояний и «И—ИЛИ-дереву», методы «мозгового штурма» и контрольных вопросов, относящиеся к методам решения изобретательских задач, однако в САПР они не получили распространения из-за сложности их формализации.

Дата добавления: 2015-10-29 ; просмотров: 1020 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник