Что такое суперпозиция в физике

Квантовая суперпозиция

Принцип неопределённостиВведение
Математические основы

Основа
Классическая механика · Постоянная Планка · Интерференция · Бра и кет · Гамильтониан

Фундаментальные понятия
Квантовое состояние · Квантовая наблюдаемая · Волновая функция · Квантовая суперпозиция · Квантовая сцепленность · Смешанное состояние ·

Эксперименты
Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга · Проверка неравенств Белла · Фотоэффект · Эффект Комптона

Формулировки
Представление Шрёдингера · Представление Гейзенберга · Представление взаимодействия · Матричная квантовая механика · Интегралы по траекториям · Диаграммы Фейнмана

Уравнения
Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака · Уравнение фон Неймана · Уравнение Блоха · Уравнение Линдблада · Уравнение Гейзенберга

Интерпретации
Копенгагенская · Теория скрытых параметров · Многомировая

Развитие теории
Квантовая теория поля · Квантовая электродинамика · Теория Глэшоу — Вайнберга — Салама · Квантовая хромодинамика · Стандартная модель · Квантовая гравитация

Сложные темы
Квантовая теория поля · Квантовая гравитация · Теория всего

Известные учёные
Планк · Эйнштейн · Шрёдингер · Гейзенберг · Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт

См. также: Портал:Физика

Ква́нтовая суперпози́ция (когерентная суперпозиция) — это суперпозиция состояний, которые не могут быть реализованы одновременно с классической точки зрения, это суперпозиция альтернативных (взаимоисключающих) состояний. Принцип существования суперпозиций состояний обычно называется в контексте квантовой механики просто принципом суперпозиции.

Если функции и являются допустимыми волновыми функциями, описывающими состояние квантовой системы, то их линейная суперпозиция, , также описывает какое-то состояние данной системы. Если измерение какой-либо физической величины в состоянии приводит к определённому результату , а в состоянии — к результату , то измерение в состоянии приведёт к результату или с вероятностями и соответственно.

Из принципа суперпозиции также следует, что все уравнения на волновые функции (например, уравнение Шрёдингера) в квантовой механике должны быть линейными.

Любая наблюдаемая величина (например, положение, импульс или энергия частицы) является собственным значением эрмитова линейного оператора, соответствующим конкретному собственному состоянию этого оператора, то есть определённой волновой функции, действие оператора на которую сводится к умножению на число — собственное значение. Линейная комбинация двух волновых функций — собственных состояний оператора также будет описывать реально существующее физическое состояние системы. Однако для такой системы наблюдаемая величина уже не будет иметь конкретного значения, и в результате измерения будет получено одно из двух значений с вероятностями, определяемыми квадратами коэффициентов (амплитуд), с которыми базисные функции входят в линейную комбинацию. (Разумеется, волновая функция системы может быть линейной комбинацией и более чем двух базисных состояний, вплоть до бесконечного их количества).

Важными следствиями квантовой суперпозиции являются различные интерференционные эффекты (см. опыт Юнга, дифракционные методы), а для составных систем — зацепленные состояния.

Популярный пример парадоксального поведения квантовомеханических объектов с точки зрения макроскопического наблюдателя — кот Шрёдингера, который может представлять собой квантовую суперпозицию живого и мёртвого кота. Впрочем, достоверно ничего не известно о применимости принципа суперпозиции (как и квантовой механики вообще) к макроскопическим системам.

Отличия от других суперпозиций

Квантовую суперпозицию (суперпозицию «волновых функций»), несмотря на сходство математической формулировки, не следует путать с принципом суперпозиции для обычных волновых явлений (поля). Возможность складывать квантовые состояния не обуславливает линейность каких-то физических систем. Суперпозиция поля для, скажем, электромагнитного случая, означает например то, что из двух разных состояний фотона можно сделать состояние электромагнитного поля с двумя фотонами, чего суперпозиция квантовая сделать не может. А полевой суперпозицией состояния вакуума (нулевого состояния) и некой волны будет всё та же волна, в отличие от квантовых суперпозиций 0- и 1-фотонного состояний, являющихся новыми состояниями. Квантовая суперпозиция может быть применима к подобным системам независимо от того, описываются они уравнениями линейными или нелинейными (то есть, справедлив или нет полевой принцип суперпозиции). См. Статистика Бозе — Эйнштейна по поводу связи между квантовой и полевой суперпозициями для случая бозонов.

Также, квантовую (когерентную) суперпозицию не следует путать с так называемыми смешанными состояниями (см. матрица плотности) — «некогерентной суперпозицией». Это тоже разные вещи.

Источник

Квантовая суперпозиция: как физики учатся понимать её правильно

Квантовая суперпозиция — основа квантовой механики

Квантовая механика, зародившаяся в начале XX века и окончательно сформировавшаяся в 1930-х годах, сейчас является хорошо проверенной и чрезвычайно успешной физической теорией. Наша цивилизация немыслима без технических достижений, обязанных своим появлением именно ей. Достаточно упомянуть, что компьютер, ноутбук или смартфон, с помощью которых вы читаете этот текст, никогда бы не были созданы, если бы не было квантовой механики.

Учёным, правда, пришлось заплатить большую цену за эти достижения, поскольку принципы, заложенные в основу квантовой теории, настолько сильно противоречат нашей интуиции, что даже самые сильные умы человечества выбрасывали белый флаг в попытках дать им какое-либо истолкование, которое отличалось бы от знаменитой фразы, приписываемой то Ричарду Фейнману, то Дэвиду Мермину: «Заткнись и считай!».

Одним из таких парадоксальных принципов является принцип квантовой суперпозиции. Вообще, с принципом суперпозиции все мы хорошо знакомы, хотя, возможно, и не называем его так в обыденной жизни. Обычно под суперпозицией понимают простое наблюдение: если одно действие приводит к одному результату, а второе действие — ко второму, то их совместное действие даст оба результата. Например, если вы купите яблоко, и ваш друг купит яблоко, то вместе вы купите два яблока. Принцип суперпозиции, конечно, выполняется не всегда: если в магазине в продаже осталось только одно яблоко, то двух яблок вы с другом никогда не купите, хотя по отдельности купить яблоко могли бы.

Квантовая суперпозиция, однако, существенно отличается от суперпозиции классической. Речь в квантовой теории идёт о суперпозиции не действий, а состояний. Например, если у вас есть две коробки, то электрон может находиться как в одной из них, так и в другой, но кроме того, оказывается, что он может находиться в суперпозиции этих двух состояниях — то есть в некотором смысле — в обоих коробках одновременно. Этот факт, противоречащий всему нашему житейскому опыту, был неоднократно подтверждён в различных экспериментах, причём не только с электронами, но и с более крупными объектами, вплоть до вполне себе макроскопических сверхпроводящих металлических колец, в которых ток одновременно течёт как по часовой, так и против часовой стрелки.

Двухщелевой эксперимент

Классическим примером, демонстрирующим явление квантовой суперпозиции, является опыт с двумя щелями. Этот эксперимент имеет настолько большое значение для понимания квантовой механики, что известный физик Ричард Фейнман в своих не менее известных «Фейнмановских лекциях по физике» называет его явлением, «которое невозможно, совершенно, абсолютно невозможно объяснить классическим образом. В этом явлении таится самая суть квантовой механики».

Суть опыта относительно проста. Пусть имеется источник частиц — это могут быть частицы света фотоны, электроны, атомы, а недавно опыт был проведён и для молекул, — и этот источник освещает непрозрачную для частиц пластинку. В пластинке проделаны две тонкие щели, а сзади неё поставлен экран, на котором прилетевшие частицы оставляют следы. Если мы закроем одну из щелей, то увидим на экране более или менее тонкую полосу напротив второй щели. Если мы закроем вторую щель и откроем первую, результат будет тот же, но полоса появится напротив первой щели. Вопрос в том, что будет, если открыть обе щели одновременно?

Обыденная интуиция подсказывает, что в этом случае на экране мы увидим просто две полосы. Или, если щели расположены достаточно близко друг к другу, одна более толстая полоска, получившаяся просто наложением полос от каждой из щелей. Однако Томас Юнг, который первым осуществил этот эксперимент ещё в начале XIX века, с удивлением наблюдал совсем другую картину. На экране явственно виднелось множество полосок, толщина которых была меньше толщины полос, получавшихся изначально. Сейчас мы называем это интерференционной картиной, а сам эффект — интерференцией на двух щелях.

Интерференционная картина для двух щелей, полученная на современном оборудовании. Что-то подобное Томас Юнг и наблюдал на своём экране. Источник.

Томас Юнг, однако, работал не с отдельными частицами, а с большим их количеством — с ярким источником света. Поэтому хотя его наблюдения и доказали, что свет — это волна, но истинного переворота в мировоззрении не произвели. Учёные просто стали описывать свет как волны. А для волн явление интерференции является естественным. Бросьте в воду два камушка, и вы увидите, что расходящиеся от них круги, пересекаясь, образуют довольно сложный узор, который и будет интерференционной картиной.

Переворот случился в начале XX века. Сначала в теоретических работах Макса Планка и Альберта Эйнштейна была введена гипотеза, что свет состоит из частиц, а затем британскому физику Джефри Инграму Тейлору удалось повторить опыт Юнга, но с настолько слабым источником света, что на экране можно было засечь приход отдельных фотонов. При этом интерференционная картина, получавшаяся после прихода большого количества фотонов, оставалась такой же, как у Юнга. Таким образом, оказалось, что свет вроде бы состоит из частиц, но эти частицы ведут себя как волны.

Ещё сильнее усложнило ситуацию то, что аналогичный эффект был предсказан и для электронов — частиц, от которых уж точно ожидать волновых свойств и явления интерференции не приходилось. И хотя аналог опыта Юнга для электронов был осуществлён только в 1961 году немецким физиком Клаусом Йонссоном, наличие у них волновых свойств было доказано другими методами ещё в 1920-х годах.

Проявление интерференционной картины при облучении двух щелей отдельными электронами. Источник.

Чтобы разрешить создавшееся противоречие, которое получило название корпускулярно-волнового дуализма, учёным пришлось предположить, что каждой частице соответствует некая волна — она получила название волновой функции, — которая зависит от того, в каком состоянии находится частица. Например, если частица прошла через одну щель, то это одно состояние и у него одна волновая функция, а если частица прошла через другую щель, то она находится в другом состоянии и у него другая волновая функция. Принцип квантовой суперпозиции при этом утверждает, что при двух открытых щелях частица находится в состоянии суперпозиции первого и второго состояний, и соответственно её волновая функция — это сумма двух волновых функций. Эта сумма и приводит к возникновению интерференционной картины. В этом смысле говорят, что частица проходит сразу через обе щели, поскольку если бы она проходила только через одну из них, то интерференционной картины бы не было.

Удивительно, но, несмотря на то, какую роль в квантовой физике играет двухщелевой эксперимент, многие учёные понимают его не совсем правильно. Более того, это некорректное объяснение присутствует в большинстве учебников по квантовой механике. Дело в том, что обычно явление суперпозиции в этом опыте объясняют так: волновая функция состояния, в котором находится электрон, прошедший через две щели, является суммой волновых функций состояний, в которых он находился бы, если бы одна из щелей была бы закрыта. Это объяснение, однако, не учитывает, что открывая вторую щель, мы можем изменить то, как электрон проходит через первую. Возвращаясь к примеру с яблоками, представьте, что вы покупаете яблоко на деньги, которые взяли в долг у друга, тогда покупка двух яблок уже не пройдёт так же, гладко, как покупка одним из вас одного яблока, потому что суммарных денег вам может и не хватить.

Трёхщелевой эксперимент: теория

Суть того, что происходит, когда открыто более одной щели, проще объяснить на примере опыта, в котором добавлена ещё одна щель. Кроме того, удобно перейти к альтернативному описанию квантовой физики, придуманному тем же Ричардом Фейнманом. В конце 1940-х годов он показал, что все результаты уже хорошо развитой тогда квантовой механики можно получить, не вводя никаких волновых функций, но предположив, что частица движется из одной точки в другую сразу по всем возможным траекториям, но «вес» каждой траектории, то есть её вклад в окончательный результат, различен и определяется по особым правилам.

Наибольшим весом обладают такие траектории, которые близки к классическим. Например, в случае двух щелей такие траектории показаны на рисунке ниже зелёным цветом.

Но вклад дают и многие другие траектории, и даже такие экзотические, на которых частица часть пути движется назад, а не вперёд. Среди них есть и такие, которые войдя в одну из щелей, затем проходят через другую и выходят через третью, как это показано фиолетовым на рисунке ниже.

Именно наличие таких неклассических траекторий и приводит к тому, что состояние частицы после прохода трёх щелей не равняется простой сумме состояний её прохода через каждую из них в отдельности при закрытых двух других. Отличие, конечно, обычно невелико, но, во-первых, оно может быть существенным, если вас интересуют какие-то слабые эффекты, а во-вторых, его можно усилить, прибегнув к специальным ухищрениям.

Первым на некорректность обычного объяснения принципа суперпозиции для двухщелевого эксперимента указал, по всей видимости, японский физик Х. Ябуки ещё в 1986 году, но его работа долгое время оставалась незамеченной. Современный интерес к этой теме возродила работа 2012 года, опубликованная в авторитетном журнале Physical Review A. В ней авторы рассмотрели случай классической волновой интерференции на трёх щелях на примере электромагнитных волн. Путём прямого численного моделирования фундаментальных для этой области уравнений Максвелла, они показали, что отличие правильного ответа от того, который получается при неправильной интерпретации принципа суперпозиции, в реалистичных условиях составляет около 0,5 %. И хотя эта величина невелика, и измерить её экспериментально пока невозможно, сам эффект является неоспоримым.

Но всё же учёным хотелось бы проверить этот факт и экспериментально, поэтому в 2014 и 2015 годах одна и та же группа учёных, возглавляемая физиком-женщиной из Индии Урбаси Синха, опубликовала две статьи в Physical Review Letters и Scientific Reports, в которых подробно рассмотрела квантовую теорию прохождения частиц через три щели и показала, что эффект несовпадения правильного результата с предсказанием неправильной интерпретации может быть заметно усилен, если проводить измерения с электромагнитными волнами не оптического диапазона, то есть светом, а микроволнового диапазона — такие волны используются, например, в бытовых микроволновых печах для разогрева пищи.

Трёхщелевой эксперимент: практика

Урбаси Синха, комментируя статью 2014 года, утверждала, что её группа уже начала эксперимент с микроволнами, но их результаты до сих пор не опубликованы. Зато совсем недавно вышла статья ещё одной группы учёных, возглавляемых известным физиком Робертом Бойдом (он знаменит, например, тем, что первым осуществил эксперимент с «замедленным» светом). Статья была опубликована в Nature Communications и экспериментально продемонстрировала обсуждаемый эффект. Правда, идея этого эксперимента была другой.

Роберт Бойд и его коллеги предложили усилить «вес» неклассических траекторий вблизи пластинки со щелями за счёт использования так называемых плазмонов. Плазмоны — это что-то вроде «фотонов на привязи», которые могут бегать только вдоль поверхности металла от одной щели к другой. Для этого пластинку со щелями сделали из золота. Золото — отличный проводник, поэтому оно создаёт особо сильные плазмоны.

В эксперименте источник света облучал только одну из трёх щелей. При этом если две другие были закрыты, то наблюдалась типичная картина немного размытой полосы напротив открытой щели. Но когда две другие щели открывались, картина кардинально отличалась: возникала типичная интерференционная картинка со значительно более узкими полосками.

Сравнение изображений на экране в случае, когда две щели из трёх закрыты (слева) и когда открыты все три щели (справа). O. S. Magaña-Loaiza et al., Nat. Commun. 7, 13987 (2016)

Зачем нужны все эти тонкости?

Могут ли эти исследования иметь какое-то практическое значение? Авторы упомянутых работ надеются, что да. Явление квантовой суперпозиции широко используется для так называемой квантовой коммуникации. На её основе, например, работает квантовая криптография. Именно явление суперпозиции даёт неоспоримые преимущества квантовым компьютерам по сравнению с компьютерами, основанными на традиционной электронике. Поэтому в этих направлениях точное понимание того, как работает квантовая суперпозиция, чрезвычайно важно. И именно поэтому можно надеяться, что исследования интерференции на трёх щелях помогут придумать новые, более эффективные протоколы для работы квантовых устройств.

Источник

Принцип суперпозиции электрических полей

Одна из задач, которые ставит электростатика перед собой – это оценка параметров поля при заданном стационарном распределении зарядов в пространстве. И принцип суперпозиции является одним из вариантов решения такой задачи.

Принцип суперпозиции

Предположим наличие трех точечных зарядов, находящихся во взаимодействии друг с другом. При помощи эксперимента возможно осуществить измерение сил, действующих на каждый из зарядов. Для нахождения суммарной силы, с которой на один заряд действуют два других заряда, нужно силы воздействия каждого из этих двух сложить по правилу параллелограмма. При этом логичен вопрос: равны ли друг другу измеряемая сила, которая действует на каждый из зарядов, и совокупность сил со стороны двух иных зарядов, если силы рассчитаны по закону Кулона. Результаты исследований демонстрируют положительный ответ на этот вопрос: действительно, измеряемая сила равна сумме вычисляемых сил согласно закону Кулона со стороны других зарядов. Данное заключение записывается в виде совокупности утверждений и носит название принципа суперпозиции.

Принцип суперпозиции:

Принцип суперпозиции полей заряда является одним из фундаментов изучения такого явления, как электричество: значимость его сопоставима с важностью закона Кулона.

При помощи принципа суперпозиции с использованием закона взаимодействия между точечными зарядами существует возможность определить силу взаимодействия между зарядами, присутствующими на теле конечных размеров. С этой целью каждый заряд разбивается на малые заряды d q (будем считать их точечными), которые затем берутся попарно; вычисляется сила взаимодействия и в заключение осуществляется векторное сложение полученных сил.

Полевая трактовка принципа суперпозиции

Полевая трактовка: напряженность поля двух точечных зарядов есть сумма напряженностей, создаваемым каждым из зарядов при отсутствии другого.

Для общих случаев принцип суперпозиции относительно напряженностей имеет следующую запись:

Инженерная практика подтверждает соблюдение принципа суперпозиции даже для очень больших напряженностей полей.

Все же следует также заметить, что в случае очень малых расстояний (порядка

Например, на поверхности тяжелых ядер при напряженности порядка

10 22 В м принцип суперпозиции выполняется, а при напряженности 10 20 В м возникают квантово-механические нелинейности взаимодействия.

Когда распределение заряда является непрерывным (т.е. отсутствует необходимость учета дискретности), совокупная напряженность поля задается формулой:

В этой записи интегрирование проводится по области распределения зарядов:

Принцип суперпозиции дает возможность находить E → для любой точки пространства при известном типе пространственного распределения заряда.

Примеры применения принципа суперпозиции

Решение

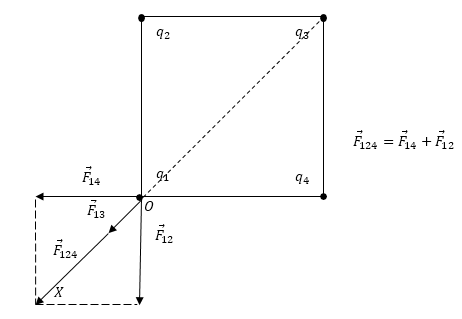
На рисунке 1 проиллюстрируем силы, влияющие на любой из заданных зарядов в вершинах квадрата. Поскольку условием задано, что заряды одинаковы, для иллюстрации возможно выбрать любой из них. Сделаем запись суммирующей силы, влияющей на заряд q 1 :

Силы F 12 → и F 14 → являются равными по модулю, определим их так:

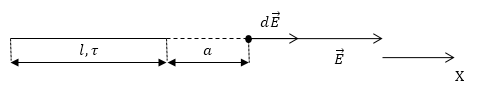
Задан электрический заряд, распределенный равномерно вдоль тонкой нити (с линейной плотностью τ ). Необходимо записать выражение, определяющее напряженность поля на расстоянии a от конца нити вдоль ее продолжения. Длина нити – l .

Решение

В заданной точке все векторы напряженности имеют одинаковую направленность вдоль оси ОХ, тогда:

Условием задачи дано, что заряд имеет равномерное распределение вдоль нити с заданной плотностью, и запишем следующее:

Подставим эту запись в записанное ранее выражение напряженности электростатического поля, проинтегрируем и получим:

Источник