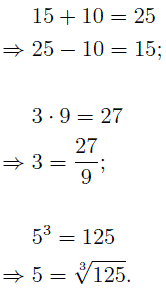Что такое свойства действий в математике

Свойства действий над числами

Сложение

Сложение многозначных чисел производится поразрядно.

Законы сложения.

Пример. 310 + 1454 = 1454 + 310. Каким бы мы способом не складывали результат будет равен 1764.

Пример: (329 + 85) + 120 = 329 + (85 + 120) = 329 + 205 =534;

Вычитание

Свойства действий вычитания:

Задача как пример действий сложения и вычитания

Вычислите удобным способом:

Применяем 2-й и 5-й законы вычитания:

Умножение

Умножить число а на число b (b>1)- значит найти сумму b слагаемых (каждое слагаемое равно а).

Если b = 1, то а x 1 = a.

a (первый множитель) x b (второй множитель) = c (произведение)

Например: 57 + 57 + 57 + 34 + 34 = 57 х 3 + 34 х 2 = 171 + 68 + 239

Законы умножения

Пример. 15 х 110 = 110 х 15.

Пример: (9 х 30) х 10= 9 х (30 х 10) = 9 х 300= 2700;

(65 х 25) х 44 = (25 х 65) х 44 = 25 х (65 X 44)=25 х 2860 = 71500.

a x (b + c) = a x b + a x c;

Задачи как пример действия умножения

Задача 1. Вычислить удобным способом:

1) (37 х 125) х 8 = 37 х (125 х 8) = 37 х 1000 = 37000;

Задача 2. 1 квт/ч стоит 12 руб. Электрический утюг за 1 ч работы расходует 2 квт/ч. Утюгом два дня гладили бельё: в первый день- 3 ч, во второй- 2ч. Сколько стоит электроэнергия, израсходованная за два дня? Задачу решите сами, а мы дадим только ответы: за 3 ч- 72руб; за 2ч- 48руб.

Деление

а (делимое) : b (делитель) = с (частное)

Законы деления:

2224222 : 2222 = 1001

Закон деления суммы (разности) на число:

Пример: (4800 + 9300) : 300 = 4800 : 300 + 9300 : 300 = 16 + 31 + 47.

Закон деления произведения на число:

(а х b) :с = (а : с) х b = (b : с) х а, с не равно 0.

Пример: (125 х 27) : 25 = (125 : 25) х 27 = 5 х 27 = 135.

Свойства действий над числами

Переместительное и сочетательное свойство гласит, что в любой сумме можно как угодно переставлять слагаемые и произвольно объединять их в группы (от перемены мест слагаемых сумма не меняется!).

Распределительное свойство справедливо тогда, когда число умножается на сумму трех и более слагаемых.

Источник

Свойства арифметических действий

Действия

Действие – процесс в математике, в котором по двум данным числам с помощью правила определяют третье число.

Арифметические действия – действия сложения, вычитания, умножения и деления.

В равенстве a + b = c числа a и b называют слагаемыми, число c и запись a + b – суммой.

В равенстве a – b = c число a называют уменьшаемым, число b – вычитаемым, число c и запись a – b – разностью.

В равенстве a • b = c числа а и b называют множителями, а число с и запись а • b – произведением.

В равенстве a : b = с число a называют делимым, число b – делителем, число c и запись a : b – частным.

Свойства

Арифметические действия обладают следующими свойствами.

Переместительное свойство сложения – от перестановки слагаемых сумма не меняется:

Сочетательное свойство сложения – чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел:

Переместительное свойство умножения – от перестановки множителей произведение не меняется:

Сочетательное свойство умножения – чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел:

Распределительное свойство умножения относительно сложения – чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить:

a * (b + c) = a * b + a * c.

Примеры

Вычислим, используя переместительное, а затем сочетательное свойства умножения:

25 • 867 • 4
Используем переместительное, 25 • 867 • 4 = 867 • (25 • 4) = 867 • 100 = 86 700.

329 • 754 + 329 • 246
Имеем: a • b + a • c = a • (b + c).
Тогда: 329 • 754 + 329 • 246 = 329 • (754 + 246) = 329 • 1000 = 329 000.

125 • 24 • 283
Решение. 125 • 24 • 283 = 125 • 8 • 3 • 283 = (125 • 8) • (3 • 283) = 1000 • 849 = 849 000.

Источник

Арифметика. Арифметические действия

Содержание

Арифметика. Арифметические действия

Обратные арифметические действия

Свойства арифметических действий

Порядок выполнения арифметических действий

Умножение натуральных чисел на 10, 100, 1000; и т.д.

Арифметика. Арифметические действия

Арифметическим действием называют операцию, удовлетворяющую ряду свойств и позволяющую по нескольким данным числам найти новое число.

Арифметикой называют науку, изучающую простейшие свойства чисел и арифметических действий.

Существуют шесть арифметических действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

Обратные арифметические действия

Вычитание – это арифметическое действие, обратное к сложению, деление – действие, обратное к умножению, извлечение корня – действие, обратное к возведению в степень.

Свойства арифметических действий

Порядок выполнения арифметических действий

Сложение и вычитание называют действиями первой ступени, умножение и деление – действиями второй ступени, возведение в степень и извлечение корня – действиями третьей ступени.

Действия одной ступени выполняются в том же порядке, в каком они записаны в формуле.

Если в формуле содержатся действия разных ступеней, то сначала выполняют действия высших ступеней, а затем низших ступеней.

Если формула содержит скобки, то сначала выполняют действия в скобках. Скобки бывают круглыми, квадратными и фигурными, причем между ними нет никакой разницы.

Если скобки содержат другие скобки, то сначала выполняют действия во «внутренних» скобках.

Умножение натуральных чисел на 10, 100, 1000 и т.д.

Действительно, например, число 3610 состоит из трёх тысяч, шести сотен и одного десятка, поэтому

Источник

Свойства сложения и вычитания

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

Свойства вычитания

Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.

Уменьшаемое — это число, из которого вычитают.

Вычитаемое — это число, которое вычитают.

Разность — это число, которое получается в результате вычитания.

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

Источник

Сочетай, перемещай, свойства действий

Как найти значение выражения используя свойства арифметических действий?

Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.

Свойства сложения

Переместительный закон сложения

Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:

a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.

Сочетательный закон сложения

Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.

Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.

Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:

Свойства вычитания

Свойство вычитания суммы из числа

Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.

Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …

Свойство сложения разности чисел

Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.

Свойство вычитания разности из числа

Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.

Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.

Свойства умножения

Переместительный закон умножения

Сочетательный закон умножения

Так:
7*3*5 = 5*(3*7) = 5*21 = 105.

Вообще:
abc = а(bс) = b(ас) и т. п.

Умножение числа на произведение чисел

Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.

Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = <[(a·b)•c]•d>…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.

Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.

Умножение числа на сумму чисел

Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.

В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.

Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …

Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.

Распределительный закон умножения для разности чисел

Распределительный закон можно применять и к разности.

Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;

7 • (9 — 6) = 7 • 9 — 7 • 6.

Вообще:
(а — b)с = ас — bc,

а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.

Свойства деления

Деление суммы на число

Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:

Деление разности на число

Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:

Деление произведения на число

Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:

(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:

(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.

Деление числа на произведение

Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:

120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.

а : (bcd …) = [(а : b) : с] : d… и т. п.

Укажем еще следующее свойство деления:

Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3

Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b

Источник

• ← Что такое новое политическое мышление каковы были основные направления этой политики
• Что такое бодяга и как ее использовать →