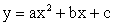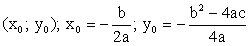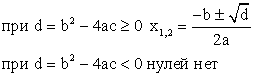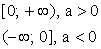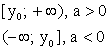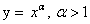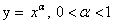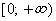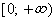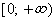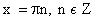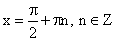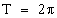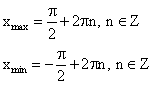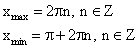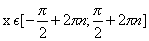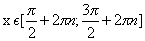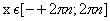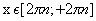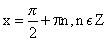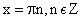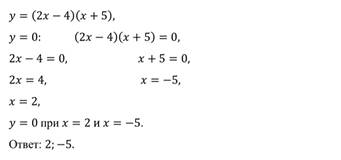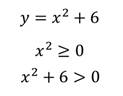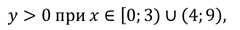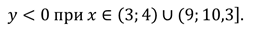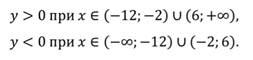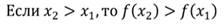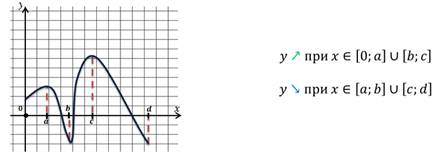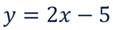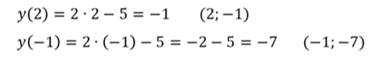Что такое свойства функции
Что такое свойства функции
Функция
Область определения
Вершина параболы
Нули функции
Экстремумы
если a 0, то максимум в вершине
Область значений
Четность
ни четная, ни нечетная
Функция
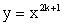
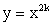
Область определения
Область значений
Четность
Нули функции
Экстремумы
х = 0 — точка минимума
Монотонность
возрастает при х ϵ R
при х ≤ 0 убывает
при х > 0 возрастает
Функция
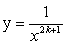
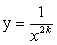
Область определения
Область значений
Четность
Нули функции
Экстремумы
Монотонность
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
возрастает при х ϵ D(f)
возрастает при х ϵ D(f)
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Четность
Периодичность
Экстремумы
Монотонность
Функция
Область определения
R кроме 
R кроме 
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
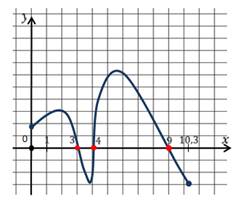
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
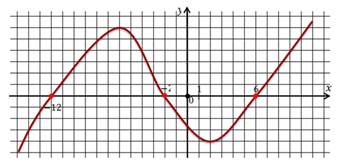
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
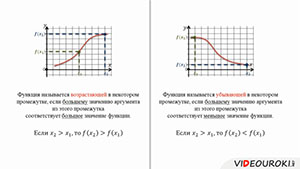
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Основные свойства функций. Справочник репетитора по математике
Д анная страница справочника представляет собой виртуальную шпаргалку по математике для учеников и методическое справочное пособие для репетиторов. Тема «свойства функций», адаптированное для разных уровней учащихся 8-9класов. В нем перечислены определения основных понятий и свойств, виды функций, термины и обозначения, принятые в математике. Репетитору по математике показаны образцы рисунков, которые должны остаться в теради ученика. Информация изложена как на строгом и формальном математическом языке (для среднего и сильного ученика), так на простом (бытовом) уровне, доступном для понимания широкому кругу посетителей сайта. Каждый такой перевод с математического языка на русский отмечен одним из следующих указателей: «пояснение репетитора по математике», «редакция репетитора по математике» или «уточнение репетитора по математике». В этих — переводах вы встретите несколько моих собственных уникальных дополнений и комментариев к классическим фомулировкам, которые я использую на занятиях со слабым учеником.
Определение функции: функцией или функциональной зависимостью называется такое соответствие f (x) при котором числу x из множества X сопоставляется некоторое единственное число из множества Y.
Редакция репетитора по математике: функцией называется закон или правило, по которому можно найти число y (значение какой-нибудь величины), если известно число x (значение какой-нибудь другой величины).
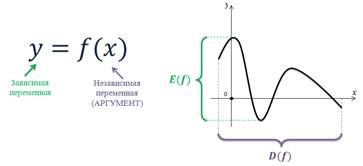
При этом букву x называют независимой переменной (или аргументом), а букву y — зависимой переменной. Число, которое подставляется вместо x, называется значением переменной (или значением аргумента), а число y, которому оно соответствует, называется значением функции.
График функции — множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Свойства функции:
1) Что такое область определения функции? Область определения функции (О.О.Ф) — это множество всех значений переменной x, которые имеют соответствующие им значения функции.
Редакция репетитора по математике: область определения — множество значений переменной x, у которых можно найти y.
Обозначения области определения Для обозначения области определения используются следующие знаки: 
Как найти область определения по графику? Область определения — это промежутки на оси Ох, над которыми (или под которыми) имеются части графика.
2) Что такое область значений функции? Областью значений функции (О.З.Ф) называется множество всех ее значений.
Редакция репетитора по математике:областью значений функции можно назвать часть оси ОY, состоящую из игреков, у которых есть соответствующие им иксы.
Как найти область значений по графику?: область значений функции — это промежутки на оси OY, слева или справа от которых (в горизонтальной полоске) находятся части графика.
3) Возрастание и убывание функции.
Какая функция называется возрастающей?Функция 
называется возрастающей, если для любой пары значений аргументов 
и 
из неравенства 
следует неравенство 
.
Редакция репетитора по математике: Функцию можно назвать возрастающей на промежутке, если, большему из любых двух взятых из него чисел всегда соответствует большее значение функции. Для графика это будет означать то, что при движении по нему карандашом слева направо карандаш будет подниматься вверх.
Какая функция называется убывающей? Функция называется убывающей, если для любой пары значений аргументов и из неравенства следует неравенство 
f (x_2)’ style=’vertical-align:-30%’ alt=’f (x_1)>f (x_2)’ />.
Редакция репетитора по математике: Функцию можно назвать убывающей на промежутке, если большему из любых двух взятых из него чисел всегда соответствует меньшее значение функции. Для графика это будет означать, что при движении по нему карандашом слева направо карандаш будет опускаться вниз.
Можно предложить еще один вариант этого определения: функция называется возрастающей на промежутке, если знак которым связаны любые два числа ее области определения, противоположен тому, которым связаны соответствующие им значения функции.
4) Промежутки знакопостоянства — промежутки, на которых функция имеет постоянный знак (положительный или отрицательный).
Пояснения репетитора по математике: Промежуток положительного знака — это множество значений переменной x, у которых соответствующие значения функции больше нуля (y>0 ).
Как найти все такие промежутки по графику? Определите промежутки оси ОХ, у которых соответствующие кусочки графика выше оси Ох.
Как их найти без графика? составьте и решите неравенство f (x)>0
Оформление: 
o ‘ style=’vertical-align:-5%’ alt=’y>o ‘ />, если 
Промежуток отрицательного знака — это множество тех значений переменной х, у которых соответствующие значения функции меньше нуля (y
Функция
1. Понятие функции
2. Cвойства функций
2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1 ) x2, f(x1) ) f(x2).
область определения (-∞,∞)
область значений (0; ∞)
общего вида
возрастает на (-∞,∞), если a>1;
убывает на (-∞,∞), если 0 непериодическая
Логарифмическая функция
у = log ₐ x (a>0 a≠1)
область определения (0,∞)
область значений (-∞; ∞)
общего вида
возрастает на (0,∞), если a>1;
убывает на (0,∞), 0 непериодическая
Тригонометрические функции
y = sin x
область определения (-∞; ∞)
область значений [-1; 1]
нечетная
возрастает на [-π/2 + 2πn, π/2 + 2πn];
убывает на [π/2 + 2πn, 3π/2 + 2πn], nϵZ;
период Т=2π
y = cos x
область определения (-∞; ∞)
область значений [-1; 1]
четная
возрастает на [-π + 2πn, 2πn];
убывает на [2πn, π + 2πn], nϵZ;
период Т=2π
y = tg x
область определения
(-π/2 + πn, π/2 + πn) nϵZ;
область значений (-∞; ∞)
нечетная
возрастает на (-π/2 + πn, π/2 + πn) nϵZ;
период Т=π
y = ctg x
область определения
(πn, π + πn) nϵZ;
область значений (-∞; ∞)
нечетная
убывает на (πn, π + πn) nϵZ;
период Т=π
y = arcsin x
область определения [-1; 1]
область значений [-π/2; π/2]
нечетная
возрастает на [-1; 1]
y = arccos x
область определения [-1; 1]
область значений [0; π]
функция центрально-симметрична относительно точки (0; π/2)
убывает на [-1; 1]
y = arctg x
область определения (-∞; ∞)
область значений [-π/2; π/2]
нечетная
возрастает на (-∞; ∞)
y = arcctg x
область определения (-∞; ∞)
область значений [0; π]
ни четная, ни нечетная
убывает на (-∞; ∞)
Свойства функций
Урок 2. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Свойства функций»
На прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились находить область определения и область значений функции.
· промежутки знакопостоянства функции;
· промежутки монотонности функции.
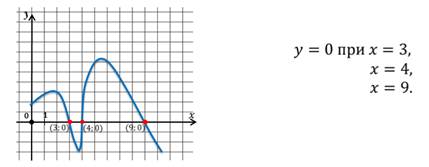
Нулями функции называют такие значения аргумента, при которых функция равна нулю.
В данном случае функция задана графически и мы определили нули функции по графику. Так же нули функции можно находить по формуле, с помощью которой задана функция.
Решив уравнение, мы найдём те значения х, при которых функция равна нулю.
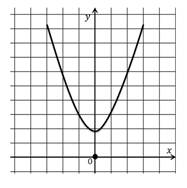
Стоит обратить внимание на то, что не каждая функция имеет нули.
График не пересекает ось икс ни в одной точке.
Промежутки знакопостоянства функции
Функция принимает положительные значения:
И отрицательные значения:
Запишите промежутки знакопостоянства функции:
Положительные и отрицательные значения функции:
Промежутки монотонности функции
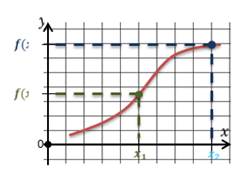
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Опишем свойства функции:
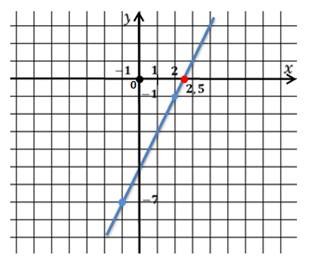
Графиком является прямая, поэтому для построения достаточно двух точек:
Найдём значения функции:
Областью определения и областью значений будет множество всех действительных чисел. Ведь х и у могут быть любыми числами.