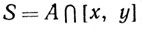Что такое связное подмножество
Что такое связное подмножество
Связные множества
2.45. Определение. Множество Е в метрическом пространстве X называется связным, если не существует двух открытых множеств А и В пространства X, таких, что пересечение А∩В пусто, пересечения А∩Е и В∩Е не пусты и Е⊂А∪В.
Это определение похоже на определение компактности, поскольку на самом деле оно не зависит от объемлющего пространства X, т. е. при замене слова «связное» словами «связное относительно X» в предыдущем абзаце выполняется следующее утверждение: Е связно относительно X в том и только в том случае, когда Е связно относительно Е.
Таким образом, имеет смысл говорить о связных пространствах (ср. с замечаниями, следующими за формулировкой теоремы 2.33): пространство связно, если оно не является объединением двух непустых непересекающихся открытых множеств.
Первая часть утверждения, набранного выше курсивом, почти тривиальна: если Е не является связным относительно X, то существуют множества А и В, обладающие свойствами, указанными в определении, ичрассмотрение множеств А∩Е и В∩Е показывает, что Е не связно относительно Е (ср. с теоремой 2.30). Обратное вытекает из следующего результата.
Доказательство. Каждой точке р∈G соответствует число δp>0, такое, что из соотношений q∈E, d(p, q) 0, такое, что из соотношений р∈Е, d(p, q) 1 связно тогда и только тогда, когда Е обладает следующим свойством: если х∈Е, у∈Е и x 0, то определение 2.45 показывает, что Е не связно.
К какому из этих типов принадлежит множество Е, зависит от того, конечны или нет inf E и sup E и принадлежат ли они множеству Е.
Столь же простой характеристики связных множеств на плоскости, например, не существует.
Связное множество
Смотреть что такое «Связное множество» в других словарях:
Связное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Связное множество — множество, любые две точки которого можно соединить непрерывной кривой, принадлежащей этому же множеству … Начала современного естествознания
СВЯЗНОЕ МНОЖЕСТВО — подмножество объемлющего множества, в к ром определено понятие связности и в смысле к рого само подмножество связно. Напр., С. м. пространства действительных чисел являются выпуклые множества и только они; С. м. графа является такое множество, в… … Математическая энциклопедия
Множество мандельброта — В математике множество Мандельброта это фрактал, определённый как множество точек на комплексной плоскости, для которых итеративная последовательность … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Связное пространство — Множество A связно, а … Википедия
Связное двоеточие — Связное двоеточие, или двоеточие Александрова наиболее простой содержательный пример нехаусдорфова топологического пространства в общей топологии. Содержание 1 Определение 2 Описание 3 Свойс … Википедия
Массивное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Несвязное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Что такое связное подмножество
Пространство называется связным, если оно не является объединением двух непересекающихся открытых непустых множеств. Когда пространство несвязно, два открытых множества, объединением которых оно является, будут также замкнутыми, так: что можно сказать, что пространство связно, если оно не является объединением двух непересекающихся замкнутых непустых множеств.
Пространство, состоящее из одной точки, связно; пространство, состоящее из конечного числа точек, большего 1, несвязно.
Множество С, содержащееся в пространстве 
называется связнымг если подпространство С связно.
Компонентой связности, или связной компонентой, точки 
из С называют наибольшую связную часть множества С, содержащую 
Легко показать, что:
объединение двух связных множеств, имеющих общую точку, есть связное множество;
непрерывный образ связного пространства есть связное пространство.
Связное компактное пространство (или множество) называется континуумом. Непрерывный образ континуума есть континуум.
Открытое связное множество называется областью.
Пусть А — подмножество пространства 
если СА несвязно, то мы оворим, что А разбивает 
или что А есть купюра Е.
Связное множество
Курсив обозначает ссылку на этот словарь
Литература
Полезное
Смотреть что такое «Связное множество» в других словарях:
Связное множество — множество, любые две точки которого можно соединить непрерывной кривой, принадлежащей этому же множеству … Начала современного естествознания
Связное множество — (математическое) точечное множество, состоящее как бы из одного куска, т. е. такое, что при любом его разбиении на два непресекающихся непустых подмножества одно из них содержит точку, предельную для другого (см. Предельная точка). На… … Большая советская энциклопедия
СВЯЗНОЕ МНОЖЕСТВО — подмножество объемлющего множества, в к ром определено понятие связности и в смысле к рого само подмножество связно. Напр., С. м. пространства действительных чисел являются выпуклые множества и только они; С. м. графа является такое множество, в… … Математическая энциклопедия
Множество мандельброта — В математике множество Мандельброта это фрактал, определённый как множество точек на комплексной плоскости, для которых итеративная последовательность … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Связное пространство — Множество A связно, а … Википедия
Связное двоеточие — Связное двоеточие, или двоеточие Александрова наиболее простой содержательный пример нехаусдорфова топологического пространства в общей топологии. Содержание 1 Определение 2 Описание 3 Свойс … Википедия
Массивное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Несвязное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Связное пространство
Связное пространство — топологическое пространство, которое невозможно разбить на два непустых непересекающихся открытых подмножества.
Содержание
Связанные определения
Свойства
Примеры
Вариации и обобщения
Полезное
Смотреть что такое «Связное пространство» в других словарях:
СВЯЗНОЕ ПРОСТРАНСТВО — топологическое пространство, к рое нельзя представить в виде суммы двух отделенных друг от друга частей или, более строго, непустых непересекающихся открыто замкнутых подмножеств. Пространство связно тогда и только тогда, когда каждая непрерывная … Математическая энциклопедия
Линейно связное пространство — Линейно связное пространство это топологическое пространство, в котором любые две точки можно соединить непрерывной кривой. Содержание 1 Определения 2 Связанные определения 3 … Википедия
ЛОКАЛЬНО СВЯЗНОЕ ПРОСТРАНСТВО — топологическое пространство X, в к ром для любой точки хи любой ее окрестности О х имеется меньшая связная окрестность Ux. Всякое открытое подмножество Л. с. п. локально связно. Всякая компонента связности Л. с. п. открыто замкнута. Пространство… … Математическая энциклопедия
ЛОКАЛЬНО ЛИНЕЙНО СВЯЗНОЕ ПРОСТРАНСТВО — топологическое Пространство X, В к рол ДЛЯ любой точки и любой ее окрестности О х существует меньшая окрестность такая, что для любых двух точек существует непрерывное отображение единичного отрезка I=[0, 1] в окрестность Всякое Л. л. с. п.… … Математическая энциклопедия
ЛИНЕЙНО СВЯЗНОЕ ПРОСТРАНСТВО — топологическое пространство, в к ром любые две точки можно соединить непрерывным образом простой дуги, т. е. пространство X, для любых двух точек х 0 и x1 к рого существует такое непрерывное отображение единичного отрезка I = [0, 1], что f(0) =… … Математическая энциклопедия
Связное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Связное двоеточие — Связное двоеточие, или двоеточие Александрова наиболее простой содержательный пример нехаусдорфова топологического пространства в общей топологии. Содержание 1 Определение 2 Описание 3 Свойс … Википедия
ВПОЛНЕ НЕСВЯЗНОЕ ПРОСТРАНСТВО — пространство, в к ро, м всякое подмножество, содержащее более одной точки, несвязно. Равносильное условие: компонента связности любой, точки пространства состоит из одной этой точки. Топологич. произведение и топологич. сумма В. н. п., равно как… … Математическая энциклопедия
ПУТЕЙ ПРОСТРАНСТВО — пространство Ерасслоения ( Е, р, X), называемое расслоением путей, где X линейно связное пространство с отмеченной точкой *, Е множество путей в X, начинающихся в *, р отображение, сопоставляющее каждому пути его концевую точку; при этом… … Математическая энциклопедия