Что такое связные графы

Теория графов — связность

Возможен ли переход графа из одной вершины в другую, определяется тем, как граф связан. Связность является основной концепцией в теории графов. Связность определяет, подключен ли график или нет. Он имеет подтемы, основанные на ребре и вершине, известные как связность ребер и вершин. Давайте обсудим их подробно.

связь

Пример 1

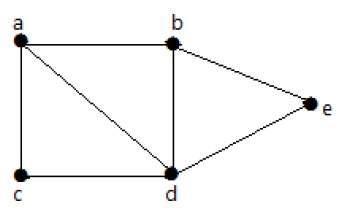
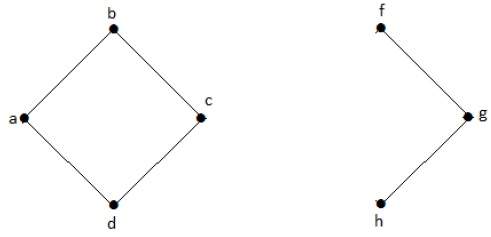
На следующем графике можно перейти от одной вершины к любой другой вершине. Например, можно перейти от вершины «а» к вершине «е», используя путь «ab-e».

Пример 2

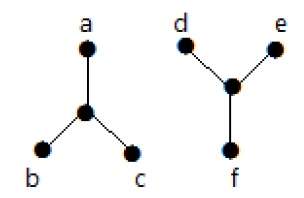
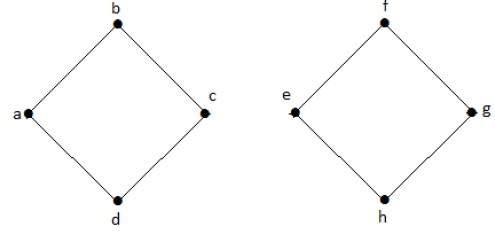
В следующем примере переход от вершины ‘a’ к вершине ‘f’ невозможен, поскольку между ними нет прямого или косвенного пути. Следовательно, это несвязный граф.

Cut Vertex

Пусть ‘G’ связный граф. Вершина V ∈ G называется разрезанной вершиной из «G», если «G-V» (исключить «V» из «G») приводит к несвязному графу. Удаление вырезанной вершины из графа разбивает ее на два или более графа.

Примечание. Удаление обрезанной вершины может привести к отключению графа.

Связный граф ‘G’ может иметь не более (n – 2) вершин среза.

пример

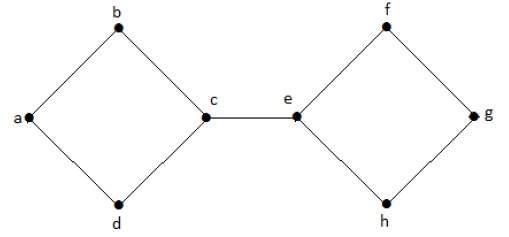
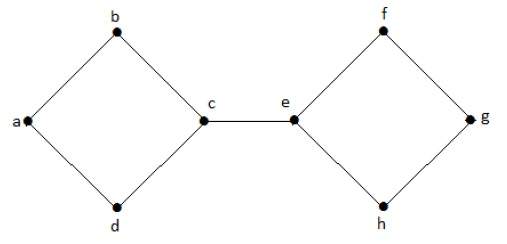
На следующем графике вершины ‘e’ и ‘c’ являются вырезанными вершинами.

Удалив «е» или «с», граф станет несвязным графом.

Без ‘g’ нет пути между вершиной ‘c’ и вершиной ‘h’ и многими другими. Следовательно, это несвязный граф с разрезанной вершиной в виде «е». Точно так же ‘c’ также является вершиной разреза для приведенного выше графа.

Cut Edge (Мост)

Пусть ‘G’ связный граф. Ребро «e» ∈ G называется отрезанным ребром, если «G-e» приводит к несвязному графу.

Если удаление ребра в графе приводит к двум или более графам, то это ребро называется Cut Edge.

пример

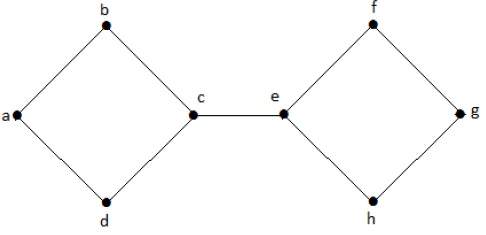
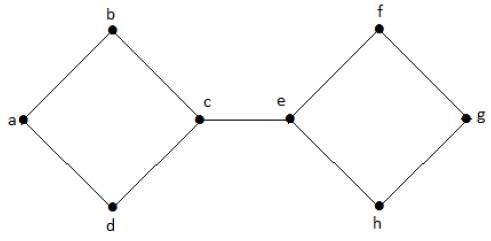
На следующем графике край обрезки равен [(c, e)]

Удаляя ребро (c, e) из графа, он становится несвязным графом.

В приведенном выше графике удаление ребра (c, e) разбивает граф на два, что является ничем иным, как несвязным графом. Следовательно, ребро (c, e) является отрезанным ребром графа.

Примечание. Пусть «G» — связный граф с «n» вершинами, тогда

отрезок e ∈ G тогда и только тогда, когда ребро «e» не является частью какого-либо цикла в G.

Максимально возможное количество режущих кромок равно n-1.

всякий раз, когда существуют ребра среза, вершины среза также существуют, потому что по крайней мере одна вершина среза является вершиной среза.

если вершина разреза существует, то край разреза может существовать или не существовать.

отрезок e ∈ G тогда и только тогда, когда ребро «e» не является частью какого-либо цикла в G.

Максимально возможное количество режущих кромок равно n-1.

всякий раз, когда существуют ребра среза, вершины среза также существуют, потому что по крайней мере одна вершина среза является вершиной среза.

Источник

Связный граф

Связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует как минимум один путь.

Содержание

Примеры применения

Прямым применением теории графов является теория сетей — и её приложение — теория электронных сетей. Например, все компьютеры, включенные в сеть Интернет, образуют связный граф, и хотя отдельная пара компьютеров может быть не соединена напрямую (в формулировке для графов — не быть соединены ребром), от каждого компьютера можно передать информацию к любому другому (есть путь из любой вершины графа в любую другую).

Связность для ориентированных графов

В ориентированных графах различают несколько понятий связности.

Ориентированный граф называется сильно-связным, если в нём существует (ориентированный) путь из любой вершины в любую другую, или, что эквивалентно, граф содержит ровно одну сильно связную компоненту.

Ориентированный граф называется слабо-связным, если является связным неориентированный граф, полученный из него заменой ориентированных рёбер неориентированными.

Некоторые критерии связности

Здесь приведены некоторые критериальные (эквивалентные) определения связного графа:
Граф называется односвязным (связным), если:

См. также

Полезное

Смотреть что такое «Связный граф» в других словарях:

связный граф — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN connected graph … Справочник технического переводчика

Связный граф — 8. Связный граф По ГОСТ 19880 74 Источник: ГОСТ 23070 78: Анализ и оптимизация на ЭВМ радиоэлектронных схем. Термины и определения … Словарь-справочник терминов нормативно-технической документации

граф — Графическое изображение электрической цепи, в котором ветви электрической цепи представлены отрезками, называемыми ветвями графа, а узлы электрической цепи — точками, называемыми узлами графа. [ГОСТ Р 52002 2003] граф Основное понятие и… … Справочник технического переводчика

Граф — [graph] основное понятие и объект изучения теории графов, математически определяется двояко. С одной стороны как совокупность двух множеств: множества элементов x Î X и множества соответствий, отношений между этими элементами t Î T. С другой… … Экономико-математический словарь

Граф (математика) — У этого термина существуют и другие значения, см. Граф (значения). Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность непустого множества вершин и множества пар… … Википедия

Граф (теория графов) — Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи как дуги, или рёбра. Для… … Википедия

Связный список — В информатике, связный список базовая динамическая структура данных, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки («связки») на следующий и/или предыдущий узел списка.[1] Принципиальным… … Википедия

Вершина (граф) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник

Лекция 13. Графы

4.2. Связность

Маршруты

Определение 4.9. Последовательность из ребер графа (не обязательно различных) называется маршрутом длины , если любые два рядом стоящие в этой последовательности ребра смежные. Кроме того, если эти два рядом стоящие ребра ориентированные, то в инцидентную им вершину ребро, стоящее слева, должно входить, а ребро, стоящее справа, из нее выходить.

только из одной вершины графа.

Связные компоненты

Пусть задан неориентированный граф. Граф называется связным, если любые две несовпадающие вершины графа соединены маршрутом. Очевидно, что для связности графа необходимо и достаточно, чтобы произвольная фиксированная вершина графа соединялась маршрутом с каждой из оставшихся вершин этого графа.

Отношение связности рефлексивно (вершина всегда связана сама с собой), симметрично (из связности вершины с вершиной следует связность вершины с вершиной ) и транзитивно (если вершины , и вершины , связаны, то связаны и вершины ,). Таким образом, отношение связности для вершин есть отношение эквивалентности. Поэтому существует такое разбиение множества вершин графа на попарно непересекающиеся подмножества (классы эквивалентности), что все вершины в каждом подмножестве связаны, а вершины из различных подмножеств не связаны. Каждое такое подмножество вершин графа вместе с ребрами, инцидентными этим вершинам, образует связный подграф. Следовательно, неориентированный граф представим единственным образом в виде объединения непересекающихся связных подграфов. Эти подграфы называют связными компонентами рассматриваемого графа. Связный граф является своей единственной компонентой связности. На рис.4.21 изображен граф, который имеет три компоненты связности.

Теперь обратимся к ориентированному графу. Если в орграфе существует маршрут, связывающий вершины и , то говорят, что вершина достижима из вершины . Любая вершина считается достижимой из себя самой. Вершина орграфа называется источником, если из нее достижима любая вершина орграфа.

Связность ориентированных графов определяется в принципе так же, как и неориентированных, те есть без учета направления дуг. Специфичным для орграфа (или смешанного графа) является понятие сильной связности.

Орграф называется сильным (или сильносвязным), если любые две его вершины достижимы друг из друга. Орграф называется односторонним (или одностороннесвязным), если для любой пары его вершин, по меньшей мере, одна из них достижима из другой.

Рис.4.22 Рис.4.22 Рис.4.22

В некоторых задачах существенно требование сильной связности графа. Например, граф, представляющий план города с односторонним движением по некоторым улицам, должен быть сильно связанным, так как, в противном случае, нашлись бы вершины (площади и перекрестки), между которыми нельзя было бы проехать по городу без нарушения правил движения.

Маршрут, содержащий все вершины орграфа, называется остовным.

Теорема 4.5. Орграф является сильным тогда и только тогда, когда в нем есть остовный контур, является односторонним тогда и только тогда, когда в нем есть остовный путь.

Отношение взаимной достижимости вершин орграфа рефлексивно, симметрично и транзитивно. Как отношение эквивалентности оно разбивает множество вершин орграфа на классы эквивалентности, объединяя в один класс все вершины, достижимые друг из друга. Вершины, входящие в такие классы, вместе с дугами, им инцидентными, обе концевые вершины которых принадлежат этому же классу, образуют подграфы, называемые сильными (или сильносвязнными) компонентами орграфа.

Орграф называется несвязным, когда его неориентированный дубликат не является связным графом.

Орграф, изображенный на рис. 4.25, имеет четыре сильные компоненты с множествами вершин , , , . В орграфе могут быть дуги, не входящие ни в одну из его сильных компонент, например, дуги , , и у орграфа на рис. 4. 25.

Вершинная связность и реберная связность

Сопоставляя, например, полный граф шестого порядка и его любой связный суграф, интуитивно ясно, что сам полный граф «сильнее» связан, чем его суграф. Далее речь пойдет о понятиях, характеризующих степень связности графа.

Рассмотрим граф, вершины которого соответствуют неким технологическим объектам, а ребра показывают, какие объекты могут взаимодействовать либо непосредственно друг с другом, либо опосредованно через другие объекты. Технологическая система, представленная этим графом, считается функционирующей, если каждая пара ее объектов связана между собой. В этом случае система должна иметь связный граф. Важной характеристикой системы является ее надежность (живучесть), под которой обычно понимается способность системы функционировать при выходе из строя одного или нескольких объектов и (или) нарушения связи между некоторыми из них. Очевидно, что менее надежной следует считать ту систему, которая перестает функционировать при выходе из строя меньшего количества ее элементов. Оказывается, оценить степень надежности такой системы могут помочь те понятия, о которых упоминалось чуть выше и которые сейчас будут определены.

Определение 4.10. Числом вершинной связности (или просто числом связности) графа называется число, равное наименьшему числу вершин, удаление которых приводит к несвязному или одновершинному графу.

Граф , представленный на рис. 4.26, связен, но он перестает быть связным, если удалить вершину 4. Поэтому .

Можно нарушить связность графа, удаляя некоторые его ребра (дуги). У графа (рис. 4.26) для этого придется удалить не менее трех ребер. Например, граф распадается на две компоненты после удаления ребер 4&5, 4&6, 4&7.

Определение 4.11. Числом реберной связности графа называется число, равное наименьшему числу ребер, удаление которых приводит к несвязному графу. Число реберной связности одновершинного графа полагается равным нулю.

Выше мы показали, что для графа (рис. 4.26) .

Ребро графа называется мостом, если его удаление увеличивает число компонент связности графа.

Возвращаясь к технологической системе, речь о которой шла вначале, отметим, что число вершинной связности и число реберной связности ее графа отражают чувствительность системы к повреждениям, а точки сочленения и мосты графа системы указывают на наиболее уязвимые места системы.

Граф называется неразделимым, если он связный и не имеет точек сочленения. Граф, имеющий хотя бы одну точку сочленения, является разделимым и называется сепарабельным. Он разбивается на блоки, каждый из которых представляет собой максимальный неразделимый подграф.

На рис. 4.28 показаны блоки , , графа на рис. 4.26.

Если есть минимальная степень вершин графа , то очевидно, что , поскольку удаление всех ребер, инцидентных данной вершине, приводит к увеличению числа компонент связности графа.

Теорема 4.6. Для любого графа справедливы неравенства:

.

Граф называется k-связным, если , реберно— k-связным, если .

Граф , изображенный на рис. 4.26, 1-связен и реберно-3-связен.

Источник

3.04.1. Связные графы и расстояние в графах. Маршруты в графах. Связные графы

Такая, что — ребро в графе G, соединяющее Vi C Vi+1 Называется . Вершина V1 при этом называется началом маршрута, а Vn+1 – концом маршрута. Число рёбер N в маршруте называется Длиной маршрута. Во взвешенном графе за длину маршрута принимается сумма весов входящих в маршрут рёбер.

В простом графе, когда смежные вершины соединены только одним ребром, для задания маршрута достаточно указать только последовательность вершин ( разумеется, любые две соседние вершины в этой последовательности должны быть смежными). В этом случае (V1, V N+1) – маршрут обозначается: (V1, V2, V3, …, Vn+1).

В маршруте вершины и рёбра могут повторяться. Если в маршруте все рёбра различны, то он называется Цепью. Если кроме того в цепи различны и все вершины (кроме, может быть, первой и последней), то такой маршрут называется Простой цепью.

Минимальная из длин всех циклов графа называется Охватом графа.

Граф G называется Связным, если в нем для любых двух вершин U и υ существует (U,υ)-маршрут.

В ориентированных графах рассматриваются ориентированные маршруты, в которых для любой пары соседних вершин υi и υi+1 существует дуга (υi, υi+1) (υi – начало дуги, υi+1 – конец). Другими словами – это маршруты, по которым можно передвигаться от начала маршрута к концу с соблюдением ориентации (стрелок).

Легко видеть, что всякий (U, υ)–маршрут содержит (U, υ)–цепь. Для того, что бы её получить, достаточно в маршруте исключить дублирование участков, которые проходятся несколько раз. Кроме того, если из (U, υ)–цепи удалить все промежуточные циклические участки, то получим простую (U, υ)–цепь.

Таким образом, можно дать эквивалентное определение связности: граф называется связным, если в нём любую пару вершин U и υ можно соединить простой (U, υ)–цепью.

Для связных графов вводиться также количественная характеристика их связности. Связностью Графа G называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу. Так, например, полный граф KN имеет связность N-1; простая цепь Pn имеет связность 1; простой цикл СN имеет связность 2; колесо Wn имеет связность 3.

Наименьшее число рёбер графа G, удаление которых приводит к несвязному подграфу, называется Ребёрной связностью графа G.

Компоненты связности. Связность графа и его дополнения

Максимальные связные подграфы графа G называются его Компонентами связности. Здесь “максимальные” означает: не содержатся в других подграфах с большим числом элементов.

На множестве вершин V(G) определим бинарное отношение. Положим V

U, если в G Существует (V, U)–маршрут. Легко видеть, что это отношение является отношением эквивалентности, причем V

U тогда и только тогда, когда вершины V и U содержатся в одной и той же компоненте связности. Таким образом, совокупность компонент связности есть разбиение данного графа (объединение компонент дает весь граф; различные компоненты связности не пересекаются).

Граф называется Графом достижимости графа G (или Транзитивным замыканием графа G), если V() = V(G) и в графе вершины V и U соединены ребром тогда и только тогда, когда в G существует (U, υ)–маршрут. Другими словами, в графе V и U смежны, если V

U В графе G (в смысле отношения эквивалентности, введенного выше).

Понятно, что граф G связен в том и только том случае, когда =Kn – полный граф. В случае же, когда G не является связным, является объединением нескольких полных подграфов, которые являются его компонентами связности.

Теорема. Всякий граф или его дополнение является связным.

Доказательство. Предположим, что G – не связный граф, и докажем, что тогда его дополнение Есть связный граф. Действительно, пусть A – множество вершин какой-либо компоненты связности графа G, а B=V(G)\A – остальные вершины. Тогда в графе всякая вершина AÎA соединена ребром с каждой вершиной BÎB. Пусть Ai, Aj Î A, тогда (Ai, b, aj) – маршрут, соединяющий Ai с Aj (здесь B –любая вершина из B). Аналогично, если Bi, bj Î B, то (Bi, a, bj) – маршрут соединяющий Bi с Bj, (A – любая вершина из A). Таким образом, для любых двух вершин в Существует соединяющий их маршрут (длины не более 2), что и требовалось доказать.

Источник