Что такое валидный процент
Валидность
Добавлено в закладки: 0
Валидность – это
1) мера соответствия, которая показывает насколько соответствуют поставленным задачам полученные результаты и разработанная методика исследования;
2) фундаментальное понятие в экспериментальной психологии и психодиагностике. Различают такие типы валидности: валидность по содержанию, конструктивная валидность, прогностическая валидность, валидность по критерию. Безупречную валидность имеет только теоретический безупречный эксперимент: эксперимент, при котором получаемый эффект вызывает независимую переменную, соответствует полностью реальности, а его итоги поддаются без дополнительных ограничений обобщению.
Как в статистике, так и в психологии, валидное измерение — такое измерение, которое измеряет то, что оно обязано измерять (эта узкая трактовка “валидности” – наиболее популярная, она по факту соответствует понятию “конструктная валидность”). То есть, например, при валидном измерении интеллекта измеряют именно интеллект, а не что-то другое. Безупречный эксперимент (возможный только в теории) будет иметь безупречную валидность: он точно будет показывать, что экспериментальный эффект вызван изменением независимой переменной, он будет соответствовать полностью реальности, его итоги можно без ограничений обобщить.
Когда говорят о степени валидности, рассматривают то, насколько итоги исследования соответствуют поставленным задачам (но при этом валидность не измеряется в каких-нибудь условных единицах).
Важная особенность валидности – её невозможно единожды установить и использовать это доказательство в качестве финального аргумента “за” качество определенной методики или эксперимента. Валидность нужно постоянно обосновывать новыми данными, в независимых исследованиях перепроверять.
Способы установления валидности методики

Существуют три главных метода установления валидности методики.
I. Оценка содержательной валидности
Содержательная валидность – степень соответствия содержания заданий методики реальной деятельности, в которой проявляют свойство, измеряемое в методике. Частным случаем содержательной валидности является так называемая очевидная (фейс или лицевая) валидность – степень соответствия методики ожиданиям оцениваемых. Для большей части методик считают важным, чтобы для участника оценки очевидна связь меж содержанием процедуры оценки и реальной деятельностью, которая является объектом оценки (семейная, профессиональная, учебная и так далее.).
II. Оценка конструктной валидности
Конструктная валидность – степень обоснованности того, что методика измеряет действительно заданные и при этом обоснованные научно конструкты. Есть, как минимум, две стратегии установления конструктной валидности.
Подход первый — «конвергентная валидизация» — проверка ожидаемой связи итогов конкретной методики с показателями прочих методик, которые измеряют сходные характеристики. К примеру, если для измерения какой-нибудь черты есть несколько методик, было бы целесообразным провести эксперименты по хотя бы двум, и тогда при выявлении высокой позитивной корреляции их итогов меж собой можно говорить о валидности. Главная цель конвергентной валидизации — определение того, будут ли оценки теста варьироваться соответственно с ожиданиями.
Подход второй — «дивергентная валидизация». Проверка валидности тут заключается в том, что тест не может измерять никакой черты, с которой он и не должен быть связан теоретически.
III. Оценка критериальной валидности

Одним из типов критериальной валидности является так называемая “прогностическая” валидность. Этот тип валидности применяется, когда методика призывается давать определенный прогноз поведения человека. Соответственно, когда прогноз с течением времени оправдывается, это говорит о том, что методика является валидной прогностически.
Профессиональные разработчики методик должны обосновывать все перечисленные типы валидности и проводить постоянный сбор свидетельств в пользу валидности их инструментов.
Типы валидности
В разных источниках упоминают различные названия, что может создать определенную путаницу. В экспериментальной психологии ключевые понятия:
Для организационной психологии и психодиагностики более традиционной является классификация из трех главных типов валидности:
Мы коротко рассмотрели валидность: типы и способы установления. Оставляйте свои комментарии или дополнения к материалу.
2.3. Вероятности и частоты
2.3.1 Вероятности и частоты в SPSS
Пример 2.3(1) Соотношение данных в генеральной совокупности и выборке. В файле IntroProb.sav содержатся модельные данные о частоте выраженности различных типов темперамента, полученные в результате проведения опроса по методике Айзенка. Таблица данных состоит из единственной переменной, названной introversion, содержащей данные о выраженности экстраверсии или интроверсии испытуемых (три градации переменной: 1 — интроверт, 2 — экстраверт, 3 — неопределенный тип (так называемый амбиверт)). Поскольку амбиверт не является промежуточным между экстравертом и интровертом типом, то шкалу можно считать номинативной. Таблица содержит очень большое количество измерений этих двух параметров (426 679), статистика соответствует данным, накопленным на сайте http://psyline.retter.ru/auzeng/st_e.php (по состоянию на май 2016 года).
Будем в рамках этого примера рассматривать данные как исчерпывающие генеральную совокупность. Скажем, нас интересует такая генеральная совокупность, как население города, в котором живет 426 679 человек. Такие полные данные о генеральной совокупности обычно либо не существуют вообще, либо засекречены. Допустим, что это секретная база, собранная сотрудниками спецслужб. В таком случае мы можем практически точно определить вероятность событий типа «случайный житель города — экстраверт» или «случайный житель города — интроверт». Для этого надо рассчитать относительную частоту появления того ли иного типа личности в нашей условной генеральной совокупности. Чтобы сделать это, зайдем в меню Анализ — Описательные статистики — Частоты (Analyze — Descriptive statistics — Frequencies). Также, для получения гистограммы, в дополнительном меню «Диаграммы» (Charts) следует выбрать пункт Гистограммы (Histogrames). В качестве анализируемой переменной укажем Introversion. В результате получим таблицу 2.3(2).
Таблица 2.3(2). Распределение типов личности в условной «генеральной совокупности»
| Интроверсия/экстраверсия | |||||
| Частота | Проценты | Валидный процент | Накопленный процент | ||
| Валидные | introvert | 203 423 | 47.7 | 47.7 | 47.7 |
| extravert | 184 524 | 43.2 | 43.2 | 90.9 | |
| ambivert | 38 732 | 9.1 | 9.1 | 100.0 | |
| Всего | 426 679 | 100.0 | 100.0 | ||
Из нее следует, что вероятность интроверсии составляет 0.477 (47.7%), экстраверсии — 0.432, а амбиверсии — 0.091.
Полученная гистограмма (соответствующая таблице) изображена на рис. 2.3(3). 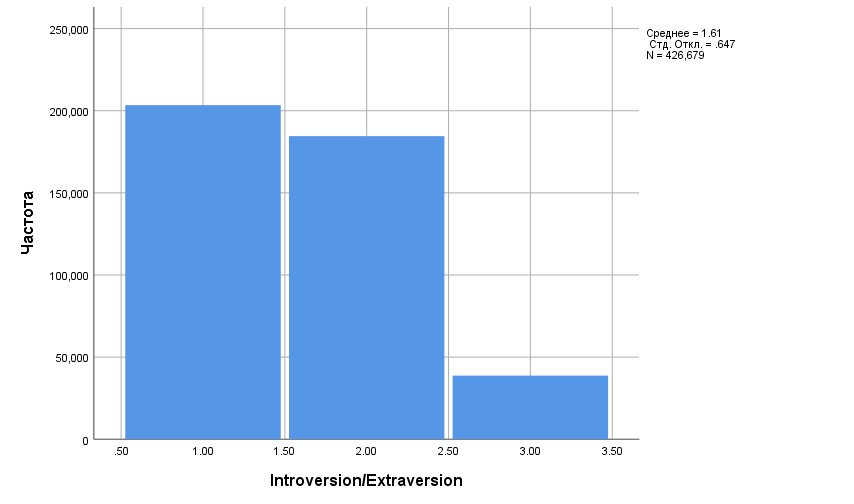
Упражнение 2.3(4). В файле TempProb.sav содержатся данные о выраженности темперамента у жителей того же города. В переменной temp приведена принадлежность жителей к одному из четырех типов темперамента: 1 — холерик, 2 — сангвиник, 3 — флегматик, 4 — меланхолик или 5 — к неопределенному типу. Исходя из положения, что эти данные соответствуют генеральной совокупности, рассчитайте вероятности того, что случайный житель будет обладать тем или иным типом темперамента.
Пример 2.3(5). Смоделируем ситуацию выборочной оценки распределения вероятностей в генеральной совокупности. Допустим, в городе, о котором шла речь в Примере 2.3(1), проводится исследование, направленное на оценку соотношения интровертов и экстравертов. Исследование проводится неким институтом и этим проектом занимаются 10 исследователей. Каждый из исследователей тестирует 100 случайно отобранных жителей города. Таким образом, каждый из них получает выборку размером 100, а при объединении всех набранных данных можно получить большую выборку размером 1000. В файле IntroProbResearch.sav содержатся модельные данные такого исследования тысячи человек десятью исследователями. В первом столбце так же, как и в предыдущем примере, отмечена принадлежность испытуемых к интровертам, экстравертам или амбивертам, а во втором — ResearcherId — условный номер исследователя, который собрал эти данные (от 1 до 10). Сравним результаты, полученные отдельными исследователями, между собой и с данными из Примера 2.3(1) Для этого можно использовать функцию разбиения файла в SPSS: последовательно выбрать пункты меню Данные — Расщепить файл (Data — Split file) и в появившемся диалоговом окне выбрать пункт Организовать вывод по группам (Organize output by), а затем вставить в поле Группы образуются по: (Group based on: ) переменную ResearcherId и нажать кнопку OK. После этого SPSS будет проводить любой анализ отдельно для каждой из групп с разными номерами исследователей.
При повторении расчета частот значений переменной introversion, описанного в Примере 2.3(1), в этом случае мы получим 10 различных таблиц. При этом различия между данными, полученными различными исследователями, будут довольно заметны. Например, доли интровертов, экстравертов и амбивертов по данным исследователя номер 3 будут 0.55, 0.42 и 0.03, а если мы возьмем данные, полученные исследователем номер 10, то доли будут 0.5, 0.4 и 0.1 соответственно.
Упражнение 2.3(6). Соотнесите результаты, полученные каждым из 10 исследователей с данными «генеральной совокупности». Насколько они отличаются от данных, полученных в генеральной совокупности? Как будет соотноситься результат каждого из исследователя с «истинным» распределением типов личности в генеральной совокупности, если каждый исследователь обследует не 100, а только 10 жителей города? А если каждый сумеет обследовать 1000 жителей? В каком случае полученные данные будут более схожими с генеральной совокупностью?
Пример 2.3(7). Если мы объединим выборки, полученные 10 исследователями в одну большую «мета-выборку», то мы получим данные в общей сложности на 1000 случайных респондентов. Проведение частотного анализа соотношения типов личности в объединенной выборке даст результат, приведенный в таблице 2.3(8).
Таблица 2.3(8). Распределение типов личности в объединенной выборке (1000 человек)
| introversion | |||||
| Частота | Проценты | Валидный процент | Накопленный процент | ||
| Валидные | introvert | 494 | 49.4 | 49.4 | 49.4 |
| extravert | 423 | 42.3 | 42.3 | 91.7 | |
| ambivert | 83 | 8.3 | 8.3 | 100.0 | |
| Всего | 1 000 | 100.0 | 100.0 | ||
Как видно из таблицы, полученные частоты того или иного типа личности уже достаточно близки к полученным в генеральной совокупности, о чем свидетельствует и форма гистограммы общих данных (рис. 2.3(9)).
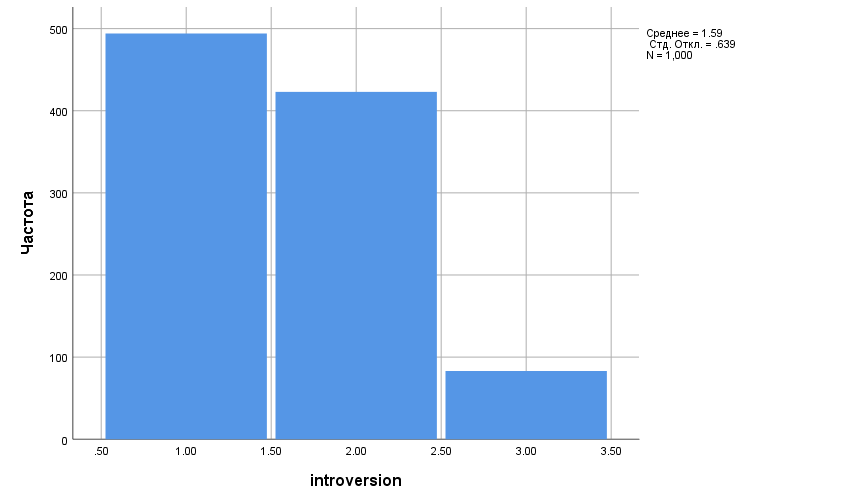
Данный пример наглядно демонстрирует, что недостаточный объем выборки может приводить к искажению оценки вероятности того или иного события (или значения параметра) в генеральной совокупности. В дальнейшем мы обсудим закон больших чисел, которые строго показывает, что увеличение выборки приводит к все более точной оценке «истинного» значения любого параметра в генеральной совокупности.
Пример 2.3(10) Вызовите файл IntroProb.sav и попробуйте самостоятельно смоделировать исследование, в которое включено 100 случайных жителей города.
Упражнение 2.3(11). Для отбора случайной выборки заданного размера в матрице данных в диалоговом окне отбора переменных Данные — Отобрать наблюдения (Data — Select Cases) надо выбрать вариант Случайная подвыборка (Random sample of cases) и, нажав кнопку Подвыборка (Sample), указать Точно k наблюдение из первых n наблюдений (Exactly k cases from the first n cases), где k — размер подвыборки (100 для этого упражнения), а n — размер всей выборки (426 679 в нашем примере). После этого SPSS случайным образом отберет k наблюдений и будет включать в анализ только их до тех пор, пока фильтр не будет изменен или отключен (вариант Все наблюдения (All cases) в диалоговом окне отбора наблюдений). Рассчитайте таблицу частот значений переменной introversion. Насколько полученные результаты соответствуют данным генеральной совокупности?
Упражнение 2.3(12). Повторите эту процедуру для 1000 случайно отобранных испытуемых. Проверьте, насколько ваш ответ на заданный выше вопрос соответствует полученному в этом случае результату. Повышается или понижается согласованность данных в генеральной совокупности и в выборке большего размера по сравнению с небольшой выборкой?
Пример 2.3(13). Рассмотрим ситуацию биномиального эксперимента, описанного в подпараграфе 2.2.4, в котором подбрасывают три монеты и считают количество выпавших гербов. Теоретические вероятности выпадения 0, 1, 2 и 3 в случае симметричной монеты равны 1/8, 3/8, 3/8 и 1/8 соответственно (см. 2.2.4). В файле 3FairCoins.sav приведены смоделированные данные эксперимента, в котором три монеты подбрасывают 1000 раз и каждый раз фиксируют количество гербов (единственный столбец — heads). Результаты расчета частоты появления каждого из возможных исходов представлены в таблице 2.3(14).
Таблица 2.3(14). Частота выпадения k гербов при подбрасывании трех монет
| Number of heads | |||||
| Частота | Проценты | Валидный процент | Накопленный процент | ||
| Валидные | 0.00 | 127 | 12.7 | 12.7 | 12.7 |
| 1.00 | 377 | 37.7 | 37.7 | 50.4 | |
| 2.00 | 375 | 37.5 | 37.5 | 87.9 | |
| 3.00 | 121 | 12.1 | 12.1 | 100.0 | |
| Всего | 1 000 | 100.0 | 100.0 | ||
Из таблицы видно, что относительная частота достаточно близка к рассчитанным выше теоретическим вероятностям.
Упражнение 2.3(15). В файле 3UnknownCoins.sav содержатся модельные результаты трех серий экспериментов, аналогичных описанному в предыдущем примере. Однако в одном из экспериментов использовались симметричные монеты, а в двух других искривленные так, что в одной серии более вероятным было выпадение герба, а в другой — выпадение цифры. Данные представлены в трех столбцах (heads1, heads2 и heads3). Порядок серий с симметричными и асимметричными монетами неизвестен. Мы предлагаем читателю самостоятельно рассчитать частоты выпадения того или иного числа гербов и определить, в какой переменной содержатся данные об эксперименте с симметричной монетой, а в каких — данные об искривленных в пользу орла или цифры монетах.
2.3.2 Вероятности и частоты в Jamovi
Пример 2.3(1)j Соотношение данных в генеральной совокупности и выборке. В файле IntroProb.sav содержатся модельные данные о частоте выраженности различных типов темперамента, полученные в результате проведения опроса по методике Айзенка. Таблица данных состоит из единственной переменной, названной introversion, содержащей данные о выраженности экстраверсии или интроверсии испытуемых (три градации переменной: 1 — интроверт, 2 — экстраверт, 3 — неопределенный тип (так называемый амбиверт)). Поскольку амбиверт не является промежуточным между экстравертом и интровертом типом, то шкалу можно считать номинативной. Таблица содержит очень большое количество измерений этих двух параметров (426 679), статистика соответствует данным, накопленным на сайте http://psyline.retter.ru/auzeng/st_e.php (по состоянию на май 2016 года).
Будем в рамках этого примера рассматривать данные как исчерпывающие генеральную совокупность. Скажем, нас интересует такая генеральная совокупность, как население города, в котором живет 426 679 человек. Такие полные данные о генеральной совокупности обычно либо не существуют вообще, либо засекречены. Допустим, что это секретная база, собранная сотрудниками спецслужб. В таком случае мы можем практически точно определить вероятность событий типа «случайный житель города — экстраверт» или «случайный житель города — интроверт». Для этого надо рассчитать относительную частоту появления того ли иного типа личности в нашей условной генеральной совокупности. Чтобы сделать это, зайдем в меню Exploration—Descriptives
Перетащим переменную introversion в окно Variables. В правом окне результатов появляется таблица, в которой выведены среднее значение, медиана, максимум и минимум.
Вопрос 1. Имеет ли смысл среднее значение для номинативной переменной?
Ответ. Не имеет.
Эту таблицу лучше убрать в данном случае. Для этого надо кликнуть надпись Statistics и убрать в выпавшем окне все галочки. Таблица исчезнет. Для того, чтобы была выведена нужная информация, вставьте галочку в окошко Frequency tables и, нажав на надпись Plots, проставить галочку в окошко Hystogram
В результате получим таблицу 2.3(2)j.
Таблица 2.3(2)j. Распределение типов личности в условной «генеральной совокупности»
Frequencies
| Levels | Counts | % of Total | Cumulative % | ||||
| introvert | 203423 | 47.7 % | 47.7 % | ||||
| extravert | 184524 | 43.2 % | 90.9 % | ||||
| ambivert | 38732 | 9.1 % | 100.0 % | ||||
Из нее следует, что вероятность интроверсии составляет 0.477 (47.7%), экстраверсии — 0.432, а амбиверсии — 0.091.
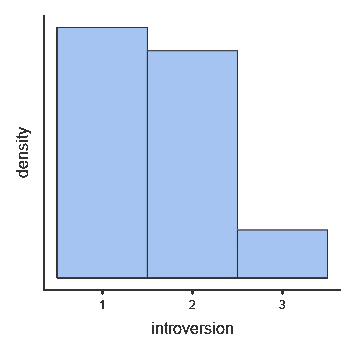
Полученная гистограмма (соответствующая таблице) изображена на рис. 2.3(3)j.
Рис. 2.3(3)j. Гистограмма распределения интроверсии/экстраверсии
Упражнение 2.3(4)j. В файле TempProb.sav содержатся данные о выраженности темперамента у жителей того же города. В переменной temp приведена принадлежность жителей к одному из четырех типов темперамента: 1 — холерик, 2 — сангвиник, 3 — флегматик, 4 — меланхолик или 5 — к неопределенному типу. Исходя из положения, что эти данные соответствуют генеральной совокупности, рассчитайте вероятности того, что случайный житель будет обладать тем или иным типом темперамента.
Пример 2.3(5)j. Смоделируем ситуацию выборочной оценки распределения вероятностей в генеральной совокупности. Допустим, в городе, о котором шла речь в Примере 2.3(1)j, проводится исследование, направленное на оценку соотношения интровертов и экстравертов. Исследование проводится неким институтом и этим проектом занимаются 10 исследователей. Каждый из исследователей тестирует 100 случайно отобранных жителей города. Таким образом, каждый из них получает выборку размером 100, а при объединении всех набранных данных можно получить большую выборку размером 1000. В файле IntroProbResearch.sav содержатся модельные данные такого исследования тысячи человек десятью исследователями. В первом столбце так же, как и в предыдущем примере, отмечена принадлежность испытуемых к интровертам, экстравертам или амбивертам, а во втором — ResearcherId — условный номер исследователя, который собрал эти данные (от 1 до 10). Сравним результаты, полученные отдельными исследователями, между собой и с данными из Примера 2.3(1)j Для этого можно использовать функцию разбиения файла: последовательно выбрать пункты меню, как в примере 2.3(1)j (убрав галочки в окне Statistics), но дополнительно перетащить переменную researcher_id в окно Split by. Гистограммы в этот раз делать не будем.
Мы получим таблицу 2.3(5)j
| introversion | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||||
| 1 | 53 | 44 | 55 | 49 | 57 | 49 | 41 | 49 | 50 | 47 | |||||||||||
| 2 | 43 | 49 | 42 | 43 | 36 | 40 | 47 | 40 | 40 | 43 | |||||||||||
| 3 | 4 | 7 | 3 | 8 | 7 | 11 | 12 | 11 | 10 | 10 | |||||||||||
При этом различия между данными, полученными различными исследователями, будут довольно заметны. Например, доли интровертов, экстравертов и амбивертов по данным исследователя номер 3 будут 0.55, 0.42 и 0.03, а если мы возьмем данные, полученные исследователем номер 10, то доли будут 0.5, 0.4 и 0.1 соответственно.
Упражнение 2.3(6)j. Соотнесите результаты, полученные каждым из 10 исследователей с данными «генеральной совокупности». Насколько они отличаются от данных, полученных в генеральной совокупности?
Как будет соотноситься результат каждого из исследователя с «истинным» распределением типов личности в генеральной совокупности, если каждый исследователь обследует не 100, а только 10 жителей города? А если каждый сумеет обследовать 1000 жителей? В каком случае полученные данные будут более схожими с генеральной совокупностью?
Пример 2.3(7)j. Если мы объединим выборки, полученные 10 исследователями в одну большую «мета-выборку», то мы получим данные в общей сложности на 1000 случайных респондентов. Проведение частотного анализа соотношения типов личности в объединенной выборке даст результат, приведенный в таблице 2.3.4(8)j.
Таблица 2.3(8)j. Распределение типов личности в объединенной выборке (1000 человек)
| Levels | Counts | % of Total | Cumulative % | ||||
| 1 | 494 | 49.4 % | 49.4 % | ||||
| 2 | 423 | 42.3 % | 91.7 % | ||||
| 3 | 83 | 8.3 % | 100.0 % | ||||
Как видно из таблицы, полученные частоты того или иного типа личности уже достаточно близки к полученным в генеральной совокупности (ср. с таблицей 2.3(2)j).
Данный пример наглядно демонстрирует, что недостаточный объем выборки может приводить к искажению оценки вероятности того или иного события (или значения параметра) в генеральной совокупности. В дальнейшем мы обсудим закон больших чисел, которые строго показывает, что увеличение выборки приводит к все более точной оценке «истинного» значения любого параметра в генеральной совокупности.
Пример 2.3(13). Рассмотрим ситуацию биномиального эксперимента, описанного в подпараграфе 2.2.4, в котором подбрасывают три монеты и считают количество выпавших гербов. Теоретические вероятности выпадения 0, 1, 2 и 3 в случае симметричной монеты равны 1/8, 3/8, 3/8 и 1/8 соответственно (см. 2.2.4). В файле 3FairCoins.sav приведены смоделированные данные эксперимента, в котором три монеты подбрасывают 1000 раз и каждый раз фиксируют количество гербов (единственный столбец — heads). Результаты расчета частоты появления каждого из возможных исходов представлены в таблице 2.3(14)j.
Таблица 2.3(14)j. Частота выпадения k гербов при подбрасывании трех монет
| Levels | Counts | % of Total | Cumulative % | ||||
| 0 | 127 | 12.7 % | 12.7 % | ||||
| 1 | 377 | 37.7 % | 50.4 % | ||||
| 2 | 375 | 37.5 % | 87.9 % | ||||
| 3 | 121 | 12.1 % | 100.0 % | ||||
Из таблицы видно, что относительная частота достаточно близка к рассчитанным выше теоретическим вероятностям.
Упражнение 2.3.(15)j. В файле 3UnknownCoins.sav содержатся модельные результаты трех серий экспериментов, аналогичных описанному в предыдущем примере. Однако в одном из экспериментов использовались симметричные монеты, а в двух других искривленные так, что в одной серии более вероятным было выпадение герба, а в другой — выпадение цифры. Данные представлены в трех столбцах (heads1, heads2 и heads3). Порядок серий с симметричными и асимметричными монетами неизвестен. Мы предлагаем читателю самостоятельно рассчитать частоты выпадения того или иного числа гербов и определить, в какой переменной содержатся данные об эксперименте с симметричной монетой, а в каких — данные об искривленных в пользу орла или цифры монетах.
2.3.3 Вероятности и частоты в Rstudio
Таблица содержит очень большое количество измерений этих двух параметров (426 679), статистика соответствует данным, накопленным на сайте http://psyline.retter.ru/auzeng/st_e.php (по состоянию на май 2016 года).
Выведем теперь две таблицы частот в консоль:
Из последней таблицы следует, что вероятность интроверсии составляет с точностью до третьего знака после запятой [4] 0.477 (47.7%), экстраверсии — 0.432, а амбиверсии — 0.091.
мы получим график, изображенный на рис. 2.3(3)r.
Рис. 2.3(3)r. Гистограмма распределения интроверсии/экстраверсии
Упражнение 2.3(4)r. В файле TempProb.sav содержатся данные о выраженности темперамента у жителей того же города. В переменной temp приведена принадлежность жителей к одному из четырех типов темперамента: 1 — холерик, 2 — сангвиник, 3 — флегматик, 4 — меланхолик или 5 — к неопределенному типу. Исходя из положения, что эти данные соответствуют генеральной совокупности, рассчитайте вероятности того, что случайный житель будет обладать тем или иным типом темперамента.
В результате мы получим следующую таблицу:
Как видно, различия между данными, полученными отдельными исследователями, будут довольно заметны. Например, доли интровертов, экстравертов и амбивертов по данным исследователя номер 3 будут 0.55, 0.42 и 0.03, а если мы возьмем данные, полученные исследователем номер 10, то доли будут 0.5, 0.4 и 0.1 соответственно.
Упражнение 2.3(6)r. Соотнесите результаты, полученные каждым из 10 исследователей с данными «генеральной совокупности». Насколько они отличаются от данных, полученных в генеральной совокупности?
Как будет соотноситься результат каждого из исследователя с «истинным» распределением типов личности в генеральной совокупности, если каждый исследователь обследует не 100, а только 10 жителей города? А если каждый сумеет обследовать 1000 жителей? В каком случае полученные данные будут более схожими с генеральной совокупностью?
Пример 2.3(7)r. Если мы объединим выборки, полученные 10 исследователями в одну большую «мета-выборку», то мы получим данные в общей сложности на 1000 случайных респондентов. Проведение частотного анализа соотношения типов личности в объединенной выборке даст следующий результат:
Получить относительные частоты можно с помощью уже упомянутой нами функции prop.table:
Как видно из таблиц, полученные частоты того или иного типа личности уже достаточно близки к полученным в генеральной совокупности (ср. с таблицей в примере 2.3(1)r).
Данный пример наглядно демонстрирует, что недостаточный объем выборки может приводить к искажению оценки вероятности того или иного события (или значения параметра) в генеральной совокупности. В дальнейшем мы обсудим закон больших чисел, которые строго показывает, что увеличение выборки приводит к все более точной оценке «истинного» значения любого параметра в генеральной совокупности.
Пример 2.3(13)r [8] . Рассмотрим ситуацию биномиального эксперимента, описанного в подпараграфе 2.2.4, в котором подбрасывают три монеты и считают количество выпавших гербов. Теоретические вероятности выпадения 0, 1, 2 и 3 в случае симметричной монеты равны 1/8, 3/8, 3/8 и 1/8 соответственно (см. 2.2.4). В файле 3FairCoins.sav приведены смоделированные данные эксперимента, в котором три монеты подбрасывают 1000 раз и каждый раз фиксируют количество гербов (единственный столбец — heads). Результаты расчета частоты появления каждого из возможных исходов представлены ниже:
Из таблиц видно, что относительная частота достаточно близка к рассчитанным выше теоретическим вероятностям.
Упражнение 2.3.(15)r. В файле 3UnknownCoins.sav содержатся модельные результаты трех серий экспериментов, аналогичных описанному в предыдущем примере. Однако в одном из экспериментов использовались симметричные монеты, а в двух других искривленные так, что в одной серии более вероятным было выпадение герба, а в другой — выпадение цифры. Данные представлены в трех столбцах (heads1, heads2 и heads3). Порядок серий с симметричными и асимметричными монетами неизвестен. Мы предлагаем читателю самостоятельно рассчитать частоты выпадения того или иного числа гербов и определить, в какой переменной содержатся данные об эксперименте с симметричной монетой, а в каких — данные об искривленных в пользу орла или цифры монетах.
[1] Скрипт, содержащий команды данного примера можно скачать здесь.
[2] Для того, чтобы узнать структуру таблицу и типы переменных в ней можно использовать функцию str (от structure): Str(data_prob). Также можно посмотреть состав таблицы и типы переменных, найдя её во вкладке Enviroment в правом верхнем углу окна Rstudio и раскрыв её, щёлкнув по значку.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.