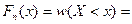Что такое вариационный ряд в математике

Вариационные ряды

Главная > Учебные материалы > Математика: Вариационные ряды

1.Вариационный ряд. 2.Числовые характеристики вариационного ряда.

1.Вариационный ряд.

Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.

Таб.1

По данным таблицы построим полигон распределения частот (рис.1)

В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.

Таб. 2

По данным таблицы построим гистограмму распределения частот (рис.2)

Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.

2.Числовые характеристики вариационного ряда.

Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости.

Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической.

Дисперсией s 2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической.

Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии.

Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака.

Пример.

В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины.

Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен.

Как видно из таблицы сумма произведений x i n i = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда.

По данным таблицы построим гистограмму распределения частот.

Построим и эмпирическую функцию распределения случайной величины (кумуляту).

Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:

Источник

Что такое вариационный ряд в математике

В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.

Это обстоятельство приводит к мысли построить статистические характеристики:

Пример 156. Имеются данные о количестве студентов в 30 группах физико-математического факультета:

26	25	25	26	25	23
23	24	19	23	20	19
22	24	24	23	20	23
24	19	21	18	21	18
20	18	18	21	15	15

Найти вариационный ряд количества студентов в группах и размах варьирования. Построить полигон частот.

Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:

15	18	19	20	21	22	23	24	25	26
2	4	2	4	3	1	5	4	3	2

Для построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты и полученные точки соединим отрезками.

Пример 157. Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающие числа. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:

Кол-во баллов	13	14	15	16	17	18	19	20
Кол-во школьников	2	3	2	4	12	10	8	9

Составить статистическое распределение количества школьников по количеству набранных баллов и построить полигон относительных частот.

Решение. Пусть = <количество набранных баллов>, a = <относительные частоты>. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:

X	13	14	15	16	17	18	19	20
0,04	0,06	0,04	0,08	0,24	0,2	0,16	0,18

Пример 158. В 2002 году количество служб, представляющих гражданам жилищные субсидии, по сельским районам области распределено следующим образом:

Построить эмпирическую функцию распределения.

Решение. Найдем сначала статистический ряд распределения числа служб в районах области.

Эмпирическую функцию распределения находим аналогично интегральной функции (см. §13 ) [перейти].

Пример 159. Построить гистограмму следующей выборки объема 50

Решение. Найдем плотность относительной частоты для каждого интервала и заполним последний столбец таблицы:

Из способа построения гистограммы следует, что полная ее площадь равна единице.

Построить гистограмму распределения числа школ по районам области.

Решение. Выберем границы интервалов и составим по данной выборке следующую таблицу

Аналогично предыдущему примеру строим гистограмму числа школ, распределенных по малым городам и районам области.

«Сглаживая» полученную гистограмму, получаем «похожесть» данного дискретного закона распределения на классический показательный (непрерывный) закон. В этом и заключается основное предназначение гистограмм выборок.

Вопросы для самоконтроля

На каких методах основано изучение статистических данных?

Основные задачи математической статистики.

Какие способы отбора из генеральной совокупности вы знаете?

Какая выборка называется представительной?

В чем отличие вариационного от статистического ряда?

Для чего используется полигон частот?

Свойства эмпирической функции распределения.

В каком случае и для чего строятся гистограммы?

I. 311. Записать выборку 2, 7, 3, 5, 4, 10, 5, 5, 2, 8, 10, 2, 7, 7, 7, 5, 4, 2, 4, 7, 8 в виде: а) вариационного ряда; б) статистического ряда.

312. Найдите эмпирическую функцию распределения для выборки, представленной вариационным рядом:

1	2	4	7
10	20	30	40

313. Имеются данные о количестве сельских населенных пунктов районов Ярославской области с численностью населения более 500 человек:

Найдите вариационный ряд количества населенных пунктов Ярославской области с численностью населения более 500 человек. Постройте полигон частот.

314. В 2002 году количество крупных и средних промышленных предприятий по районам ( в том же порядке, что и в предыдущей задаче) области распределено следующим образом:

Постройте полигон частот и эмпирическую функцию распределения.

315. Количество учащихся, получивших аттестат с медалью, в 2001 году по городам и районам Ярославской области:

Найдите вариационный ряд распределения медалистов, размах варьирования и среднее число медалистов по городам и районам области.

316. Посевные площади картофеля (тыс. гектаров) в сельских хозяйствах Ярославской области по районам:

1,5; 1,5; 0,6; 1,3; 0,9; 0,9; 0,6; 1,3; 1,1; 0,6; 1,1; 0,9; 1,6; 1,3; 0,8; 0,4; 1,1.

Найдите статистический ряд распределения посевных площадей и постройте полигон относительных частот.

—Сумма частот вариант интервала

Источник

ЛЕКЦИЯ 19. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. ПРЕДМЕТ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ. ВАРИАЦИОННЫЕ РЯДЫ

Математическая статистика – это раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических целей.

Статистическими данными называются сведения о числе и характере объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными свойствами.

Метод исследования, опирающийся на рассмотрение статистических данных от тех или иных совокупностей объектов, называется статистическим.

Формальная математическая сторона статистических методов исследования безразлична к природе исследуемых объектов и составляет предмет математической статистики.

Основная задача математической статистики состоит в получении выводов о массовых явлениях и процессах по данным наблюдений над ними или экспериментов.

Статистика – наука, которая позволяет увидеть закономерности в хаосе случайных данных, выделить установившиеся связи в них и определить наши действия, чтобы увеличить долю правильно принятых решений.

Многие известные сейчас зависимости между различными аспектами окружающего нас мира получены путем анализа накопленных человечеством данных. После статистического обнаружения зависимостей человек уже находит то или иное рациональное объяснение обнаруженным закономерностям.

Для изложения начальных определений статистики обратимся к примеру.

Пример. Предположим, необходимо оценить степень изменения коэффициента интеллектуальности за 3 года обучения у 100 студентов. В качестве показателя рассмотрим отношение нынешнего коэффициента к ранее измеренному коэффициенту (три года назад), умноженному на 100 %.

Получим последовательность 100 случайных величин: 97,8; 97,0; 101,7; 132,5; 142; …; 122. Обозначим ее через Х.

Определение 1. Последовательность наблюдаемых в результате исследования случайных величин Х в статистике называется признаком.

Определение 2.Различные значения признака называются вариантами.

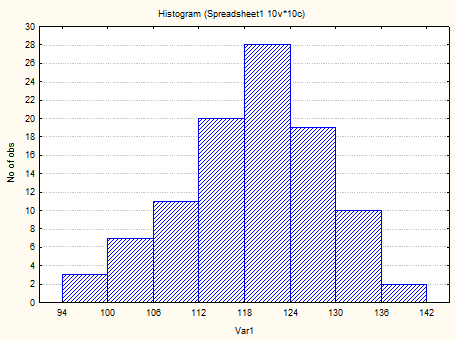
Из приведенных значений вариант трудно получить некоторую информацию о динамике изменения коэффициента интеллектуальности в процессе обучения. Упорядочим данную последовательность по возрастанию: 94; 97,0; 97,8; …142. Из полученной последовательности уже можно извлечь некоторую полезную информацию – например, легко определить минимальное и максимальное значения признака. Но не видно, как распределен признак среди всей совокупности обследуемых студентов. Разобьем варианты на интервалы. Согласно формуле Стерджеса, рекомендуемое число интервалов

m = 1+3,32lg(n) ≈ 7,6, а величина интервала .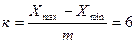

Диапазоны полученных интервалов приведены в столбце 1 таблицы.

Посчитаем, сколько значений признака попало в каждый интервал, и запишем в столбец 3.

Определение 3.Число, показывающее, сколько вариант попало в данный i-й интервал, называется частотой и обозначается n_i.

Определение 4.Отношение частоты к общему числу наблюдений называется относительной частотой (w_i) или весом.

Определение 5.Вариационным рядом называется расположенный в порядке возрастания или убывания ряд вариантов с соответствующими им весами.

Для данного примера вариантами являются середины интервалов.

Определение 6.Накопленной частотой (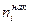) называется число вариант со значением признака меньшим, чем х (хÎR).

i	Интервал	ni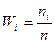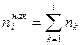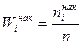
94-100	0,03	0,03
100-106	0,07	0,1
106-112	0,11	0,21
112-118	0,2	0,41
118-124	0,28	0,69
124-130	0,19	0,88
130-136	0,1	0,98
136-142	0,02

Определение 7. Отношение накопленной частоты к общему числу наблюдений называется относительной накопленной частотой ().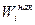

Из таблицы уже можно сделать ряд полезных выводов:

– у большинства студентов значение коэффициента интеллектуальности увеличилось (97 чел.);

– у большинства студентов (48 чел.) увеличение составило от 112 % до 124 %;

– у двенадцати студентов увеличение произошло более чем на 130 %;

– закон распределения признака «напоминает» нормальное распределение.

Определение 8. Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и называется непрерывным (интервальным), если варианты могут отличаться друг от друга на сколь угодно малую величину.

Примером дискретного ряда является распределение студентов по полученным отметкам по дисциплине «Теория вероятностей и математическая статистика»:

Отметка

ni

ni накоп.

Для визуализации вариационных рядов наиболее часто используют полигон, гистограмму, кумулятивную кривую.

Определение 9. Гистограммой называется ступенчатая фигура из прямоугольников с основаниями, равными интервалам значения признака и высотами, равными частотам или накопленным частотам.

Гистограмма используется только для изображения интервальных вариационных рядов. На рис.1 приведена гистограмма для вариационного ряда, рассмотренного ранее примера.

Определение 10.Полигоном называется ломанная линия, в которой концы отрезков имеют координаты (x_i,n_i) или (x_i,w_i).

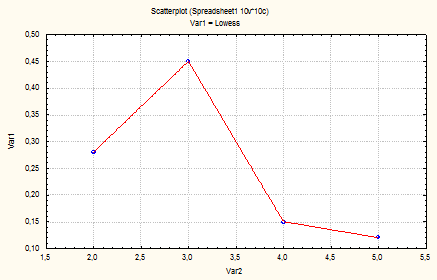
Полигон служит, как правило, для изображения дискретных вариационных рядов. На рис.2 изображен полигон для вариационного ряда распределения оценок среди ста студентов по курсу «Теория вероятностей и математическая статистика».

Определение 11. Кумулятивная кривая – это кривая накопленных частот.

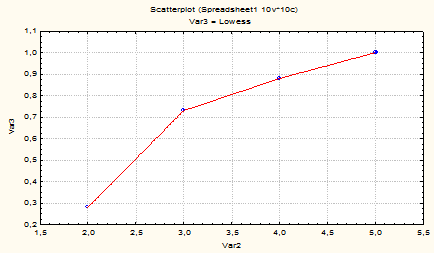
На рис.3 приведена кумулятивная кривая оценок студентов по «Теории вероятностей и математической статистике».

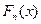
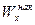
Определение 10.Эмпирической функцией распределения называется относительная частота события, что признак Х примет значение меньшее, чем заданное х (хÎR), т.е.

.

Эмпирическая функция распределенияоценок по «Теории вероятностей и математической статистике» имеет вид

.

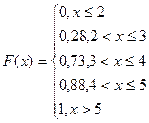
График ее изображен на рис.4.

1

0,88

0,73

0,28

Вариационный ряд и графические формы его визуализации содержат достаточно полную информацию об изменчивости признака. Но обилие числовых данных, с помощью которых он задается, усложняет процедуру их применения.

На практике часто оказывается достаточным рассмотрение числовых характеристик вариационных рядов (средних, характеристик изменчивости и т.д.). Такие числовые характеристики называются статистическими характеристиками признака.

Источник