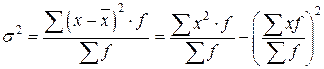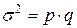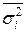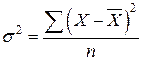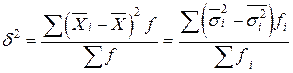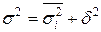Что такое вариация в статистике

Вариация понятие, относительные и абсолютные показатели, способы их расчета

Этот термин ведёт своё происхождение от латинского слова «varito». Оно переводится как «изменение» или «различие».

Вариация это количественная мера изменения определённых данных, которая помогает исследовать её случайные изменения. Для их анализа применяют различные статистические методы.

О них будет более подробно рассказано в этой статье.

Онлайн-калькулятор показателей вариации

Показатели вариации в статистике

Статистика широко применяется в самых различных областях. Она доказала свою пользу не только в естественных науках, но и в изучении различных социологических явлений, изменений цен, а также в других ситуациях.

Эта наука имеет дело со случайными величинами, изменение которых требует для своего описания использования специальных характеристик. Наиболее известной из них является средняя. Однако, хотя она и включает в себя некоторый объём информации, тем не менее не даёт возможности найти информацию о разбросе случайных данных, а также дать понятие о динамике изменения и наиболее вероятных тенденциях в дальнейшем.

Математический аппарат для изучения вариационных процессов использует характеристики, способы расчёта которых можно разделить на три группы.

Показатели размаха изменений говорят о том, какова разница между максимальными отклонениями исследуемых чисел:

Данные, относящиеся ко второй категории, можно считать так:

Для расчёта относительных показателей применяется:

Далее будет рассказано о наиболее часто применяемых математических характеристиках рассматриваемого понятия.

При проведении статистических вычислениях удобно пользоваться электронными таблицами Excel.

Абсолютные показатели вариации

Когда говорят об абсолютных показателях вариации, имеют в виду следующие методы для проведения статистического анализа:

Размах вариации

При рассмотрении изменения исследуемых данных, одной из важных характеристик является размах вариации.

Он равен разности между максимальной и минимальной границами. Посмотрим, как это характеристика исчисляется.

Формула выглядит так:

РВар = ЗнМакс — ЗнМин,

Пример.

Эта формула может быть применена, например, в следующей ситуации. Предположим, рассматривается рост отобранных случайным образом людей. В этой совокупности десять человек и рост их равен: 165, 172, 179, 190, 182, 171, 191, 183, 177 и 178 сантиметров. Эти цифры составляют совокупность значений случайных данных.

Как можно увидеть в рассматриваемом случае, минимальный рост в этой группе людей составляет 165 см, а максимальный — 191 см. Разница между ними составляет 191 — 165 = 26 см. Таким образом, рассматриваемое значение для определённой таким образом совокупности данных показывает 26 см.

Отклонение вариации

Здесь рассматривается отклонение изучаемой случайной величины. Для того, чтобы его вычислить, необходимо сначала определить её среднее значение.

Чтобы посчитать, необходимо просуммировать все значения случайных данных и затем разделить на их количество. Получившаяся величина представляет собой нужный результат.

В некоторых формулах используются значения весов, придаваемых каждому значению. Кратко говоря, они назначаются в соответствии с целями проведения статистического исследования. Веса обычно подбираются таким образом, чтобы их сумма была равна единице.

Среднее линейное простое

Оценка величины отклонения рассчитывается так:

Формула выглядит таким образом:

СЛП = (|x(1) – x0| + |x(2) – x0| + … + |x(n) – x(0)|) / n,

Вертикальные чёрточки используются для того, чтобы показать, что здесь вычисляется абсолютная разность.

Среднее линейное взвешенное

Для этого потребуется формула:

СЛВ = (|x(1) – x0|*f(1) + |x(2) – x0|*f(2) + … + |x(n) – x(0)|*f(n)) / n,

Остальные обозначения рассмотрены ранее.

Среднее квадратическое отклонение

В этом случае результат определяется по другому правилу, чем в прежних случаях:

СКО = SQRT(((x(1) – x0)**2 + (x(2) – x0)**2 + … + (x(n) – x(0))**2) / n),

Дисперсия (простая, взвешенная)

Простая дисперсия равна СКО, возведённому в квадрат.

Взвешенная называется так потому, что каждое слагаемое умножается на свой вес.

Здесь применяется формула:

ДВ = (f(1)*(x(1) – x0)**2 + f(2)*(x(2) – x0)**2 + … + f(n)*(x(n) – x(0))**2) / n*(f(1) + f(2) + … + f(n)),

где: ДВ представляет собой дисперсию взвешенную.

Вариация альтернативного признака

Это понятие характеризует те ситуации, когда часть предметов выборки обладает определённым свойством, а другая — нет:

СРЕД = ((1-p) + (0-p)) / (p+q) = p,

ВАР = (q*(1-p)**2+ q*(0-p)**2) / (p+q) = pq.

Здесь СРЕД обозначает среднее, а p и q представляют собой положительные числа, в сумме дающие единицу.

ВАР обозначает искомую величину.

Относительные показатели вариации

В данном случае рассматриваются отношение отклонения и среднего конкретной выборки. Для различных характеристик используются различные способы определения среднего отклонения.

Чем меньше полученный коэффициент, тем более сгруппированы данные. Этот коэффициент не имеет единиц измерения.

Коэффициент осцилляции

Эта величина равна частному от деления размаха вариации на среднее случайной величины.

Коэффициент вариации

Такой коэффициент можно рассчитать путём деления линейного отклонения на такой же знаменатель, как в предыдущем случае.

Относительное линейное отклонение

В данном случае искомое значение рассчитывается как результат деления среднего квадратического на этот же знаменатель.

Примеры расчетов

Здесь будет приведены примеры расчётов. Рассматривается ситуация, когда пять человек устраиваются на новую работу. В данной специальности они проработали различное количество лет: 2, 3, 4, 7 и 9 лет.

X(0) = (2 + 3 + 4 + 7 + 9) / 5 = 25 / 5 = 5.

СЛП = (|x(1) – x0| + |x(2) – x0| + … + |x(n) – x(0)|)/n = (|2 5| + |3 5| + |4 5| + |7 5| + |9 – 5|) / 5 = (3 + 2 + 1 + 2 + 4) / 5 = 12 / 5 = 2,4 года.

СКО = SQRT(((x(1) – x0)**2 + (x(2) – x0)**2 + … + (x(n) – x(0))**2)/n) = SQRT(((2 – 5)**2 + (3 – 5)**2 + (4 – 5)**2 + (7 – 5)**2 + (9 – 5)**2) / 5) = SQRT((3**2 + 2**2 + 1**2 + 2**2 + 4**2)/5) = SQRT ((9 + 4 + 1 + 4 + 16) / 5) = SQRT(34 / 5) = SQRT(6,80) = 2,61 года (приблизительное значение).

Последнее значение равно СКО, возведённому в квадрат.

В большинстве случаев расчет представляет собой гораздо более сложную задачу, чем показано в приведённом примере. Для облегчения процесса вычислений можно использовать онлайн калькулятор.

Заключение

Изучение случайных процессов играет важную роль в науке, экономике и общественной жизни. Для того, чтобы получить максимальное количество информации при их изучении, нужно активно использовать статистические методы, в том числе те, которые связаны с вариацией.

Источник

Статистическое изучение вариации

Тема 5

Основные вопросы: 1. Понятие вариации.

2. Показатели вариации.

3. Относительные показатели вариации.

1. Понятие вариации. При изучении совокупности явления нельзя ограничиваться только нахождением средней величины. Средние величины дают обобщенную характеристику варьирующего признака, показывают типичные характеристики для изучаемой совокупности. Однако в средней величине не проявляется степень колеблемости отдельных значений признаков вокруг среднего уровня. В зависимости от однородности в совокупности колеблемость признаков может быть большой или малой. Поэтому возникает необходимость в измерении вариации отдельных вариантов по отношению к средней величине.

Определение: Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Вариация в переводе с латинского означает «колеблемость», «изменчивость», «непостоянство». Предполагая, что большинство социально-экономических явлений и процессов варьируют в некотором масштабе, статистика разработала методологию расчета показателей вариации, которые, в свою очередь, могут быть абсолютными, относительными и средними.

Величины признаков колеблются, варьируют под действием различных причин и условий, которые в статистике называют факторами. Нередко эти факторы действуют в противоположных направлениях и сами, в свою очередь, варьируют. Среди них есть существенные факторы, определяющие величину вариантов данного признака у всех единиц совокупности. Но есть и несущественные, которые на одни единицы совокупности могут оказывать влияние, на другие нет.

Например, вариация оценок студентов на экзамене в вузе вызывается, в частности, различными способностями студентов; временем, затраченным ими на самостоятельную работу; посещаемостью занятий; различием социально-бытовых условий и т.д. Но на оценку могут влиять и какие-либо привходящие, чисто случайные причины, например, временное недомогание.

Вариация, порождаемая существенными факторами, носит систематический характер, то есть наблюдается последовательное изменение вариантов признака в определенном направлении. Такая вариация называется систематической. В систематической вариации проявляются взаимосвязи между явлениями, их признаками, в такой связи – один как причина, другой как следствие его действия.

Вариация, обусловленная случайными факторами, называется случайной вариацией. Здесь не наблюдается систематического изменения вариантов зависимого признака от случайных факторов; все изменения носят хаотический характер, поскольку нет устойчивой связи этих факторов с единицами изучаемой совокупности.

Вариация зависимого признака, образовавшаяся под действием всех без исключения влияющих на него факторов, называется общей вариацией. Следовательно, общая вариация слагается из систематической и случайной вариации.

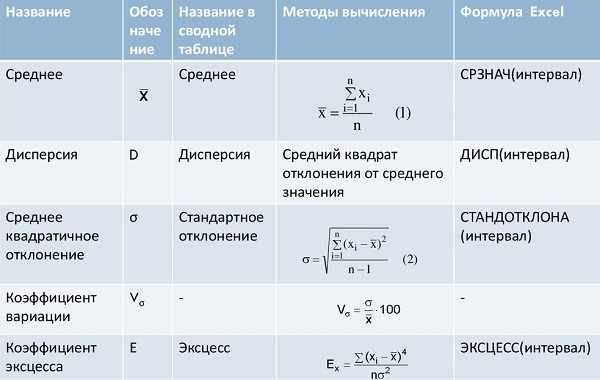
2. Показатели вариации. К показателям вариации относятся: размах вариации, среднее линейное (абсолютное) отклонение (с.л.о.), дисперсия, среднее квадратическое отклонение (с.к.о.), коэффициент вариации.

1) Размах вариации – разность между максимальным и минимальным значением признака:

.

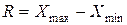
Он характеризует пределы изменения признака.

Средний размах: 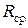– это есть средняя арифметическая из ряда размахов, полученных из серии равных по объему наблюдений. Используется в контроле качества.

Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.

Простейший показатель такого типа СЛО.

2). Среднее линейное отклонение (СЛО) – представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (учитывает только крайние значения признака и не учитывает все промежуточные).

– СЛО для несгруппированных данных: ,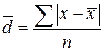

где 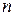– число членов ряда.

Т.е. 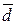– СЛО равно средней арифметической из абсолютных отклонений (модулей) признака всех единиц совокупности от средней арифметической.

– СЛО для сгруппированных данных: ,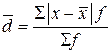

где 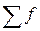– сумма частот вариационного ряда.

В формулах разности в числителе взяты по модулю, иначе в числителе всегда будет ноль – алгебраическая сумма отклонений вариантов от их средней арифметической.

Поэтому СЛО применяют редко, только в случаях, когда суммирование показателей без учета знаков имеет экономический смысл. Например, анализ состава рабочих, ритмичность производства, оборот внешней торговли.

3) Дисперсия – это средний квадрат отклонений индивидуальных значений от средней арифметической (не имеет единиц измерения).

В общем виде взвешенная дисперсия исчисляется по формуле:

или простая дисперсия:

.

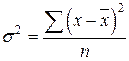
Дисперсия альтернативного признака:

4) Среднее квадратическое отклонение (СКО) ‑ это есть квадратный корень из среднего квадрата отклонений отдельных значений признака от средней арифметической:

– для несгруппированных данных;

– для сгруппированных данных (для вариационного ряда).

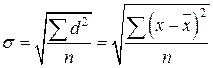
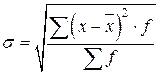
3. Относительные показатели вариации (коэффициент вариации). В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией зарплаты, выраженной в рублях.

Для осуществления такого сравнения, а также сравнения колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации – коэффициент вариации (КВ).

КВ – представляет собой выраженное в процентах отношение СКО к средней арифметической.

,

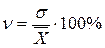
это и есть коэффициент вариации. Это относительная мера вариации и позволяет сравнивать степень варьирования в разных вариационных рядах.

Определение: Дисперсия – это средний квадрат отклонений всех значений признака ряда распределения от средней арифметической.

1) Дисперсия постоянной величины равна нулю ();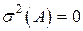

2) Дисперсия не меняется, если все варианты увеличить или уменьшить на одно и то же число ();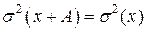

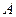
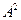
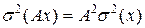
3) Если все варианты умножить на число , дисперсия увеличится в раз ;

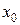
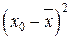
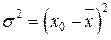
4) Дисперсия от средней меньше, чем средний квадрат отклонений от любого числа на – свойство минимальности дисперсии от средней ().

Использование свойств дисперсии позволяет упрощать ее расчеты, особенно в случаях, когда вариационный ряд составляет арифметическую прогрессию или имеет равные интервалы. В этих случаях сначала находят дисперсию от условного нуля, а затем используют 4-е свойство, переходят к дисперсии от средней.

Виды дисперсий для сгруппированных данных, условия их применения в статистических исследованиях.

Если совокупность данных сгруппирована на группы по какому-то признаку, то в этом случае выделяются 3 вида дисперсий:

— Общая дисперсия

– Средняя из внутригрупповых дисперсий

— Межгрупповая дисперсия

Общая 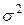— измеряет вариацию во всей совокупности

Средняя из внутригрупповых дисперсий исчисляется ,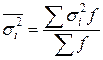

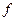
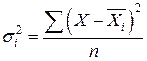
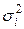
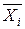
где – частота появления внутригрупповой дисперсии одной величины (одного размера).

– внутригрупповая — измеряет вариацию признака внутри группы, — групповая средняя.

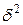
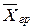
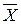
Межгрупповая дисперсия – измеряет колеблемость групповых средних вокруг общей средней :

Она измеряет вариацию, обусловленную признаком, положенным в основу группировки.

Правило сложения дисперсий.

Общий закон (правило) сложения дисперсий ‑ Общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии.

Показывает значение фактора, положенного в основу группировки (из всей совокупности факторов).

Коэффициент детерминации – есть квадрат эмпирического корреляционного отношения.

Эмпирическое корреляционное отношение – есть корень квадратный из отношения межгрупповой дисперсии к общей:

– характеризует влияние группировочного признака на результативный признак (оба показателя (числитель и знаменатель) не превышают по своей величине единицы: чем больше показатели в этих пределах, тем теснее взаимосвязь между изучаемыми признаками).

; – влияние других факторов равно 0.

– влияние признака равно 0.

Источник

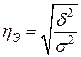
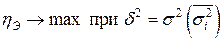
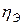
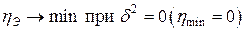
Показатели вариации

Поможем написать любую работу на аналогичную тему

Показатели вариации. При изучении варьирующего признака у единиц совокупности нельзя ограничиваться лишь расчетом средней величины из отдельных вариантов, так как одна и та же средняя может относиться далеко не к одинаковым по составу совокупностям.

Вариацией признака называется различие индивидуальных значений признака внутри изучаемой совокупности.

Термин «вариация» произошел от латинского variatio – изменение, колеблемость, различие. Однако не всякие различия принято называть вариацией.

Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Колеблемость отдельных значений характеризуют показатели вариации. Чем больше вариация, тем дальше в среднем отдельные значения лежат друг от друга.

Различают вариацию признака в абсолютных и относительных величинах.

К абсолютным показателям относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия. Все абсолютные показатели имеют ту же размерность, что и изучаемые величины.

К относительным показателям относятся коэффициенты осцилляции, линейного отклонения и вариации.

Показатели абсолютные. Рассчитаем абсолютные показатели, характеризующие вариацию признака.

Размах вариации, представляет собой разность между максимальным и минимальным значением признака.

Показатель размаха вариации не всегда применим, так как он учитывает только крайние значения признака, которые могут сильно отличаться от всех других единиц.

Более точно можно определить вариацию в ряду при помощи показателей, учитывающих отклонения всех вариантов от средней арифметической.

Таких показателей в статистике два: среднее линейное и среднее квадратическое отклонение.

Среднее линейное отклонение (L) представляет собой среднее арифметическое из абсолютных значений отклонений отдельных вариантов от средней.

– для несгруппированных данных;

– для сгруппированных данных.

Практическое использование среднего линейного отклонения заключается в следующем, с помощью этого показателя анализируется состав работающих, ритмичность производства, равномерность поставок материалов.

Недостаток этого показателя заключается в том, что он усложняет расчеты вероятного типа, затрудняет применение методов математической статистики.

Среднее квадратическое отклонение () является наиболее распространенным и общепринятым показателем вариации. Оно несколько больше среднего линейного отклонения. Для умеренно асимметричных распределений установлено следующее соотношение между ними

=1,25L

Для его исчисления каждое отклонение от средней возводится в квадрат, все квадраты суммируются (с учетом весом), после чего сумма квадратов делится на число членов ряда и из частного извлекается корень квадратный.

Все эти действия выражает следующая формула

– для несгруппированных данных,

– для сгруппированных данных.

т.е. среднее квадратическое отклонение представляет собой корень квадратный из средней арифметической квадратов отклонений от средней.

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше σ, тем лучше среднее арифметическое отражает собой всю представляемую совокупность.

Средняя арифметическая из квадратов отклонений вариантов значений признака от средней величины носит название дисперсии (), которая рассчитывается по формулам

– для несгруппированных,

– для сгруппированных.

Отличительной особенностью данного показатели является то, что при возведении в квадрат () удельный вес малых отклонений уменьшается, а больших увеличивается в общей сумме отклонений.

Дисперсия обладает рядом свойств, некоторые из них позволяют упростить её вычисление:

1. Дисперсия постоянной величины равна 0.

Если , то и .

Тогда .

2. Если все варианты значений признака (x) уменьшить на одно и то же число, то дисперсия не уменьшится.

Пусть , но тогда в соответствии со свойствами средней арифметической и .

Дисперсия в новом ряду будет равна

, т.е. дисперсия в ряду равна дисперсии первоначального ряда .

3. Если все варианты значений признака уменьшить в одно и то же число раз (k раз), то дисперсия уменьшится в k2 раз.

Пусть , тогда и .

Дисперсия же нового ряда будет равна

Выше был рассмотрен расчет показателей вариации для количественных признаков, но в экономических расчетах может ставиться задача оценки вариации качественных признаков. Например, при изучении качества изготовленной продукции, продукцию можно разделить на качественную и бракованную.

В таком случае речь идет об альтернативных признаках.

Альтернативными признаками называются такие, которыми одни единицы совокупности обладают, а другие нет. Например, наличие производственного стажа у абитуриентов, ученая степень у преподавателей ВУЗов и т.д. Наличие признака у единиц совокупности условно обозначаем через 1, а отсутствие – 0. Тогда, если долю единиц, обладающих признаком (в общей численности единиц совокупности), обозначить через р, а долю единиц, не обладающих признаком, через q, дисперсию альтернативного признака можно рассчитать по общему правилу. При этом p + q = 1 и, значит, q = 1– p.

Сначала рассчитываем среднее значение альтернативного признака:

Рассчитаем среднее значение альтернативного признака

,

т.е. среднее значение альтернативного признака равно доле единиц, обладающих данным признаком.

Дисперсия же альтернативного признака будет равна:

Таким образом, дисперсия альтернативного признака равняется произведению доли единиц, обладающих данным признаком, на долю единиц, не обладающих данным признаком.

А среднее квадратическое отклонение будет равно =.

Показатели относительные. Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях представляют интерес показатели вариации, выраженные в относительных величинах. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане.

Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Различают следующие относительные показатели вариации:

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.

.

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отношений от средней величины.

.

3. Коэффициент вариации оценивает типичность средних величин.

.

Чем меньше , тем однороднее совокупность по изучаемому признаку и типичнее средняя. Если ≤33%, то распределение близко к нормальному, а совокупность считается однородной. Из приведенного примера вторая совокупность однородна.

Виды дисперсий и правило сложения дисперсий. Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

При этом можно определить три показателя колеблемости признака в совокупности:

1. Общую вариацию совокупности, которая является результатом действия всех причин. Эта вариация может быть измерена общей дисперсией (), характеризующей отклонения индивидуальных значений признака совокупности от общей средней

.

2. Вариацию групповых средних, выражающих отклонения групповых средних от общей средней и отражающих влияние того фактора, по которому произведена группировка. Эта вариация может быть измерена так называемой межгрупповой дисперсией (δ2)

,

где — групповые средние, а -общая средняя для всей совокупности, и — численность отдельных групп.

3. Остаточную (или внутригрупповую) вариацию, которая выражается в отклонении отдельных значений признака в каждой группе от их групповой средней и, следовательно, отражает влияние всех прочих факторов кроме положенного в основу группировки. Поскольку вариацию в каждой группе отражает групповая дисперсия

,

то для всей совокупности остаточную вариацию будет отражать средняя из групповых дисперсий. Эту дисперсию называют средней из внутригрупповых дисперсий () и рассчитывается она по формуле

.

Общая вариация признака в совокупности должна определяться как сумма вариации групповых средних (за счет одного выделенного фактора) и остаточной вариации (за счет остальных факторов). Это равенство находит свое выражение в сложении дисперсий

.

Это равенство, имеющее строго математическое доказательство, известно, как правило сложения дисперсий.

Правило сложения дисперсий позволяет находить общую дисперсию по её компонентам, когда индивидуальные значения признака неизвестны, а в распоряжении имеются только групповые показатели.

Коэффициент детерминации. Правило сложения дисперсии позволяет выявить зависимость результатов от определенных факторов при помощи коэффициента детерминации.

,

Этот коэффициент показывает долю (удельный вес) общей вариации изучаемого признака, обусловленную вариацией группировочного признака.

Корень квадратный из коэффициента детерминации носит название корреляционного отношения ():

Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Корреляционное отношение изменяется в пределах от 0 до 1. Если , то группировочный признак не оказывает влияния на результативный. Если , то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю.

Показатели асимметрии и эксцесса. В области экономических явлений строго симметричные ряды встречаются крайне редко, чаще приходится иметь дело с асимметричными рядами.

В статистике для характеристики асимметрии пользуются несколькими показателями. Если учесть, что в симметричном ряду средняя арифметическая совпадает по значению с модой и медианой, то наиболее простым показателем асимметрии () будет разность между средней арифметической и модой, т.е. =.

Если ()>0, то на графике такой ряд будет иметь вытянутость вправо (правосторонняя асимметрия).

Если () 0, то эксцесс считают положительным (распределение островершинно), если

Источник