Что такое ведущий элемент в матрице

Алгоритм приведения матрицы к ступенчатому виду

Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия.

1. В первом столбце выбрать элемент, отличный от нуля (ведущий элемент). Строку с ведущим элементом (ведущая строка), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые.

2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить.

3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа).

4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы.

7. Теорема про розклад визначника по елементам рядка.

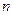
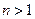
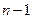
Теорема о разложении определителя по элементам строки или столбца позволяет свести вычисление определителя —го порядка () к вычислению определителей порядка .

Если определитель имеет равные нулю элементы, то удобнее всего разлагать определитель по элементам той строки или столбца, который содержит наибольшее число нулей.

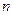
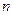
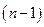
Используя свойства определителей, можно преобразовать определитель —го порядка так, чтобы все элементы некоторой строки или столбца, кроме одного, стали равными нулю. Таким образом, вычисление определителя —го порядка, если он отличен от нуля, сведется к вычислению одного определителя —го порядка.

Задача 3.1.Вычислить определитель

.

.

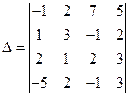
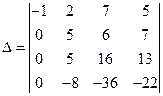
Разлагая определитель по элементам первого столбца, имеем

.

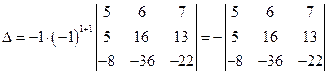
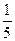
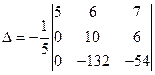
В полученном определителе 3-го порядка обратим в нуль все элементы первого столбца, кроме первого. Для этого ко второй строке прибавим первую, умноженную на (-1), к третьей, умноженной на 5, прибавим первую, умноженную на 8. Так как умножали третью строку на 5, то (для того, чтобы определитель не изменился) умножим его на . Имеем

.

Полученный определитель разложим по элементам первого столбца:

8. Теорема Лапласа(1). Теорема про чужі доповнення(2)

1)Определительравенсуммепроизведений элементов какой-либо строки на ихалгебраическиедополнения.

2)Суммапроизведенийэлементовкакой-либо строки определителя на алгебраические дополнения соответствующих элементов другой его строки равна нулю (теорема об умножении на чужие алгебраические дополнения).

9. Арифметичні векторні простори .

Всякая точка на плоскости при выбранной системе координат задается парой (α, β) своих координат; числа α и β можно понимать также как координаты радиуса-вектора с концом в этой точке. Аналогично, в пространстве тройка (α, β, γ) определяет точку или вектор с координатами α, β, γ. Именно на этом основывается хорошо известная читателю геометрическая интерпретация систем линейных уравнений с двумя или тремя неизвестными. Так, в случае системы двух линейных уравнений с двумя неизвестными

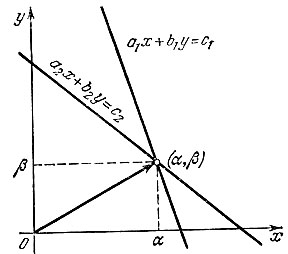
Рис. 26

Аналогично можно поступить с системой линейных уравнений с тремя неизвестными, интерпретируя каждое уравнение как уравнение плоскости в пространстве.

Хотя непосредственное геометрическое истолкование системы (1) при n > 3 уже невозможно, однако вполне возможно и во многих отношениях удобно распространить на случай произвольного n геометрический язык пространства двух или трех измерений. Этой цели и служат дальнейшие определения.

По аналогии с обычной плоскостью множество всех n-мерных векторов, удовлетворяющих линейному уравнению с n неизвестными, называют гиперплоскостью в n-мерном пространстве. При таком определении множество всех решений системы (1) есть не что иное, как пересечение нескольких гиперплоскостей.

Сложение и умножение n-мерных векторов определяются по тем же правилам, что и для обычных векторов. А именно, если

— два n-мерных вектора, то их суммой называется вектор

Произведением вектора а на число λ называется вектор

Множество всех n-мерных арифметических векторов с операциями сложения векторов и умножения вектора на число называется арифметическим n-мерным векторным пространством L_n.

Используя введенные операции, можно рассматривать произвольные линейные комбинации нескольких векторов, т. е. выражения вида

В трехмерном пространстве векторов особую роль играет тройка векторов i, j, k (координатные орты), по которым разлагается любой вектор а:

В n-мерном случае такую же роль играет следующая система векторов:

Обозначая через 0 вектор, все координаты которого равны нулю (кратко, нулевой вектор), введем следующее важное определение:

линейно зависимы, поскольку

Линейная зависимость, как видно из определения, равносильна (при k ≥ 2) тому, что хотя бы один из векторов системы является линейной комбинацией остальных.

Если система состоит из двух векторов a₁, а₂, то линейная зависимость системы означает, что один из векторов пропорционален другому, скажем, а₁ = λа₂; в трехмерном случае это равносильно коллинеарности векторов а₁ и а₂. Точно так же линейная зависимость системы I из трех векторов в обычном пространстве означает компланарность этих векторов. Понятие линейной зависимости является, таким образом, естественным обобщением понятий коллинеарности и компланарности.

Этот факт легко устанавливается на основании определения базиса.

Продолжая аналогию с трехмерным пространством, можно и в n-мерном случае определить скалярное произведение а · b векторов, полагая

При таком определении сохраняются все основные свойства скалярного произведения трехмерных векторов. Векторы а и b называются ортогональными, если их скалярное произведение равно нулю:

1) для любых векторов а, b, принадлежащих V, их сумма а + b также принадлежит V;

2) для любого вектора а, принадлежащего V, и для любого действительного числа λ вектор λа также принадлежит V.

Например, множество всех линейных комбинаций векторов e₁, е₂ из системы (5) будет подпространством пространства L_n.

Указанная система векторов называется базисом подпространства V.

Из определения пространства и подпространства непосредственно следует, что пространство L_n есть коммутативная группа относительно операции сложения векторов, а любое его подпространство V является подгруппой этой группы. В этом смысле можно, например, рассматривать смежные классы пространства L_n по подпространству V.

В заключение подчеркнем, что если в теории n-мерного арифметического пространства вместо действительных чисел (т. е. элементов поля действительных чисел) рассматривать элементы произвольного поля F, то все определения и факты, приведенные выше, сохранили бы силу.

В теории кодирования важную роль играет случай, когда поле F поле вычетов Z_p, которое, как мы знаем, конечно. В этом случае соответствующее n-мерное пространство также конечно и содержит, как нетрудно видеть, р n элементов.

Понятие пространства, как и понятия группы и кольца, допускает также и аксиоматическое определение. За подробностями мы отсылаем Питателя к любому курсу линейной алгебры.

10. Лінійна комбінація. Лінійно залежні та незалежні системи векторів.

Источник

Метод Гаусса приведения матрицы к ступенчатому виду

Элементарными преобразованиями матрицы называются следующие ее преобразования:

I. Перестановка двух столбцов (строк) матрицы.

II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля.

III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.

Элементарные преобразования применяются для упрощения матриц, что будет в дальнейшем использоваться для решения разных задач.

Алгоритм приведения матрицы к ступенчатому виду

Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия.

1. В первом столбце выбрать элемент, отличный от нуля ( ведущий элемент ). Строку с ведущим элементом ( ведущая строка ), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые.

2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить.

3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа).

4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы.

Пример 1.29. Привести к ступенчатому виду матрицы

Прибавим ко второй строке первую, умноженную на (-2):

Первый столбец и первую строку исключаем из рассмотрения. В оставшейся части матрицы имеется один элемент (-2), который выбираем в качестве ведущего. Разделив последнюю строку на ведущий элемент, получаем матрицу ступенчатого вида

Преобразования закончены, так как ведущая строка последняя. Заметим, что получившаяся матрица является верхней треугольной.

Пункт 3 алгоритма делать не надо, так как под ведущим элементом стоит нуль. Исключаем из рассмотрения первую строку и первый столбец. В оставшейся части ведущий элемент — число 2. Разделив ведущую строку (вторую) на 2, получаем ступенчатый вид:

Преобразования закончены, так как ведущая строка последняя.

Ко второй и третьей строкам прибавим первую, умноженную на (-3) и на (-6) соответственно:

Обратим внимание на то, что полученная матрица еще не является матрицей ступенчатого вида, так как вторую ступеньку образуют две строки (2-я и 3-я) матрицы. Исключив 1-ю строку и 1-й столбец, ищем в оставшейся части ведущий элемент. Это элемент (-1). Делим вторую строку на (-1), а затем к третьей строке прибавляем ведущую (вторую), умноженную на 5:

Исключим из рассмотрения вторую строку и второй столбец. Поскольку исключены все столбцы, дальнейшие преобразования невозможны. Полученный вид — ступенчатый.

1. Говорят, что матрица имеет ступенчатый вид также и в случае, когда на месте ведущих элементов (обозначенных на рис. 1.4 единицей) стоят любые отличные от нуля числа.

2. Считается, что нулевая матрица имеет ступенчатый вид.

Пример 1.30. Привести к ступенчатому виду матрицу

Решение. Первый столбец матрицы — нулевой. Исключаем его из рассмотрения и исследуем оставшуюся часть (последние 5 столбцов):

Вторую строку и четвертый столбец исключаем из рассмотрения. Берем элемент в качестве ведущего. Делим третью строку на число 2 (умножаем на 0,5):

К четвертой строке прибавляем третью, умноженную на (-2):

Третью строку и четвертый столбец исключаем из рассмотрения. Поскольку в оставшейся части матрицы все элементы (один) нулевые, преобразования закончены. Матрица приведена к ступенчатому виду (см. рис. 1.4).

Замечание 1.9. Продолжая выполнять элементарные преобразования над строками матрицы, можно упростить ступенчатый вид, а именно привести матрицу к упрощенному виду (рис. 1.5).

Здесь символом 1 обозначены элементы матрицы, равные единице, символом * — обозначены элементы с произвольными значениями, остальные элементы матрицы нулевые. Заметим, что в каждом столбце с единицей остальные элементы равны нулю.

Пример 1.31. Привести к упрощенному виду матрицу

Решение. Матрица имеет ступенчатый вид. Прибавим к первой строке третью, умноженную на (-1), а ко второй строке третью, умноженную на (-2):

Теперь к первой строке прибавим вторую, умноженную на (-1). Получим матрицу упрощенного вида (см. рис. 1.5):

Замечание 1.10. При помощи элементарных преобразований (строк и столбцов) любую матрицу можно привести к простейшему виду (рис. 1.6).

Пример 1.32. Привести матрицу к простейшему виду.

Умножим все элементы последнего столбца на (-1) и переставим его на место второго:

Таким образом, исходная матрица при помощи элементарных преобразований приведена к простейшему виду (см. рис. 1.6).

Свойства элементарных преобразований матриц

Следствие (о приведении матрицы к простейшему виду). Любую матрицу при помощи элементарных преобразований ее строк и столбцов можно привести к простейшему виду.

2. В теореме 1.1 говорится о приведении матрицы к ступенчатому (упрощенному) виду при помощи элементарных преобразований только ее строк, не используя преобразования ее столбцов. Чтобы привести произвольную матрицу к простейшему виду (следствие теоремы 1.1), нужно использовать преобразования и строк, и столбцов матрицы.

3. Рассмотрим следующую модификацию пункта 3 метода Гаусса. Ведущий элемент, выбранный в п. 1 метода Гаусса, определяет ведущую строку и ведущий столбец матрицы (он находится на их пересечении). Делим все элементы ведущей строки на ведущий элемент (см. п.2 метода Гаусса). Прибавляя ведущую строку, умноженную на соответствующие числа, к остальным строкам матрицы (аналогично п.3 метода Гаусса), делаем равными нулю все элементы ведущего столбца, за исключением ведущего элемента. Затем, прибавляя полученный ведущий столбец, умноженный на соответствующие числа, к остальным столбцам матрицы, делаем равными нулю все элементы ведущей строки, за исключением ведущего элемента. При этом получаем ведущие строку и столбец, все элементы которых равны нулю, за исключением ведущего элемента, равного единице.

Источник

Матрицы: метод Гаусса. Вычисление матрицы методом Гаусса: примеры

Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.

Основные понятия

Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.

Вам будет интересно: Закон Максвелла. Распределение Максвелла по скоростям

Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.

Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.

Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.

Ступенчатый вид матрицы

Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l Понравилась статья? Поделись с друзьями:

Источник

Электронная библиотека

3. После (n-1)-го шага получаем верхнюю треугольную матрицу U и преобразованный вектор правой части. Выполняем обратную подстановку.

Метод Гаусса с частичным выбором ведущего элемента в отсутствие ошибок округления для невырожденных матриц позволяет получить точное решение, а для вырожденных матриц – сообщение о том, что матрица вырождена.

Решить систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента.

Рассмотрим ту же систему линейных уравнений, что и в предыдущих примерах.

Прямой ход метода Гаусса

Прежде всего, выбираем максимальный по модулю элемент в первом непреобразованном столбце:

Рассмотрим следующий непреобразованный столбец:

Умножим второе уравнение на 0.4 и прибавим к третьему. Получим:

Мы получили систему линейных уравнений с верхней треугольной матрицей.

Ведущими элементами являются числа: 10, 2.5, 6.2, все они по модулю больше 1, следовательно, алгоритм является вычислительно устойчивым.

В методе Гаусса с частичным выбором ведущего элемента, в отличие от метода Гаусса без выбора ведущего элемента, в случае необходимости меняются местами уравнения системы линейных уравнений. За счет этого не возникает проблем, если у невырожденной матрицы какой-либо из главных миноров равен нулю.

Рассмотрим метод Гаусса с частичным выбором ведущего элемента с точки зрения операций над матрицами.

Произвольная невырожденная матрица перестановкой строк (столбцов) может быть приведена к матрице с главными минорами, отличными от нуля ( , где P – матрица перестановок).

Матрица Р получается из единичной матрицы перестановкой строк (столбцов).

Сложность метода Гаусса с частичным выбором ведущего элемента

Метод Гаусса с частичным выбором ведущего элемента является устойчивым, если все ведущие элементы по модулю больше единицы.

Следует отметить, что метод Гаусса с частичным выбором ведущего элемента – это основной алгоритм вычислительной математики линейной алгебры.

Метод Гаусса с полным выбором ведущего элемента отличается от метода Гаусса с частичным выбором ведущего элемента тем, что на каждом шаге прямого хода ведущий элемент ищется в непреобразованной части матрицы. Непреобразованная часть матрицы – это квадратная матрица размерности n-i+1, получаемая вычеркиванием первых i – 1 строк и первых i – 1 столбцов. В методе Гаусса с полным выбором ведущего элемента возможна не только перестановка строк матрицы и соответствующих элементов правой части, но и перестановка столбцов матрицы и, соответственно, изменение порядка следования неизвестных.

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Источник

Что такое ведущий элемент в матрице

— -матрица над полем . Ведущим элементом строки матрицы называется первый (считая слева направо) ненулевой элемент строки. Столбец матрицы называется основным, если он содержит ведущий элемент какой-либо строки матрицы.

ОПРЕДЕЛЕНИЕ. Матрица А называется ступенчатой, если она удовлетворяет условиям:

(1) нулевые строки матрицы (если они есть) расположены ниже всех ненулевых строк;

(2) если — ведущие элементы ненулевых строк матрицы, то

Примеры ступенчатых матриц: 1) нулевая матрица, 2) однострочная матрица, 3) единичная матрица, 4) верхнетреугольная матрица

Над системой вектор-строк (столбцов) данной матрицы можно проводить элементарные преобразования.

ОПРЕДЕЛЕНИЕ. Элементарные преобразования над системой строк (столбцов) матрицы называются элементарными преобразованиями матрицы. Две матрицы называются строчечно-эквивалентными, если одна получается из другой при помощи цепочки элементарных преобразований над строками.

Отношение строчечной эквивалентности рефлексивно, симметрично и транзитивно, т. е. является отношением эквивалентности.

ОПРЕДЕЛЕНИЕ. Строчечным рангом матрицы называется ранг системы ее строк. Столбцовым рангом матрицы называется ранг системы ее столбцов.

Из этого определения в силу теоремы 1.8 следует предложение 3.1.

ПРЕДЛОЖЕНИЕ 3.1. Если одна матрица получается из другой в результате цепочки элементарных преобразований над строками, то строчечные ранги этих матриц равны.

ТЕОРЕМА 3.2. Любая -матрица строчечно эквивалентна ступенчатой -матрице.

Доказательство (проводится индукцией по числу строк матрицы). Если число строк матрицы равно единице, то матрица ступенчатая. Предполагая, что теорема верна для матриц с строками, докажем, что тогда она верна для матриц с строками. Пусть А есть -строчная матрица:

Если в первом столбце матрицы есть элемент, отличный от нуля, то строку с этим ненулевым элементом можно переставить с первой строкой. Легко показать, что перестановка строк — результат цепочки элементарных преобразований над строками. Поэтому будем считать, что . Матрицу А можно преобразовать в матрицу В:

при помощи цепочки элементарных преобразований. Для этого первую строку матрицы А надо умножить на Затем полученную первую строку, умноженную на прибавить к строке для .

Матрица, полученная из матрицы В вычеркиванием первой строки, содержит строк и, по индуктивному предположению, строчечно эквивалентна некоторой ступенчатой -матрице С:

На основании этого и строчечной эквивалентности матриц А и В заключаем, что матрица А строчечно эквивалентна ступенчатой матрице С:

Матрица С — ступенчатая, потому что матрица С является ступенчатой.

Если первый столбец или несколько первых столбцов матрицы — нулевые, то рассмотрим матрицу, получающуюся в результате вычеркивания этих столбцов. Эта матрица содержит в первом столбце ненулевой элемент. Поэтому из первой части доказательства следует, что она строчечно эквивалентна ступенчатой матрице. Легко видеть, что, приписав слева к этой ступенчатой матрице вычеркнутые прежде нулевые столбцы, получим матрицу, строчечно эквивалентную исходной матрице .

ТЕОРЕМА 3.3. Строчечный ранг ступенчатой матрицы равен числу ее ненулевых строк.

Доказательство. Теорема, очевидно, верна для нулевой матрицы. Предположим, что — ступенчатая матрица с ненулевыми строками. Для удобства записи будем считать, что ведущие элементы матрицы расположены в первых столбцах, т. е.

где для Таким образом, первые строк матрицы ненулевые, а остальные (если они есть) — нулевые.

Покажем, что строки линейно независимы. Надо показать, что для любых скаляров из равенства

Так как то из (1) следуют равенства

Поскольку при , из (3) следуют равенства (2). Таким образом, система ненулевых строк матрицы А линейно независима. Следовательно, строчечный ранг матрицы А равен . В общем случае доказательство проводится аналогично.

На основании теоремы 3.3 приходим к следующему правилу вычисления ранга матрицы. Для вычисления строчечного ранга матрицы А надо привести ее к ступенчатому виду С при помоьци цепочки элементарных преобразований над строками. Число ненулевых строк матрицы С равно строчечному рангу матрицы А.

Источник