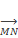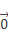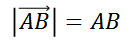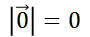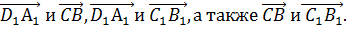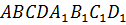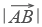Что такое векторы видеоурок
Что такое векторы видеоурок
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В геометрии очень часто мы пользуемся отрезками различной длины.
Отрезок – это часть прямой, ограниченная двумя точками.
Можно ли назвать эти точки началом и концом отрезка?
Ответом на этот вопрос будет определение, что такое вектор.
Однако для того, что бы дать это определение, рассмотрим отрезок более подробно.
Произвольный отрезок имеет два конца.
Концы отрезка также называют граничными точками.
На отрезке можно указать два направления: от одной граничной точки к другой и наоборот.
Чтобы выбрать одно из этих направлений, одну граничную точку отрезка назовём началом отрезка, а другую – концом отрезка и будем считать, что отрезок направлен от начала к концу.
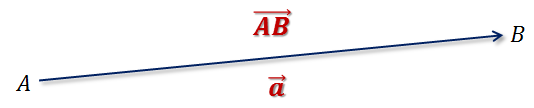
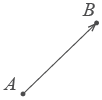
Таким образом, отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором.
На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными буквами со стрелкой над ними.
Первая буква – начало вектора, вторая – конец. Также вектор может обозначаться и одной строчной латинской буквой.
Кроме отрезка, вектором может быть любая точка плоскости.
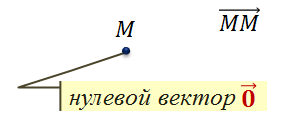
В этом случае вектор называется нулевым.
Начало нулевого вектора совпадает с его концом.
Например, на плоскости выбрана точка М, тогда нулевой вектор в этой точке будет обозначен как:
Нулевой вектор также обозначается символом, отображающим цифру ноль со стрелочкой над ним:
Теперь рассмотрим понятие длины вектора.
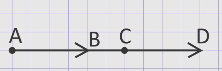
Рассмотрим два вектора АВ и СD, расположенные на одной прямой.
Эти векторы могут быть направлены либо в одну и ту же сторону, либо их направление противоположно. Данные ненулевые векторы, расположенные на одной или параллельных прямых, называются коллинеарными.
Нулевой вектор считается коллинеарным любому вектору.
Коллинеарные векторы обладают рядом свойств.
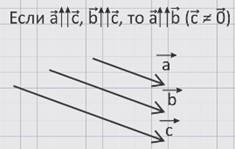
Рассмотрим три ненулевых коллинеарных вектора а, в, и с.
Если вектор а сонаправлен с вектором с и вектор в сонаправлен с вектором с, то векторы а и в также имеют одно направление – данное утверждение является первым свойством коллинеарных векторов.
Если вектор а противоположно направлен вектору с и вектор в противоположно направлен вектору с, то векторы а и в сонаправленные.
Коллинеарных векторов говорит о том, что если векторы а и с сонаправлены, а вектор в противоположно направлен с вектором с, то векторы а и в противоположно направленные.
Итак, подведем итоги урока:
Вектор – это отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом. Векторы обозначают двумя заглавными буквами со стрелкой над ними. Любую точку плоскости можно считать нулевым вектором. Длиной вектора называется длина соответствующего отрезка; ненулевые векторы, которые лежат на одной прямой или параллельных прямых, называются коллинеарными. Если два вектора сонаправлены и их длины равны, то такие векторы называются равными.
Видеоурок «Понятие вектора. Равенство векторов»
§ 1 Понятие вектора
В геометрии очень часто мы пользуемся отрезками различной длины.
Отрезок – это часть прямой, ограниченная двумя точками.
Можно ли назвать эти точки началом и концом отрезка?
Ответом на этот вопрос будет определение, что такое вектор.
Однако для того, что бы дать это определение, рассмотрим отрезок более подробно.
Произвольный отрезок имеет два конца.
Концы отрезка также называют граничными точками.
На отрезке можно указать два направления: от одной граничной точки к другой и наоборот.
Чтобы выбрать одно из этих направлений, одну граничную точку отрезка назовём началом отрезка, а другую – концом отрезка и будем считать, что отрезок направлен от начала к концу.
Таким образом, отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором.
На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают двумя заглавными буквами со стрелкой над ними.
Первая буква – начало вектора, вторая – конец. Также вектор может обозначаться и одной строчной латинской буквой.
Кроме отрезка, вектором может быть любая точка плоскости.
В этом случае вектор называется нулевым.
Начало нулевого вектора совпадает с его концом.
Например, на плоскости выбрана точка М, тогда нулевой вектор в этой точке будет обозначен как:
Нулевой вектор также обозначается символом, отображающим цифру ноль со стрелочкой над ним:
§ 2 Равенство векторов
Теперь рассмотрим понятие длины вектора.
Рассмотрим два вектора АВ и СD, расположенные на одной прямой.
Эти векторы могут быть направлены либо в одну и ту же сторону, либо их направление противоположно. Данные ненулевые векторы, расположенные на одной или параллельных прямых, называются коллинеарными.
Нулевой вектор считается коллинеарным любому вектору.
Коллинеарные векторы обладают рядом свойств.
Рассмотрим три ненулевых коллинеарных вектора а, в, и с.
Если вектор а сонаправлен с вектором с и вектор в сонаправлен с вектором с, то векторы а и в также имеют одно направление – данное утверждение является первым свойством коллинеарных векторов.
Если вектор а противоположно направлен вектору с и вектор в противоположно направлен вектору с, то векторы а и в сонаправленные.
Коллинеарных векторов говорит о том, что если векторы а и с сонаправлены, а вектор в противоположно направлен с вектором с, то векторы а и в противоположно направленные.
§ 3 Краткие итоги урока
Итак, подведем итоги урока:
Вектор – это отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом. Векторы обозначают двумя заглавными буквами со стрелкой над ними. Любую точку плоскости можно считать нулевым вектором. Длиной вектора называется длина соответствующего отрезка; ненулевые векторы, которые лежат на одной прямой или параллельных прямых, называются коллинеарными. Если два вектора сонаправлены и их длины равны, то такие векторы называются равными.
Понятие вектора
Урок 32. Геометрия 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Понятие вектора»
Вы уже знакомы с векторами из курса планиметрии. Но, так как мы приступили к изучению стереометрии, то теперь из плоскости выходим в пространство. Сразу стоит отметить, что понятие вектора в пространстве вводится также как и на плоскости.
Отрезок, для которого указано, какой из его концов является началом, а какой — концом, называется вектором. При этом направление отрезка указывается стрелкой.
Есть два способа обозначения векторов: двумя заглавными латинскими буквами со стрелкой над ними, где первая буква указывает на начало вектора, а вторая на конец; а так же одной строчной латинской буквой со стрелкой над ней.
Любая точка пространства также является вектором. Такой вектор называют нулевым. Так как у него начало совпадает с концом, то он не имеет конкретного направления.
В данном случае изображен нулевой вектор ММ.
Длина ненулевого вектора АB равна длине отрезка АB. А длина нулевого вектора всегда равна нулю.
Точно также как и на плоскости, векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными. При этом нулевой вектор коллинеарен любому вектору.
Если коллинеарные векторы имеют одинаковое направление, то их называют сонаправленными.
Если же векторы имеют противоположные направления, то их называют противоположно направленными.
Из-за того что нулевой вектор не имеет определённого направления, он является сонаправленным с любым вектором.
В данном случае сонаправленными будут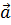 
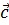
и 
. А также нулевой вектор будет сонаправлен каждому из данных векторов.
Сонаправленность векторов обозначают таким символом ↑↑.
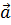
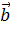
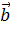
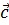
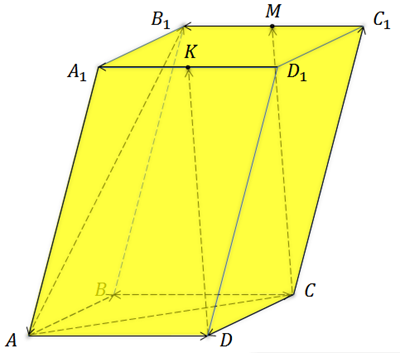
Противоположно направленными в нашем случае будут и 
, а также и . Противоположно направленные векторы обозначают таким символом ↑↓.
Выполним задание. ABCDA1B1C1D1 — параллелепипед, в котором точки М и K середины сторон B1C1 и A1D1 соответственно.
Среди векторов, изображённых на рисунке, нам предстоит найти пары сонаправленных и противоположно направленных векторов.
Итак, перед нами параллелепипед. А это значит, что все грани данного многогранника являются параллелограммами. И рёбра AA1, BB1, CC1 и DD1 параллельны. А на них изображены векторы 
и 
. Не вызывает сомнений, что они коллинеарны. И так как они направлены в противоположные стороны, то являются противоположно направленными.
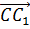
Так же параллельными будут ребра AD, BC, A1D1 и B1C1. Среди векторов, проведённых на этих рёбрах, сонаправленными будут 
Вектор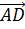 
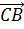
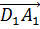
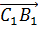
будет противоположно направленным к векторам 
, 
и 
.
Параллельными также будут рёбра AB, CD, A1B1 и C1D1. На них изображены векторы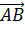 
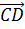
и 
. По рисунку понятно, что они противоположно направлены.
Среди четырёх оставшихся векторов коллинеарными будут только векторы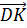 
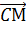
и 
. Они же будут и сонаправленными.
Так мы с вами нашли 4 пары сонаправленных векторов и 5 пар противоположно направленных векторов.
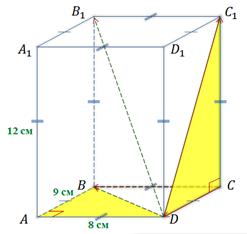
Задача.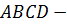 
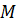
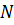
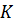
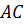
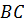
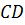
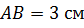
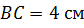
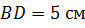
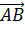
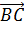
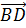
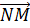
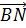
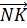
тетраэдр. Точки 
, 
и 
являются серединами сторон 
, 
и 
.
, 
, а 
. Определить длины векторов:
а) , 
, 
, 
, 
, 
;
б) ,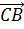 
, 
, 
, 
.
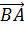
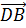
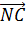
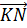
Запишем ответ.
Выполним последнее задание.
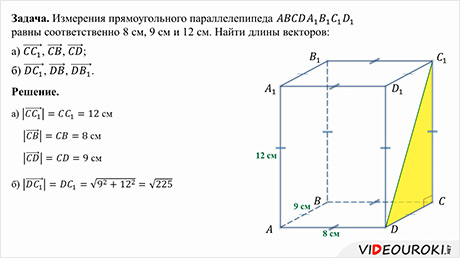
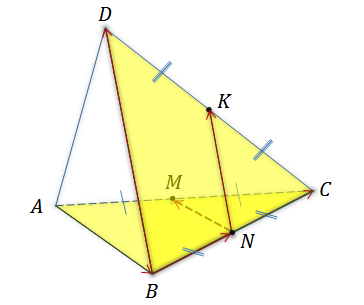
Задача. Измерения прямоугольного параллелепипеда 
равны соответственно 8 см, 9 см и 12 см. Найти длины векторов:
а) , , ;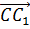
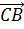
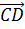
б)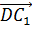 
, , 
.
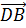
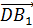
Ответ. 12 см, 8 см, 9 см; 15 см,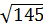 
см, 17 см.
Подведём итоги нашего урока.
Сегодня, основываясь на знаниях о векторах из курса планиметрии, мы ввели понятие вектора в пространстве.
Отрезок, для которого указано, какой из его концов является началом, а какой — концом, называется вектором. Любая точка плоскости также является вектором, нулевым вектором.
Длина ненулевого вектора AB равна длине отрезка AB. Длина нулевого вектора равна нулю.
Векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными. При этом, если они одинаково направлены, то их называют сонаправленными. Если же коллинеарные векторы противоположно направлены, то их называют противоположно направленными.
Все эти знания мы с вами смогли применить при решении задач.
Векторы
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: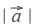 
или 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.