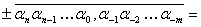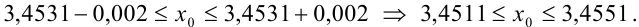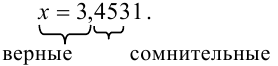Что такое верные и сомнительные цифры

Что такое верные и сомнительные цифры

Формы записи приближенных чисел

Приближенные числа записываются либо в виде конечных десятичных дробей, либо в виде целых чисел.

Замечание 1. Определение естественной (позиционной, с фиксированной точкой) формой записи целого числа дается аналогично.

В связи с этим имеет место следующее определение.

Определение 2. Значащими цифрами приближенного числа называются все цифры его записи, начиная с первой ненулевой слева.

Пример 4. У числа 0,0046 только две значащих цифры: 4 и 6.

Пример 5. У числа 0,004600 четыре значащих цифры: 4, 6 и два последних нуля. (Для чего оставляют нули в конце числа, будет рассмотрено позднее).

Если приходится работать с большим количеством приближенных чисел, то запись 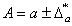не удобна. Поэтому решено было установить такой способ записи приближенных чисел, чтобы по самой этой записи можно было судить об их абсолютной (предельной абсолютной) погрешности.

Определение 4. Цифра приближенного числа называется верной в узком смысле, если абсолютная (предельная абсолютная) погрешность этого числа не превосходит половины единицы десятичного разряда, соответствующего этой цифре, в противном случае сомнительной в узком смысле.

В связи с рассмотренным примером возникает следующий вопрос: «Как отличить приближенное число 34200 с двумя последними сомнительными нулями от точного числа 34200?»

Источник

1. Теория погрешностей

Как правило, методами вычислительной математики строится приближенное решение задачи, поэтому возникает вопрос об оценке погрешности. То есть насколько сильно найденное нами приближенное решение отличается от точного решения.

Основной вопрос вычислительной математики – это вопрос о погрешности полученного числового результата.

В процессе решения задач вычислительной математики возникают следующие погрешности:

погрешность математической модели и погрешность исходных данных;

погрешность численного метода;

погрешность вычислений на ЭВМ.

Рекомендуемая литература: /3,5,6/.

1.1. Абсолютная и относительная погрешности

Приближенным числом a называется число, незначительно отличающееся от точного числа a₀ и заменяющее его в расчетах. Модуль разности между ними: 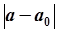– погрешность приближенного числа a.

Отметим, что число a₀ нам не известно и погрешность приближенного числа мы вычислить не можем. Для оценки погрешности вводятся абсолютная и относительная погрешности.

Абсолютной погрешностью приближенного числа a называется величина Da, удовлетворяющая неравенству .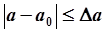

Относительной погрешностью da приближенного числа a называется отношение абсолютной погрешности Da к абсолютной величине числа a, то есть:

.

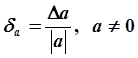
Относительная погрешность обычно выражается в процентах: da´100 %.

Абсолютная и относительная погрешности указываются в записи чисел следующим образом: .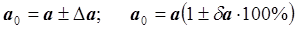

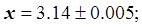
x = 3.14 (1 ± 0.005%).

1.2. Верные значащие цифры числа

Значащие цифры десятичного числа – это все его цифры, начиная с первой ненулевой слева.

x = 0.002036, цифры 2036 являются значащими;

x = 2270000, все цифры этого числа являются значащими.

Значащая цифра в записи числа верна, если абсолютная погрешность числа меньше или равна пяти единицам разряда, следующего за этой цифрой.

Определить, сколько верных значащих цифр содержит число:

x = 0.002306 ± 0.00001.

Для определения числа верных значащих цифр запишем x и Dx таким образом, чтобы легко было сравнить разряды этих чисел:

x = 0.002306, абсолютная погрешность Dx = 0.00001.

Третья значащая цифра (0) не может быть верной, так как она одного порядка с погрешностью. Верными могут быть цифры, которые стоят перед ней (2, 3). Цифра 3 будет верной, если Dx £ 0.00005. В нашем случае это условие выполнено, следовательно, 2, 3 – верные значащие цифры.

Цифры в записи числа, следующие за верными, называются сомнительными.

В числе x = 1.121 три верные значащие цифры (1, 1, 2) и одна сомнительная (1).

x = 0.002306 ± 0.00007;

В числе x = 0.002306 одна верная значащая цифра (2), три сомнительные (3, 0, 6).

В числе x = 12.3 три значащие цифры, две верные значащие цифры (1, 2), одна сомнительная (3).

В числе x = 12.3 одна верная значащая цифра (1), две сомнительные (2, 3).

При записи абсолютной и относительной погрешностей используют, как правило, одну-две значащие цифры. Приближенные числа принято записывать следующим образом: сначала записывают все верные значащие цифры, затем одну-две сомнительные. То есть в записи приближенного числа, как правило, число значащих цифр на одну-две больше, чем число верных значащих цифр.

Практическое правило. Одна верная значащая цифра в записи числа соответствует приблизительно относительной погрешности 10 %. И наоборот, относительная погрешность 10 % соответствует приблизительно одной верной значащей цифре. Две верные значащие цифры соответствуют относительной погрешности 1 %, три верные значащие цифры – относительной погрешности 0.1 %.

1.3. Особенности математических вычислений на ЭВМ

ЭВМ – это машина с конечной памятью, состоящей из слов конечной длины. Возникает проблема представления бесконечного множества чисел конечным множеством чисел, представимых в ЭВМ.

Источник

Запись приближенных чисел. Верные и значащие цифры

Создатель теории приближенных вычислений А. Н. Крылов говорил: «При производстве всяких численных вычислений надо руководствоваться правилом: точность вычислений должна соответствовать точности данных и той практической потребности, для которой вычисления производятся». Ему же принадлежат слова: «Помните, что каждая неверная цифра — это ошибка, всякая лишняя цифра — это пол-ошибки».

Приближенные числа записываются, как правило, при помощи десятичных дробей. Между записью приближенных и точных чисел есть различия. Если перед нами точное число, то вес его цифры являются верными, точными. Что же касается приближенного числа, то некоторые его цифры верны, а другие являются сомнительными.

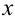
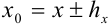
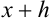
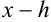
Цифра десятичного разряда приближенного числа приближения называется верной, если в том же десятичном разряде чисел и стоит эта же цифра. В противном случае она называется сомнительной.

Проверку на верные и сомнительные цифры нужно начинать слева направо с наивысшего разряда. Все цифры, стоящие правее первой найденной сомнительной цифры, автоматически считаются сомнительными.

Пример №45.4.

Найдите верные и сомнительные цифры в записи числа .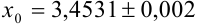

Решение:

Поскольку 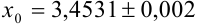, запишем диапазон возможных значений в виде двойного неравенства:

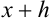
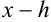
Начинаем проверку на верные и сомнительные цифры с наивысшего разряда — единиц. Видим, что цифры 3,45 одинаковы в левой и правой части двойного неравенства (т.е. в записи и ), следовательно, по определению в записи приближенного числа 3,4531 эти цифры являются верными.

Цифры в разряде тысячных в правой и левой части двойного неравенства отличаются (1 и 5), следовательно, в записи приближенного числа 3,4531 цифра 3, стоящая в разряде тысячных, и цифра 1, стоящая за ней, являются сомнительными.

Итак, точное число обязательно начинается с цифр 3,45. Какие цифры стоят в остальных разрядах числа, точно сказать невозможно.

Для записи приближенных чисел существуют следующие правила:

Проиллюстрируем применение данных правил на конкретных примерах.

1. Поскольку в записи числа следует оставлять только верные цифры, то в примере 45.4 точное значение будет записано следующим образом: . В этом случае граница абсолютной погрешности .

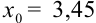
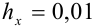
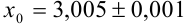
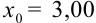
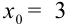
2. Если задано число , то нетрудно показать, что в записи приближенного числа 3,005 цифры 3,00 являются верными, а 5 — сомнительной. Для записи точного числа выпишем все его верные цифры, включая нули на конце: . Эта запись показывает, что граница абсолютной погрешности равна единице последнего разряда, т.е. 0,01. Если бы мы записали это число как , то граница абсолютной погрешности была бы равна 1, а это значительно более низкая точность, чем заданная в примере 0,01.

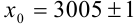
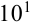
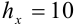
3. Пусть задано число . В записи приближенного числа 3005 цифры 300 являются верными, а 5 — сомнительной. Для записи точного числа выпишем вес его верные цифры 300, а вместо одной сомнительной цифры 5 запишем умножение на , поскольку заменяем только одну цифру. Тогда .

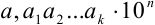
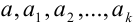
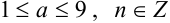
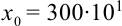
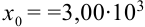
В науке принято записывать числа в стандартном виде, т.е. в виде , где — цифры, причем (в целой части числа стоит только одна цифра, отличная от нуля). Число в стандартном виде будет представлено как .

Значащими цифрами числа называют все его верные цифры, за исключением нулей, стоящих левее первой отличной от нуля цифры.

Например, число 0,712 содержит три значащие цифры: 7, 1, 2. Число 0,00012 — две значащие цифры: 1 и 2. Число 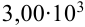— три значащие цифры: 3, 0, 0.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Приближённые вычисления в математике

Содержание:

Приближённые вычисления

Приближённые вычисления — вычисления, в которых данные и результат (или только результат) являются числами, приближенно представляющими истинные значения соответствующих величин. Числовые данные, полученные измерением реальных объектов, редко бывают точными значениями соответствующей величины, а обычно имеют некоторую погрешность

Абсолютная и относительная погрешности

При решении практических задач часто приходится иметь дело с приближёнными значениями разных числовых величин. К ним относятся: результаты измерения разных величин с помощью приборов; значения полученные при считывании на графиках, диаграммах, номограммах; проектные данные; результаты округления чисел; результаты действий над приближёнными числами; табличные значения некоторых величин; результаты вычислений значений функции. Приближённые значения (приближение, приближённые числа) могут значительно отличаться от точных, либо быть близкими к ним.

Для оценки отклонения приближённых чисел от точных используют такие понятия как абсолютная и относительная погрешности.

Абсолютной погрешностью приближённой называется модуль разности между точным значением величины и её приближённым значением х, то есть

Пример.

Абсолютная погрешность приближённого числа числом 0,44 составляет

Если точное число неизвестно, то найти абсолютную погрешность невозможно. На практике вводят оценку допустимой при данных измерениях или вычислениях абсолютной погрешности, которую называют пределом абсолютной погрешности и обозначают буквой h. Считают, что h. Как правило, предел абсолютной погрешности устанавливают из практических соображений, например, при измерениях пределом абсолютной погрешности считают наименьшее деление прибора.

При записи приближённых чисел часто используют понятия верной и сомнительной цифры.

Цифра называется верной, если предел абсолютной погрешности данного приближения не превышает единицы того разряда, в котором записана эта цифра. В другом случае цифра называется сомнительной.

Например: в числе две цифры верны, поскольку погрешность 0,04 не превышает единицу разряда десятых. Цифры 9 и 7 верны, поскольку а цифры 4 и 6 являются сомнительными, поскольку

В конечной записи приближённого числа сохраняют только верные цифры. Так число можно записать в виде , число в виде Если в десятичной дроби последние верные цифры — нули, то их оставляют в записи числа.

Например: если , то правильной записью числа будет 0,260.

Если в целом числе последние нули являются сомнительными, их исключают из записи числа.

Именно поэтому при работе с приближёнными числами широко используют стандартную форму записи числа.

Например: в числе верными являются три первые цифры, а два последних нуля — сомнительные цифры. Запись числа возможна только в виде:

Следовательно, в десятичной записи приближённого числа последняя цифра указывает на точность приближённости, то есть предел абсолютной погрешности не превышает единицу последнего разряда.

Например:

1. Запись означает, что , то есть предел абсолютной погрешности h=0,01.

2. Запись

3. Если

В десятичной записи числа значимыми цифрами называются все его верные цифры начиная с первой слева, отличной от нуля.

Например: в числе 1,13 — три значимых цифры, в числе 0,017 — две, в числе 0,303 — три, в числе 5,200 — четыре, в числе 25_*10 3 — две значимых цифры.

При таком подходе к записи приближенного числа необходимо уметь округлять числа.

Правила округления чисел:

— Если первая цифра, которую отбрасываем является меньше пяти, то в основном разряде, который сохраняется цифра не меняется. Например: 879,673≈879,67.

— Если первая цифра, которую отбрасываем больше пяти, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 456,87≈456,9.

— Если первая цифра, которая отбрасывается пять и за ней есть ещё отличны от нуля, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 1246,5002≈1247.

— Если первая цифра, которая отбрасывается — пять и за ней нет больше никаких цифра, то в последнем разряде, который сохраняется цифра увеличивается на единицу. Например: 0,275≈0,28; 1,865≈1,86.

Абсолютная погрешность не полностью характеризует точность приближения. Например, будет грубой ошибкой при измерении жука, и незначительной при измерении кита. Тоже самое можно сказать и про предел абсолютной погрешности. Качество (точность) приближённости лучше характеризуется относительной погрешностью.

Относительной погрешностью (омега) приближённости х величины называется отношением абсолютной погрешности этого приближения к модулю приближённого значения х, то есть

Поскольку абсолютная погрешность обычно бывает неизвестна, то на практике оценивают модуль относительной погрешности некоторым числом, которое не меньше чем этот модуль:

Число называется пределом относительной погрешности.

Предел относительной погрешности можно вычислить по формуле:

Конечно относительная погрешность выражается в процентах.

С помощью относительной погрешности легко установить точность приближённости.

Пример 1. Найти относительную погрешность числа

Решение: Имеем

Следовательно

Пример 2. Сравнить точность измерения толщины книги d (см) и высоты стола H (см), если известно, что .

Решение:

Как видим, точность измерения высоты стола значительно выше.

Выполнение действий над приближёнными числами

Результат арифметических действий над приближёнными числами является также приближённым числом.

Пример 3. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадрата числа 5,62 и квадратного корня из числа 18,50.

Найдём границу относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Пример 4. Вычислить приближение значения выражения и найти предел погрешностей результата.

Решение: находим значение квадратного корня из числа 6,24 и , имеем:

Граница относительной погрешности результата:

Граница абсолютной погрешности результата:

Ответ:

Выполнение действий без точного учёта погрешности

Точный учёт погрешности усложняет вычисление. Поэтому, если не надо учитывать погрешность промежуточных результатов, можно использовать более простые правила.

Сложение и вычитание приближённых вычислений рекомендуется выполнять так:

а) выделить слагаемое с наименьшим числом верных десятичных знаков;

б) округлить другие слагаемые так, чтобы каждое из них содержало на один десятичный знак больше чем выделенное;

в) выполнить действия, учитывая все сохранённые десятичные знаки;

г) результаты округлить и сохранить столько десятичных знаков, сколько их есть в приближённом числе с наименьшим числом десятичных знаков.

Умножение и деление приближённых вычислений рекомендуется выполнять так:

а) выделить среди данных чисел, число с наименьшим количеством верных значимых цифр;

б) округлить оставшиеся данные так, чтобы каждое из них содержало на одну значащую цифру больше, чем в выделенном;

в) выполнить действия — сохранить все значимые цифры;

г) сохранять в результате столько значащих цифр, сколько их имеет выделенное число с наименьшим количеством верных значимых цифр.

При возведении в степень приближённого числа в результате сохраняют столько значимых цифр, сколько верных значимых цифр имеет основа степени.

При извлечении корня из приближённого числа в результате сохраняют столько верных цифр, сколько имеет подкоренное число.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник