Что такое вершина геометрия 8 класс

Многоугольники

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :

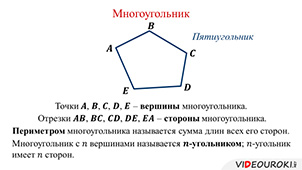
В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.

Выпуклые и вогнутые

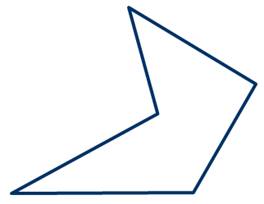
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника ABCDE равен:

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

где t — это количество треугольников, а n — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.

Источник

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

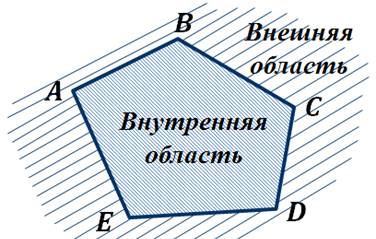
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

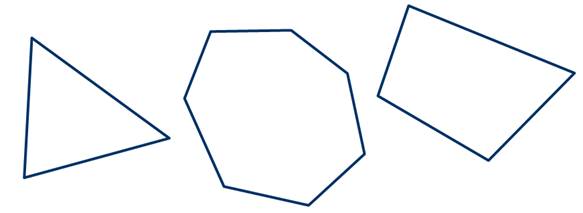
На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

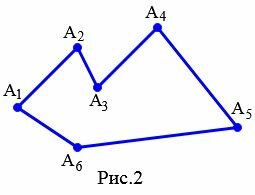На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

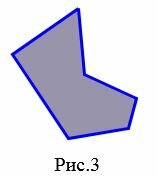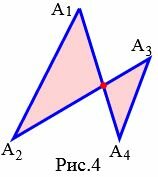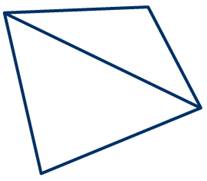
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

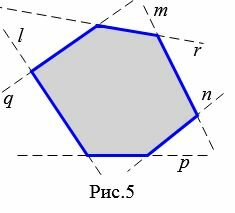На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

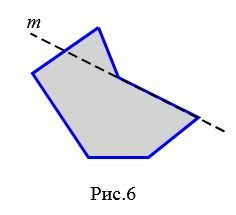На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

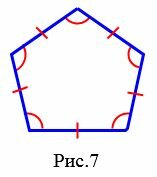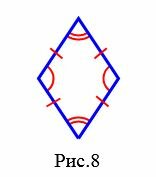На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

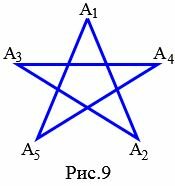На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

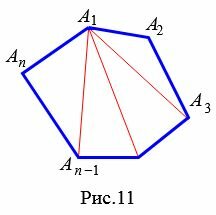Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник

Вершина (геометрия)

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.

В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.

Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.

Источник

Многоугольник

Урок 1. Геометрия 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Многоугольник»

На этом уроке мы поговорим о геометрической фигуре, которую называют многоугольником. Уже само слово «многоугольник» указывает на то, что эта фигура имеет много углов.

Давайте посмотрим на следующую фигуру, которая составлена из отрезков AB, BC, CD, DE, EA. Причем смежные отрезки, то есть отрезки AB и BC, BC И CD, CD и DЕ, DE и ЕА, ЕА и АB не лежат на одной прямой, а несмежные отрезки, например, AB и CD, BC и ED, АЕ и CD, не имеют общих точек. Такую фигуру называют многоугольником.

Точки A, B, C, D и Е называются вершинами этого многоугольника, а отрезки AB, BC, CD, DE и ЕА – его сторонами.

Периметром многоугольника называется сумма длин всех его сторон.

Обратите внимание, что рассматриваемый многоугольник имеет 5 вершин и 5 сторон, а поэтому его называют пятиугольником.

Многоугольник с n вершинами называется n-угольником. N-угольник имеет n сторон.

Треугольник является примером многоугольника. Четырёхугольник и семиугольник также являются примерами многоугольников.

А вот следующая фигура не является многоугольником, так как несмежные отрезки и имеют общую точку.

Вернёмся к многоугольнику, рассматриваемому вначале урока.

А вот отрезок, соединяющий любые две не соседние вершины, например, AC, BЕ, АD, называется диагональю многоугольника.

Многоугольник разделяет плоскость на две части, а именно, на внутреннюю область многоугольника и на внешнюю.

Следует отметить, что многоугольником также называют фигуру, состоящую из отрезков и внутренней области.

Все многоугольники делят на выпуклые и невыпуклые. Многоугольник называется выпуклым, если он лежит по одну сторону от прямой, проходящей через любые две соседние вершины.

А вот если многоугольник лежит по разные стороны хотя бы от одной прямой, проходящей через две соседние вершины, то его называют невыпуклым.

Теперь давайте выясним, чему же равна сумма углов выпуклого n-угольника.

Давайте возьмём выпуклый четырёхугольник и проведём в нем диагональ, Получили два треугольника.

Мы знаем, что сумма углов треугольника равна ста восьмидесяти градусам. А тогда сумма углов выпуклого четырёхугольника равняется сумме углов этих двух треугольников, то есть равняется 180º умножить на 2 и равняется 360º.

Теперь возьмем выпуклый пятиугольник и, проведя в нём две диагонали, разобьём его на три треугольника.

Тогда сумма углов выпуклого пятиугольника равняется .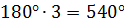

И возьмем еще, например, выпуклый шестиугольник. Проведём в нем три диагонали.

И получим четыре треугольника. А тогда сумма углов выпуклого шестиугольника будет равна .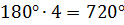

Таким образом, мы могли бы продолжать находить суммы углов других выпуклых многоугольников. Но обратите внимание, что в четырёхугольнике четыре стороны и мы его разбили на два треугольника. В пятиугольнике: пять сторон – три треугольника. А в шестиугольнике: шесть сторон – четыре треугольника

То есть в каждом случае получается, что треугольников на два меньше, чем сторон у рассматриваемой фигуры.

На основании этого сделаем вывод: сумма углов выпуклого n-угольника равна 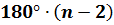, где n – количество сторон (углов).

А теперь давайте решим несколько задач.

Задача. Найти сумму углов выпуклого: а) пятиугольника; б) десятиугольника.

Для того чтобы найти сумму углов выпуклого пятиугольника, мы в полученное выше выражение вместо n подставим 5, выполним вычисления и получим 540º.

а) ;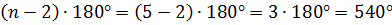

А вот чтобы найти сумму углов десятиугольника, подставим в выражение вместо n 10:

б) .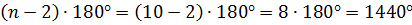

Ответ: 540 градусов, 1440 градусов.

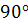
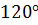
Задача. Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен: а) ; б) ?

Источник

Теория Геометрия 8 класс

1. Многоугольник — это фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.

3.Две вершины многоугольника, принадлежащие одной стороне, называются соседними.

4.Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.

5.Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

6.Сумма углов выпуклого n-угольника равна (n–2) ·180°.

7. Четырёхугольник– это многоугольник у которого четыре вершины и четыре стороны.

8.Две несмежные стороны четырёхугольника называются противоположными.

9.Две вершины, не являющиеся соседними, называются противоположными.

10. Сумма углов выпуклого четырехугольника равна 360°.

11. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

12. Свойства параллелограмма:

· В параллелограмме противоположные стороны равны и противоположные углы равны.

· Диагонали параллелограмма точкой пересечения делятся пополам.

13. Признаки параллелограмма:

· Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.

· Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

· Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

14. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.

15.Трапеция называется равнобедренной, если её боковые стороны равны.

16.Трапеция называется прямоугольной, если один из её углов прямой.

· Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

18. Прямоугольником называется параллелограмм, у которого все углы прямые.

19. Особое свойство прямоугольника:

· Диагонали прямоугольника равны.

20. Признак прямоугольника:

· Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.

21. Ромбом называется параллелограмм, у которого все стороны равны.

22. Особое свойство ромба:

· Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

23. Квадратомназывается прямоугольник, у которого все стороны равны.

24. Основные свойства квадрата:

· Все углы квадрата прямые.

· Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

25.Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему.

26.Две точки А и А₁ называются симметричными относительно точки О, если О – середина отрезка АА_1.

27. Основные свойства площадей:

· Равные многоугольники имеют равные площади.

· Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

29.Площадь прямоугольника равна произведению его смежных сторон S=ab.

30.Площадь параллелограмма равна произведению его основания на высоту S=ah.

31.Площадь треугольника равна половине произведения его основания на высоту S= 0,5ah.

32.Площадь прямоугольного треугольника равна половине произведения его катетов S= 0,5ab.

33. Если высоты двух треугольников равны, то их площади относятся как основания.

34. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

35.Площадь трапеции равна произведению полусуммы её оснований на высоту S= 0,5(а+b) · h.

36. Теорема Пифагора:

· В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. с 2 =a 2 +b 2

37. Теорема, обратная теореме Пифагора:

· Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

38.Треугольник со сторонами 3, 4, 5 называют египетским треугольником.

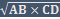
40. Говорят, что отрезки AB и CD пропорциональны отрезкам A₁B₁ и C₁D_1, если = .

41.Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

42.Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

43. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

44. Признаки подобия треугольников:

· Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

· Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

· Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

45. Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.

46. Т. о средней линии треугольника:

· Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

47. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

48. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

49.Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если XY=

50. Средняя линия трапеции — это отрезок, соединяющий середины ее боковых сторон.

51. Т. о средней линии трапеции:

· Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.

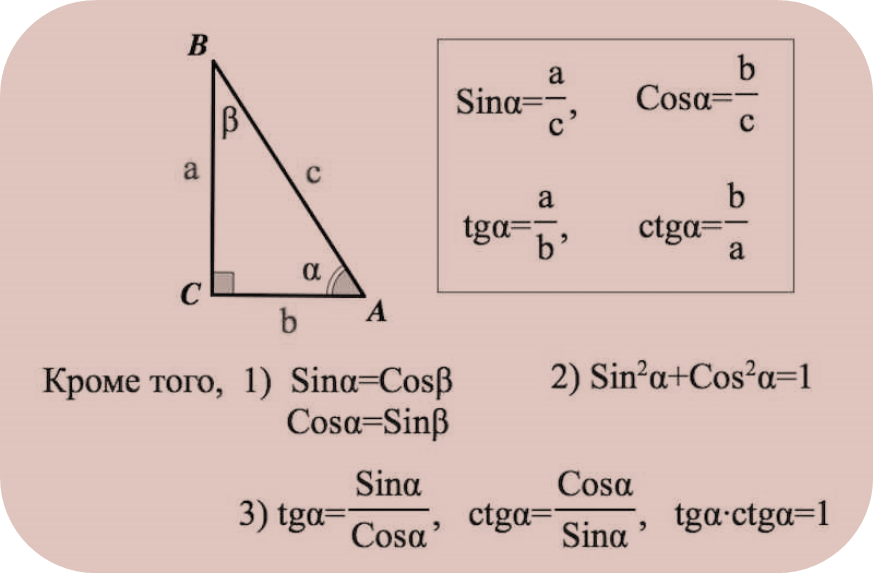
52. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

53. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

54. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

α	30 0	45 0	60 0
Синус α	0,5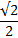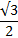
Косинус α		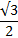	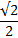0,5
Тангенс α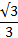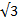
Котангенс α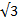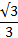

55. Тангенс угла равен отношению синуса к косинусу этого угла.

56. sin 2 A+cos 2 A=1 – основное тригонометрическое тождество.

57. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

58. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

59. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

60.Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

61. Т. о свойстве касательной к окружности:

· Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

62. Свойство отрезков касательных, проведённых из одной точки:

· Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

63. Признак касательной:

· Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

64.Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.

65.Угол с вершиной в центре окружности называется её центральным углом.

66. Центральный угол измеряется дугой, на которую он опирается.

67. Сумма градусных мер двух дуг окружности с общими концами равна 360°.

68.Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

69. Вписанный угол измеряется половиной дуги, на которую он опирается.

70. Вписанные углы, опирающиеся на одну и ту же дугу, равны.

71. Вписанный угол, опирающийся на полуокружность – прямой.

72. Теорема о произведении отрезков пересекающихся хорд:

· Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

73. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.

74. Биссектрисы треугольника пересекаются в одной точке.

75. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

76. Теорема о серединном перпендикуляре к отрезку:

· Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

· Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.

77. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

78. Высоты треугольника (или их продолжения) пересекаются в одной точке.

79. Четыре замечательные точки треугольника:

· Точка пересечения медиан.

· Точка пересечения биссектрис.

· Точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).

80.Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

81. Теорема об окружности, вписанной в треугольник:

· В любой треугольник можно вписать окружность.

· В треугольник можно вписать только одну окружность.

82. Не во всякий четырёхугольник можно вписать окружность.

83. В любом описанном четырёхугольнике суммы противоположных сторон равны.

84. Если суммы противоположных сторон выпуклого четырёхугольника равны то в него можно вписать окружность.

85.Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

86. Теорема об окружности, описанной около треугольника:

· Около любого треугольника можно описать окружность.

· Около треугольника можно описать только одну окружность.

87. Около четырёхугольника не всегда можно описать окружность.

88. В любом вписанном четырёхугольнике сумма противоположных углов равна 180°.

89. Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.

Источник