Что такое вершина пирамиды в математике

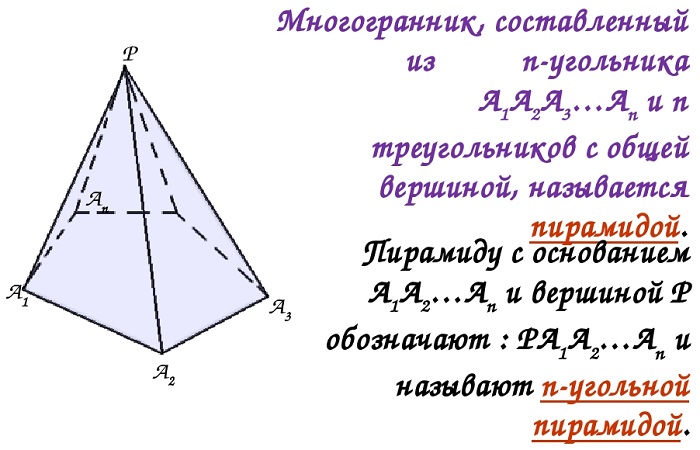
Пирамида

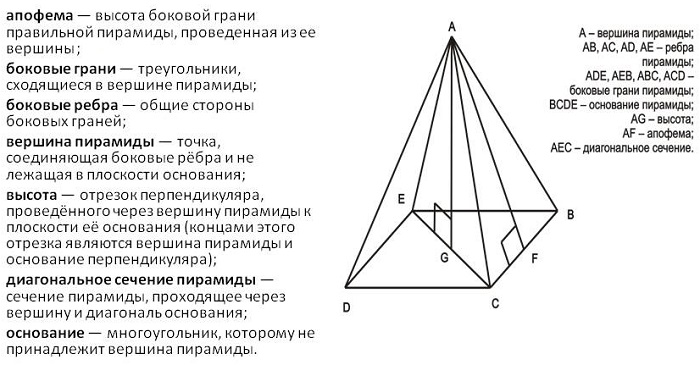
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

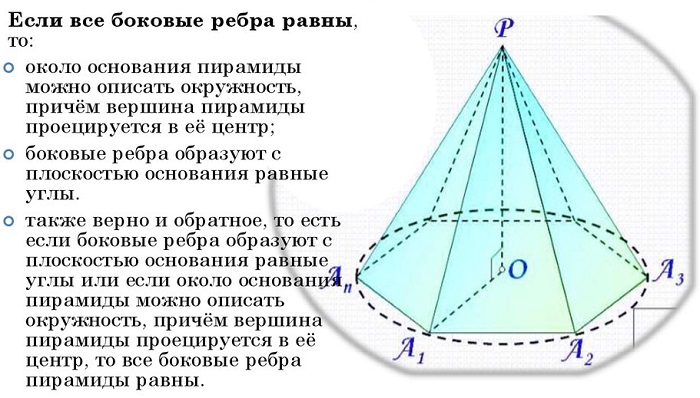
1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

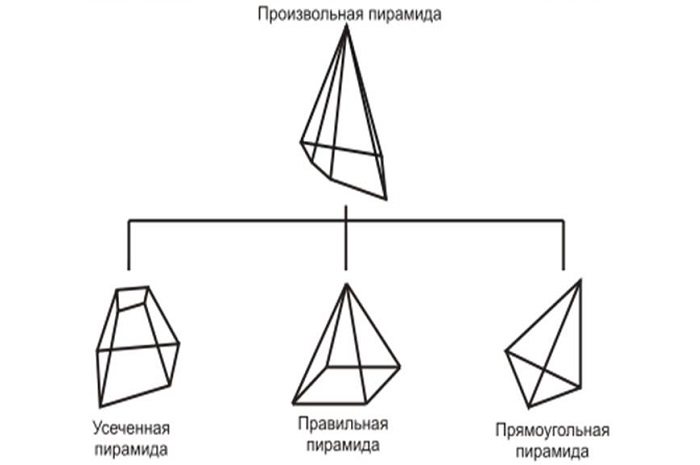
Виды пирамид

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Источник

Геометрические фигуры. Пирамида.

Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые имеют общую вершину. Пирамида – это частный случай конуса.

Элементы пирамиды.

Свойства пирамиды.

1. Когда все боковые ребра имеют одинаковую величину, тогда:

2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:

3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу.

4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.

5. Конус будет вписанным в пирамиду, когда вершины их совпадут, а основание конуса будет вписанным в основание пирамиды. При этом вписать конус в пирамиду можно лишь в том случае, если апофемы пирамиды имеют равные величины (необходимое и достаточное условие).

6. Конус будет описанным около пирамиды, если их вершины совпадут, а основание конуса будет описано около основания пирамиды. При этом описать конус около пирамиды можно лишь в том случае, если все боковые ребра пирамиды имеют одинаковые величины (необходимое и достаточное условие). Высоты у этих конусов и пирамид одинаковы.

7. Цилиндр будет вписанным в пирамиду, если 1-но его основание совпадет с окружностью, которая вписана в сечение пирамиды плоскостью, параллельной основанию, а второе основание будет принадлежать основанию пирамиды.

8. Цилиндр будет описанным около пирамиды, когда вершина пирамиды будет принадлежать его одному основанию, а второе основание цилиндра будет описано около основания пирамиды. При этом описать цилиндр около пирамиды можно лишь в том случае, если основанием пирамиды служит вписанный многоугольник (необходимое и достаточное условие).

Виды пирамид.

По количеству углов основания пирамиды делят на треугольные, четырехугольные и так далее.

Пирамида будет треугольной, четырехугольной, и так далее, когда основанием пирамиды будет треугольник, четырехугольник и так далее. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и так далее.

Источник

Что такое пирамида: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение пирамиды

Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.

Примечание: пирамида – это частный случай конуса.

Элементы пирамиды

Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.

Примечание: свойства пирамиды представлены в отдельной публикации.

Виды сечения пирамиды

1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):

2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.

Примечание: Существуют и другие виды сечения, но они не так распространены.

Источник

Объем пирамиды (ЕГЭ 2022)

В этой статье вы поймете что такое пирамида и какими они бывают.

Вы научитесь вычислять объем пирамиды, высоту и другие ее параметры.

Вы научитесь решать задачу на доказательство (ЕГЭ №14) и записывать доказательства так, чтобы не сняли баллы на ЕГЭ.

Объем пирамиды — коротко о главном

Определение пирамиды:

Пирамида – это многогранник, который состоит из любого плоского многоугольника (основание пирамиды), точки, не лежащей в плоскости основания, (вершина пирамиды) и всех отрезков, соединяющих вершину пирамиды с точками основания.

Треугольники, в которые «сливаются» эти отрезки, называются боковыми гранями, а отрезки, проведённые к вершинам основания — это боковые ребра.

Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

Правильная пирамида — пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.

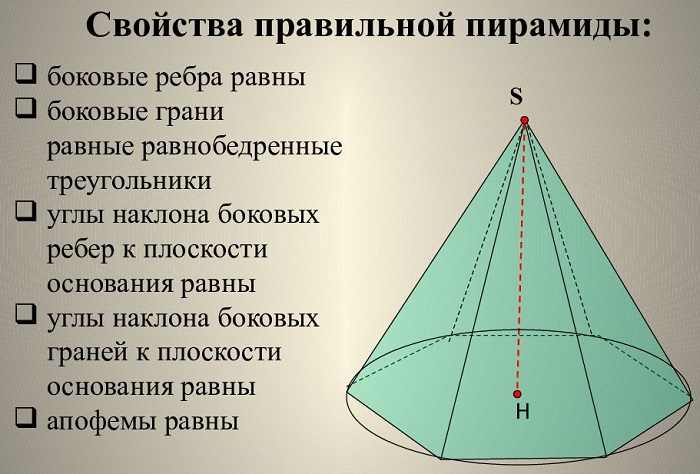
Свойства правильной пирамиды:

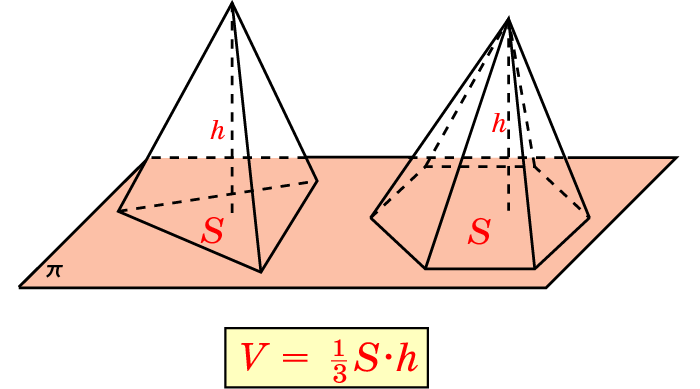
Объем пирамиды:

Что такое пирамида

Вместо того, чтобы читать длинное определение, достаточно просто посмотреть на картинку:

Видишь: у пирамиды внизу (говорят «в основании») какой-нибудь многоугольник, и все вершины этого многоугольника соединены с некоторой точкой в пространстве (эта точка называется «вершина»).

У всей этой конструкции ещё есть боковые грани, боковые рёбра и рёбра основания.

Ещё раз нарисуем пирамиду вместе со всеми этими названиями:

Некоторые пирамиды могут выглядеть очень странно, но всё равно это – пирамиды.

Вот, например, совсем «косая» пирамида.

И ещё немного о названиях: если в основании пирамиды лежит треугольник, то пирамида называется треугольной, если четырёхугольник, то четырёхугольной, а если стоугольник, то … догадайся сам.

Высота пирамиды

Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

При этом точка, куда oпустилась высота, называется основанием высоты.

Обрати внимание, что в «кривых» пирамидах высота может вообще оказаться вне пирамиды.

И ничего в этом страшного нет. Похоже на тупоугольный треугольник.

Правильная пирамида

Правильной называется такая пирамида, у которой в основании лежит правильный многоугольник, а вершина пирамиды проецируется в центр основания.

Много сложный слов?

Давай расшифруем: «В основании – правильный многоугольник» — это понятно.

А теперь вспомним, что у правильного многоугольника есть центр – точка, являющаяся центром и вписанной, и описанной окружности.

Ну вот, а слова «вершина проецируется в центр основания» означают, что основание высоты попадает как раз в центр основания. Смотри, как ровненько и симпатично выглядит правильная пирамида.

Шестиугольная правильная пирамида

В основании – правильный шестиугольник, вершина \( \displaystyle S\) проецируется в центр основания.

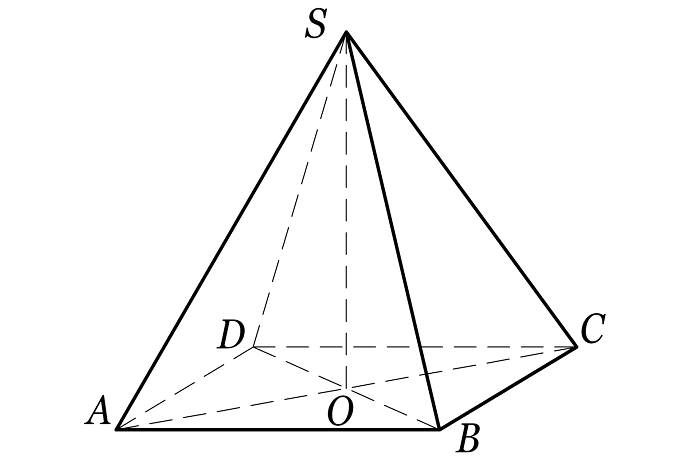
Четырехугольная правильная пирамида

В основании – квадрат, вершина \( \displaystyle S\) проецируется в точку пересечения диагоналей этого квадрата.

Треугольная правильная пирамида

В основании – правильный треугольник, вершина \( \displaystyle S\) проецируется в точку пересечения высот (они же и медианы, и биссектрисы) этого треугольника.

Очень важные свойства правильной пирамиды

В правильной пирамиде:

Объем пирамиды

Главная формула объема пирамиды

Откуда взялась именно \( \displaystyle \frac<1><3>\)?

Это не так уж просто, и на первых порах нужно просто запомнить, что у пирамиды и конуса в формуле объема есть \( \displaystyle \frac<1><3>\), а у цилиндра – нет.

Теперь давай посчитаем объем самых популярных пирамид.

Объем правильной треугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle <_<осн>>\) и \( \displaystyle H\).

\( \displaystyle <_<осн>>\) – это площадь правильного треугольника \( \displaystyle ABC\).

Вспомним, как искать эту площадь.

Используем формулу площади:

\( \displaystyle S=\frac<1><2>ab\cdot \sin \gamma \)

У нас «\( \displaystyle a\)» – это \( \displaystyle a\), а «\( \displaystyle b\)» — это тоже \( \displaystyle a\), а \( \displaystyle \sin \gamma =\sin 60<>^\circ =\frac<\sqrt<3>><2>\)

Теперь найдем \( \displaystyle H\).

По теореме Пифагора для \( \displaystyle \Delta SOC\)

Чему же равно \( \displaystyle OC\)?

Это радиус описанной окружности в \( \displaystyle \Delta ABC\), потому что пирамида правильная и, значит, \( \displaystyle O\) — центр \( \displaystyle \Delta ABC\)

Найдем \( \displaystyle OC\) (Подробнее смотри в теме «Правильный треугольник»).

\( \displaystyle OC=\frac<2><3>CK\), так как \( \displaystyle O\) — точка пересечения и медиан тоже.

\( \displaystyle C<^<2>>=A<^<2>>-A<^<2>>\) (теорема Пифагора для \( \displaystyle \Delta ACK\))

Подставим \( \displaystyle OC\) в формулу для \( \displaystyle H\).

И подставим все в формулу объема:

Внимание: если у тебя правильный тетраэдр (т.е. \( \displaystyle b=a\)), то формула получается такой:

Объем правильной четырехугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\).

Здесь \( \displaystyle <_>\) и искать не нужно; ведь в основании – квадрат, и поэтому \( \displaystyle <_>=<^<2>>\).

Найдем \( \displaystyle H\). По теореме Пифагора для \( \displaystyle \Delta SOD\)

Известно ли нам \( \displaystyle OD\)? Ну, почти. Смотри:

Подставляем \( \displaystyle OD\) в формулу для \( \displaystyle H\):

А теперь и \( \displaystyle H\) и \( \displaystyle <_>\) подставляем в формулу объема.

Объем правильной шестиугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро \( \displaystyle b\).

Как найти \( \displaystyle <_>\)? Смотри, шестиугольник \( \displaystyle ABCDEF\) состоит ровно из шести одинаковых правильных треугольников. Площадь правильного треугольника мы уже искали при подсчете объема правильной треугольной пирамиды, здесь используем найденную формулу.

Теперь найдем \( \displaystyle H\) (это \( \displaystyle SO\)).

По теореме Пифагора для \( \displaystyle \Delta SOE\)

Но чему же равно \( \displaystyle OE\)? Это просто \( \displaystyle a\), потому что \( \displaystyle \Delta EOF\) (и все остальные тоже) правильный.

Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ №14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

В этом видео мы разобрали следующие вопросы:

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

А теперь попробуй ты!

Мы рассказали тебе все о пирамидах. Не о тех, что строили инопланетяне и рептилоиды, но все же… Сделали это не хуже всяких конспирологических каналов!

Теперь ты можешь быть уверен, что у тебя есть хорошая база для решения большинства задач стереометрии. И ты не зайдешь в тупик прямо со слов «В правильном тетрадэдре PABCD…»

А теперь слово тебе. Расскажи нам, понравилась ли тебе статья? Были ли трудности?

Напиши нам ниже в комментариях!

А еще можешь задавать любые вопросы. Мы читаем все и обязательно ответим.

Источник

Пирамида является одной из основных фигур в геометрии. О её особенностях рассказано в статье.

Определение пирамиды в геометрии

Эта стереометрическая фигура включает в себя часть пространства, отделённую плоскими многоугольниками: произвольным в основании и гранями — треугольниками, содержащими общую вершину и отрезок в виде общей стороны с ним.

Элементы пирамиды

Элементами этой геометрической фигуры являются:

Место, куда сходятся все боковые грани фигуры, является вершиной.

Многоугольник, от каждой стороны которого отходят треугольные грани, носит название основания. Например, оно может быть шестиугольным.

Треугольники, соединяющиеся у вершины, с общей стороной с основанием, носят название боковых граней. У них противоположная вершина совпадает с точкой вершины пирамиды.

Высота фигуры представляет собой вертикальный отрезок, ограниченный многоугольником основания и вершиной.

На каждом треугольнике боковой стороны можно указать апофему. Она опускается от вершины по грани до ребра основания, будучи к нему перпендикулярной.

Боковыми ребрами называют те отрезки, которые соединяют соседние боковые грани.

У пирамиды может быть несколько диагональных сечений. Они включают в себя диагональ многоугольника вместе с вершиной пирамиды.

Виды пирамид

Такие фигуры могут относиться к различным видам, в зависимости от типа основания и расположения вершины.

Можно указать следующие разновидности пирамид:

Правильной она будет в том случае, если в основании лежит правильный многоугольник. Проекция вершины на многоугольник основания должна приходиться на центр. Тетраэдр рассматривается как одна из разновидностей правильной пирамиды.

У прямоугольной фигуры одна из граней находится в плоскости, перпендикулярной многоугольнику, лежащему в основании.

Усеченная — это часть фигуры, находящаяся между пересекающей плоскостью и многоугольником основания. Причём эта плоскость должна располагаться горизонтально.

Свойства пирамиды

У этой объёмной геометрической фигуры имеются следующие свойства при условии равенства боковых рёбер:

круг возможно описать вокруг многоугольника основания;

угол, под которым наклонены боковые грани, будет таким же.

В том случае, когда треугольные грани имеют одни и те же углы с основанием, возможно сделать вывод о том, что их рёбра одинаковы.

Свойства правильной пирамиды

У такой фигуры можно отметить особые свойства.

У правильной пирамиды все боковые треугольники одинаковы.

Каждая из них является равнобедренным треугольником.

Внутрь любой такого типа пирамиды можно вписать сферу. При этом она будет касаться основания и всех граней, имея с каждой из этих сторон по одной общей точке.

Снаружи возможна сфера, касающаяся всех вершин.

Нетрудно вычислить площадь поверхности такой фигуры. Для этого надо умножить длину периметра многоугольника, находящегося в её основании, на половину длины апофемы.

Особым случаем является ситуация, когда у вписанной и описанной сфер центры совпадают. В этом случае можно утверждать, что если сложить все плоские углы у боковых граней, то их сумма будет равна числу «Пи». При этом, для того чтобы узнать величину каждого из них, достаточно эту величину разделить на количество граней.