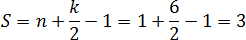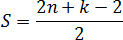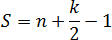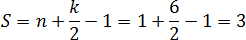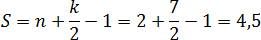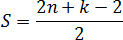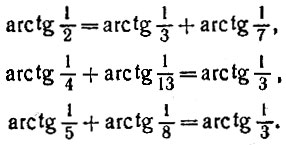Что такое вершины в узлах сетки
Метод узлов
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
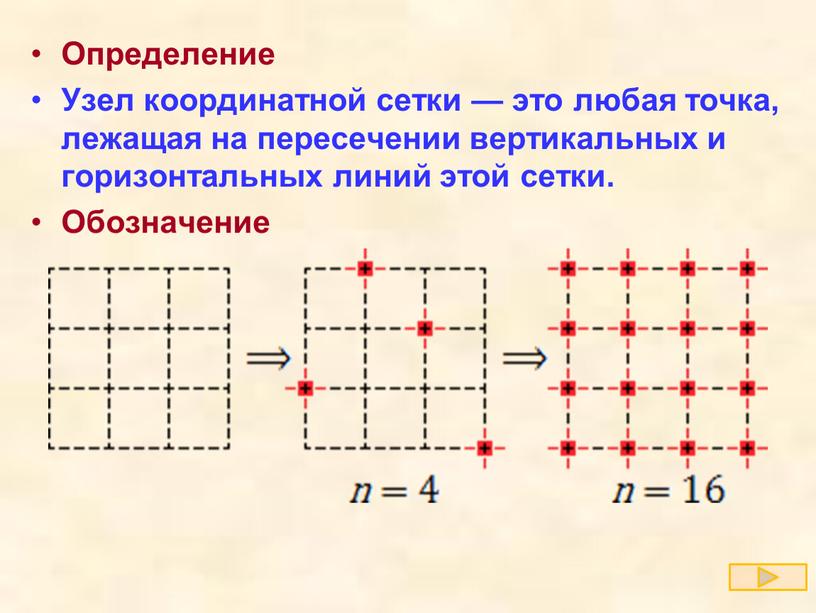
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
Обозначение
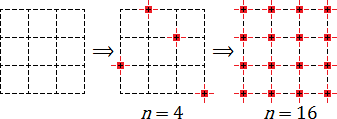
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
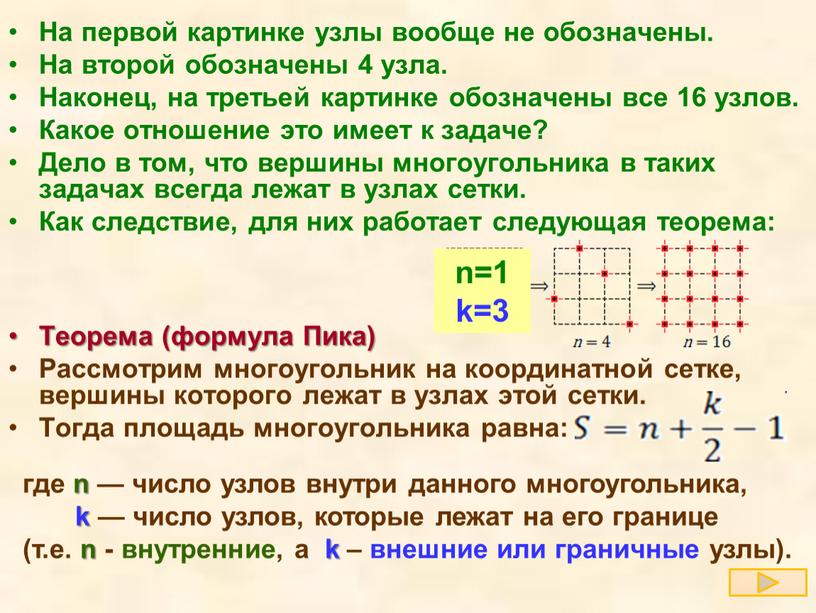
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема
Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
Задача:
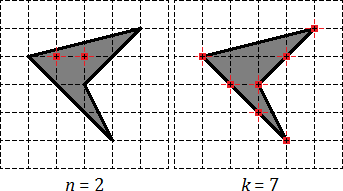
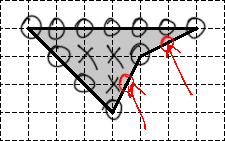
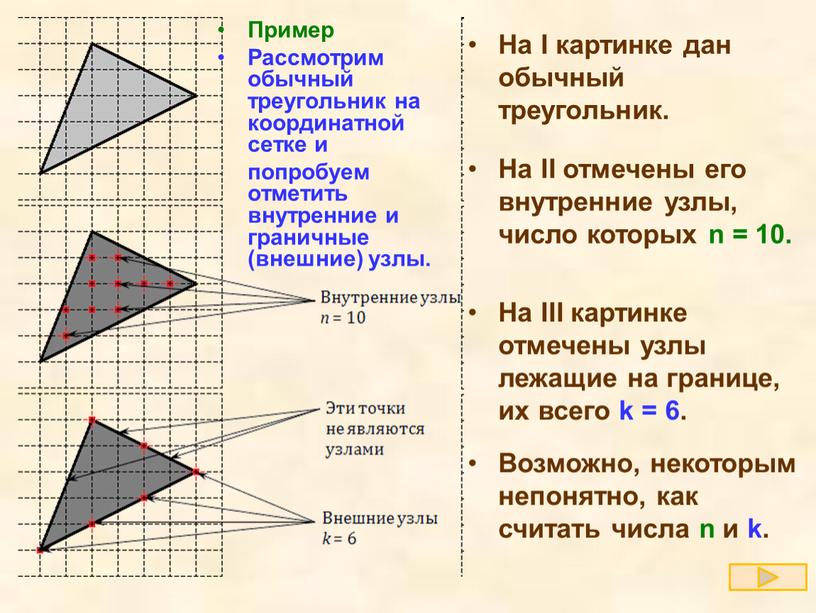
Рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
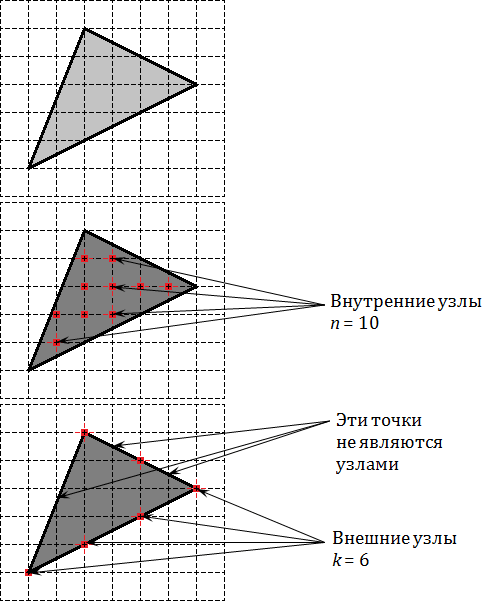
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
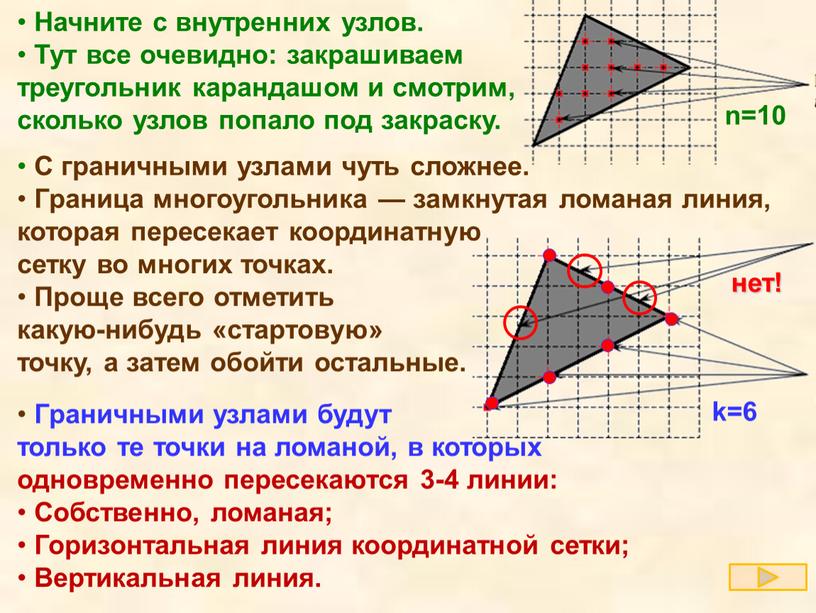
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача 2:
Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
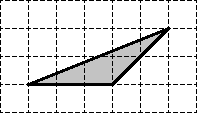
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
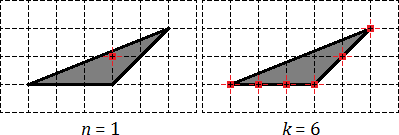
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача 3:
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
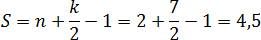
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
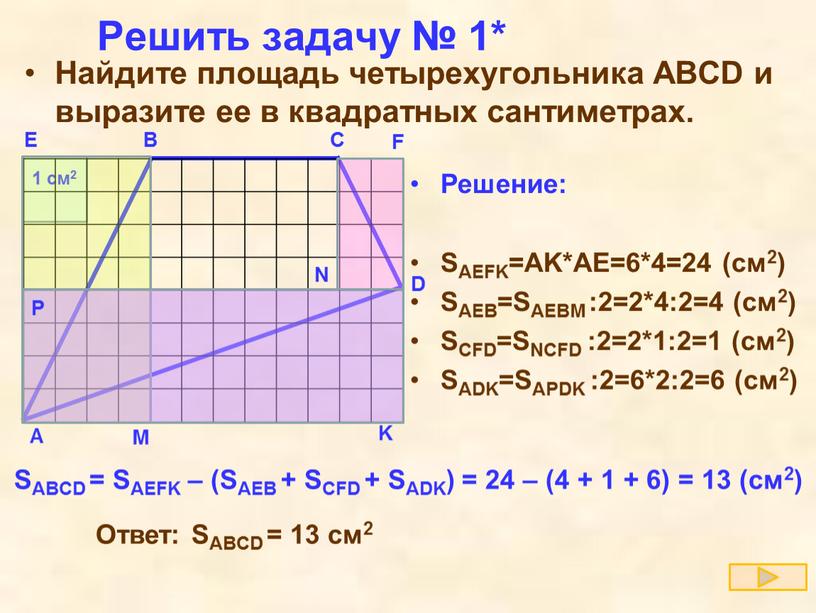
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»:
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Сегодня мы научились считать площади фигур в задаче B5 методом узлов. Повторим, что для начала введят два определения:
Давайте посмотрим, как эти узлы выглядят на конкретной фигуре в задаче B5
Задача. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
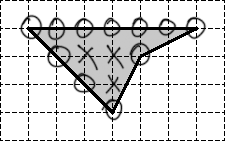
Крестиками обозначены внутренние узлы. Очевидно, их количество Кружками обозначены граничные узлы. Их общее количество равно
Обратите внимание: под узлами подразумеваются только те точки, которые лежат на пересечении горизонтальных и вертикальных линий нашей сетки. Другими словами, следующие две точки не являются узлами, хотя в них граница фигуры также пересекается с линиями сетки:
Переходим к решению задачи. Для того, чтобы решать задачи B5 ЕГЭ по математике методом узлов, вам потребуется запомнить следующую теорему:
Теорема. Пусть дана фигура с внутренними узлами и граничными узлами. Тогда площадь этой фигуры считается по формуле:
S = n + 0,5 k − 1
Вот так все просто! Главное — запомните, это число внутренних узлов, число граничных узлов.
В нашем случае мы уже подсчитали, что Подставляем полученные числа в формулу и получаем:
Мы получили ответ: площадь четырехугольника
Ответ: 7,5
Как видите, задача свелась практически к устному счету. Поэтому обязательно возьмите данный прием на вооружение, ведь велика вероятность того, что на настоящем ЕГЭ по математике вам попадется именно такая задача B5 — площадь фигур на координатной сетке.
Метод узлов в задаче B5
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.
Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
КДМ. Площадь многоугольника: разбиение фигуры на части и «метод узлов» по формуле Пика.
Площадь фигуры (многоугольника)
Площадь фигуры (многоугольника)
В задании требуется всегда одно и то же: найти площадь фигуры, которая задана точками на координатной плоскости или на координатной сетке
В задании требуется всегда одно и то же: найти площадь фигуры, которая задана точками на координатной плоскости или на координатной сетке.
В зависимости от фигуры, все задачи делятся на два типа:
Площадь многоугольника;
Площадь круга.
Независимо от типа, надо помнить важнейшее правило, вытекающее из свойств площади: если фигуру разрезать на несколько частей, то сумма площадей этих частей равна площади всей фигуры.
Рассмотрим площадь многоугольника.
Решить задачу № 1* Найдите площадь четырехугольника
Найдите площадь четырехугольника ABCD и выразите ее в квадратных сантиметрах.
Найдите площадь в см2
прямоугольника AEFK
Найдите площадь в см2
прямоугольных
треугольников AEB, CFD,
ADK
Найдите площадь четырехугольника ABCD
Решить задачу № 1* Найдите площадь четырехугольника
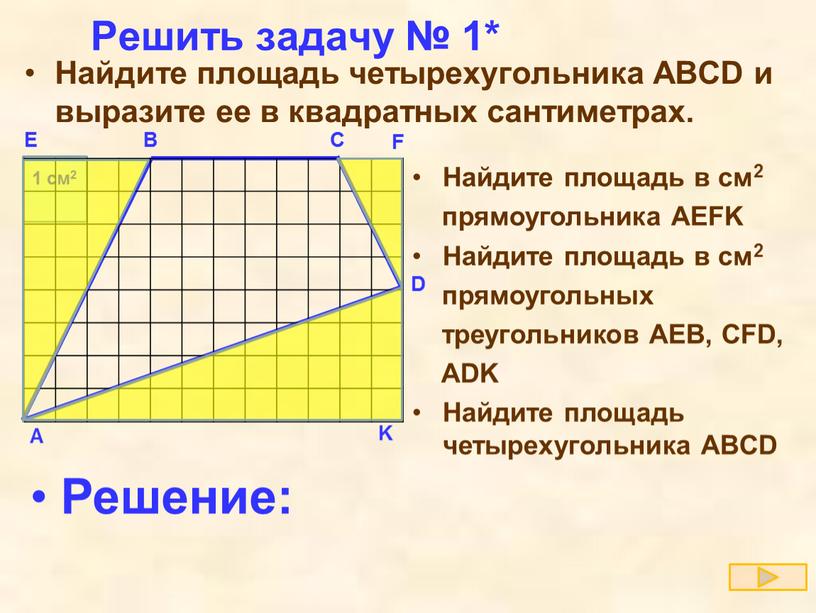
Найдите площадь четырехугольника ABCD и выразите ее в квадратных сантиметрах.
Найдите площадь
прямоугольника AEFK в см2
Найдите площадь прямоугольных треугольников AEB, CFD, ADK в см2
Найдите площадь четырехугольника ABCD
Решить задачу № 1* Найдите площадь четырехугольника
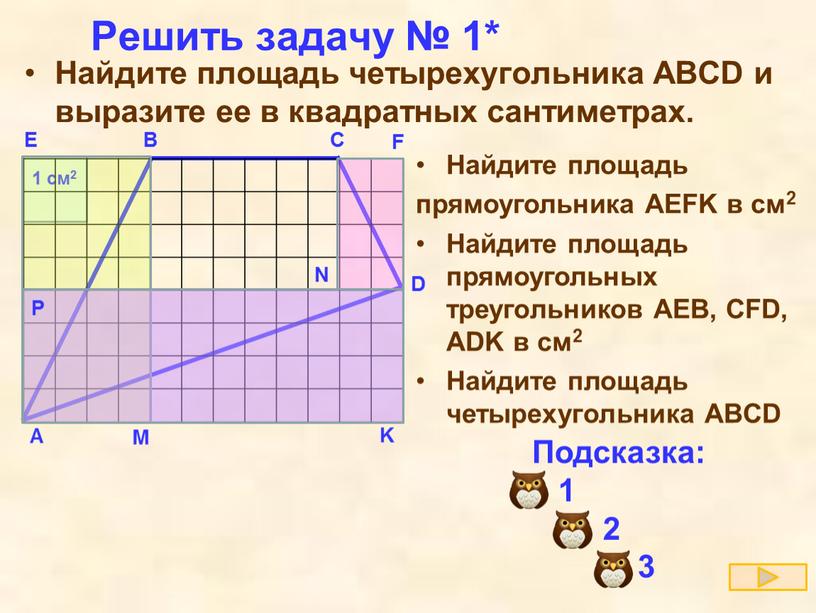
Найдите площадь четырехугольника ABCD и выразите ее в квадратных сантиметрах.
SAEFK=AK*AE=6*4=24 (см2)
SAEB=SAEBM :2=2*4:2=4 (см2)
SCFD=SNCFD :2=2*1:2=1 (см2)
SADK=SAPDK :2=6*2:2=6 (см2)
SABCD = SAEFK – (SAEB + SCFD + SADK) = 24 – (4 + 1 + 6) = 13 (см2)
Ответ: SABCD = 13 см2
Эту формулу редко кто изучает в школе…
Эту формулу редко кто изучает в школе…
О ней, вряд ли, вспомнят в колледже или даже в университете.
Но те, кто ее знают, всегда решат задачу правильно.
Никаких дополнительных построений и треугольников — все намного проще.
Запоминайте и пользуйтесь
замечательной формулой!
Метод узлов
А я знаю, как решить такую задачу намного проще и быстрее!
Есть отличная формула.
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок.
Это даже не формула, а настоящая теорема.
На первый взгляд, она может показаться сложной.
Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка.
Так что вперед!
Для начала введем новое определение:
Определение Узел координатной сетки — это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки
Определение
Узел координатной сетки — это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
Обозначение
На первой картинке узлы вообще не обозначены
На первой картинке узлы вообще не обозначены.
На второй обозначены 4 узла.
Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче?
Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки.
Как следствие, для них работает следующая теорема:
Теорема (формула Пика)
Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки.
Тогда площадь многоугольника равна:
Пример Рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные (внешние) узлы
Пример
Рассмотрим обычный треугольник на координатной сетке и
попробуем отметить внутренние и граничные (внешние) узлы.
На I картинке дан обычный треугольник.
На II отмечены его внутренние узлы, число которых n = 10.
На III картинке отмечены узлы лежащие на границе, их всего k = 6.
Возможно, некоторым непонятно, как считать числа n и k.
Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску
Начните с внутренних узлов.
Тут все очевидно: закрашиваем
треугольник карандашом и смотрим,
сколько узлов попало под закраску.
С граничными узлами чуть сложнее.
Граница многоугольника — замкнутая ломаная линия, которая пересекает координатную
сетку во многих точках.
Проще всего отметить
какую-нибудь «стартовую»
точку, а затем обойти остальные.
Граничными узлами будут
только те точки на ломаной, в которых
одновременно пересекаются 3-4 линии:
Собственно, ломаная;
Горизонтальная линия координатной сетки;
Вертикальная линия.
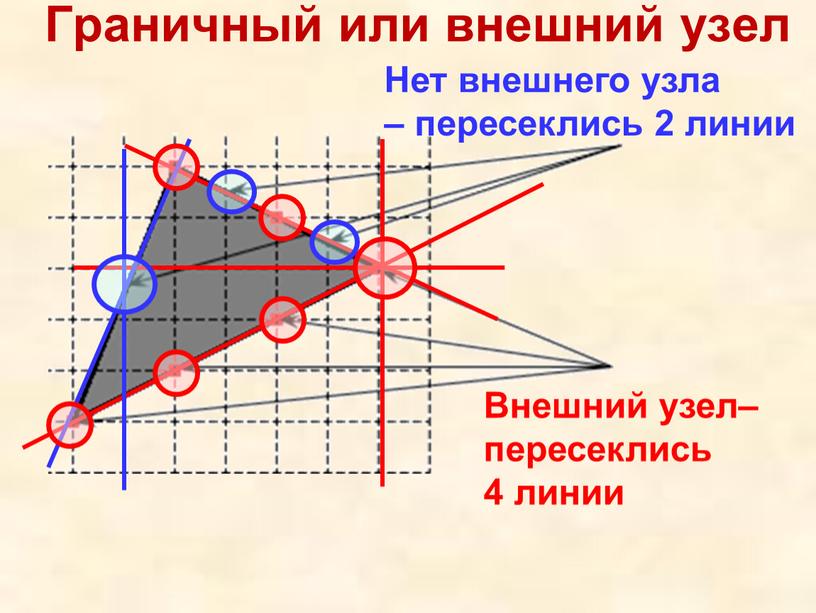
Граничный или внешний узел Нет внешнего узла – пересеклись 2 линии
Граничный или внешний узел
Нет внешнего узла
– пересеклись 2 линии
Внешний узел–
пересеклись
4 линии
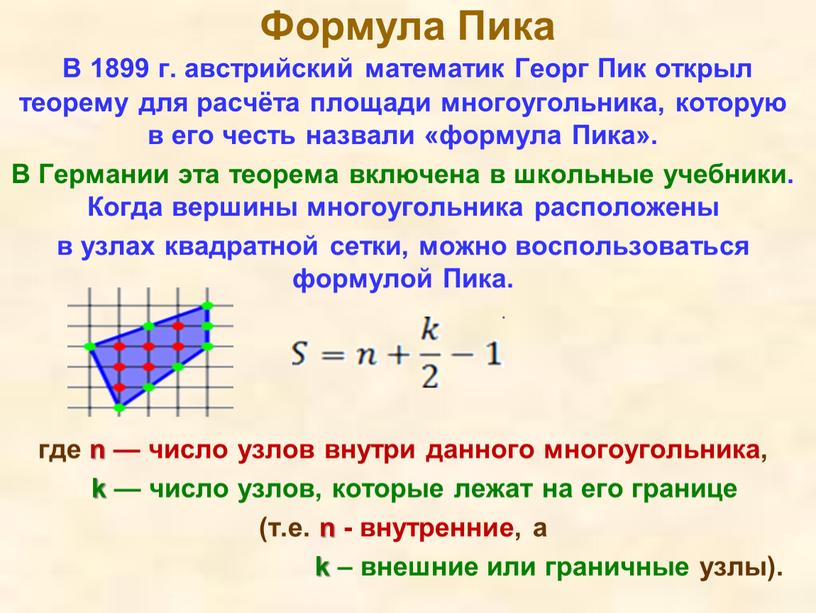
Формула Пика В 1899 г. австрийский математик
В 1899 г. австрийский математик Георг Пик открыл теорему для расчёта площади многоугольника, которую в его честь назвали «формула Пика».
В Германии эта теорема включена в школьные учебники. Когда вершины многоугольника расположены
в узлах квадратной сетки, можно воспользоваться формулой Пика.
Георг Алекса́ндр Пик (нем. Georg
ЛитЛайф
Жанры
Авторы
Книги
Серии
Форум
Сергеев Игорь Николаевич
Книга «Примени математику»
Оглавление
§ 16. Построения на клетчатой бумаге
Читать
Помогите нам сделать Литлайф лучше
§ 16. Построения на клетчатой бумаге
С бумагой в клетку каждый из вас имеет дело практически с первых дней изучения математики, а может быть, и раньше. Однако вы вряд ли представляете себе, насколько мощным инструментом для геометрических построений является наличие на бумаге квадратной сетки.
16.1. Середина отрезка На клетчатой бумаге нарисован отрезок, концы которого находятся в узлах сетки. Вам нужно найти его середину. Укажите, при каких положениях отрезка это можно сделать, не проводя дополнительных линий, а используя лишь точки пересечения отрезка с линиями сетки?
Как с помощью линейки найти середину отрезка при других его положениях?
16.2. Симметрия относительно точки Как проще всего найти точку, симметричную данному узлу сетки относительно другого данного узла сетки? Будет ли эта точка также узлом сетки?
16.3. На n частей Как разделить на заданное число n равных частей данный отрезок с концами в узлах сетки, пользуясь разве только линейкой?
16.4. Медианы треугольника В данном треугольнике с вершинами в узлах сетки проведите медианы, пользуясь одной лишь линейкой.
Обязательно ли точка пересечения медиан является узлом сетки?
16.5. Параллельный перенос Точки А, В и С находятся в узлах сетки. Не проводя никаких линий, параллельно перенесите точку С на вектор 
Будет ли полученная в результате точка узлом сетки?
16.6. Середина третьей стороны Докажите, что если какая-то вершина треугольника и середины двух прилежащих к ней сторон находятся в узлах сетки, то и середина третьей стороны также совпадает с одним из узлов сетки.
16.7. Параллельные прямые Через заданный узел сетки с помощью одной линейки проведите прямую, параллельную данной прямой, проходящей через два данных узла сетки. Отразите проведенную прямую симметрично относительно той же данной прямой.
16.8. Поворот на 90° Не проводя никаких линий, найдите точку, которая получится, если повернуть данный узел сетки вокруг другого данного узла сетки на угол 90°.
16.9. Вершины квадрата Докажите, что если две заданные соседние вершины квадрата находятся в узлах сетки, то и остальные две его вершины также должны находиться в узлах сетки.
Найдите эти вершины, не проводя никаких линий.
16.10. Перпендикуляр к прямой С помощью одной линейки через заданный узел сетки проведите прямую, перпендикулярную данному отрезку с концами в узлах сетки.
16.11. Симметрия относительно прямой Пользуясь одной лишь линейкой, отразите симметрично заданный узел сетки относительно данной прямой, проходящей через два данных узла сетки. Будет ли полученная в результате точка узлом сетки?
16.12. Рациональный тангенс Докажите, что проходящая через некоторый узел сетки прямая содержит еще хотя бы один узел тогда и только тогда, когда она образует с какой-нибудь линией сетки угол, тангенс которого является рациональным числом.
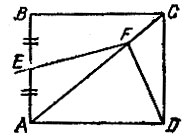
16.13. Без транспортира Найдите величину угла ABC, изображенного на рис. 63. Пользуясь полученным значением, сообразите в уме, чему равна сумма
16.15. Геометрия помогает тригонометрии Расположив на клетчатой бумаге угол DFE, описанный в задаче 16.14 и изображенный на рис. 64, подберите на луче FE несколько узлов сетки так, чтобы продемонстрировать равенства
16.16. Тангенсы углов треугольника Докажите, что если вершины треугольника лежат в узлах сетки, то тангенс любого непрямого угла этого треугольника является рациональным числом.
16.17. Другие повороты Прямая проходит через два заданных узла сетки. Предложите способ, как повернуть указанную прямую вокруг одного из этих узлов на угол, тангенс которого равен данному рациональному числу.
16.18. Правильный треугольник Докажите, что все вершины равностороннего треугольника не могут одновременно лежать в узлах сетки.
16.19. Правильный шестиугольник Могут ли все вершины правильного шестиугольника одновременно лежать в узлах сетки?
16.20. Одной окружностью Вы хотите разметить циркулем на клетчатой бумаге вершины правильного шестиугольника. Пользуясь циркулем, вы, конечно, всегда сможете это сделать на любой бумаге (см. задачу 15.5). Нельзя ли, однако, воспользоваться имеющейся сеткой с тем, чтобы после проведения специально подобранной вами окружности линии сетки сами указали вам на окружности вершины правильного шестиугольника?
16.21. Квадрат по трем линиям сетки На клетчатой бумаге требуется разметить вершины квадрата таким образом, чтобы три из них лежали соответственно на трех заданных параллельных линиях сетки. Как это сделать, не проводя никаких дополнительных линий?
Можно ли, кроме того, обеспечить попадание также и четвертой вершины квадрата на какую-нибудь из трех указанных линий?
16.22. Правильный многоугольник При каких значениях n все вершины правильного n-угольника могут одновременно лежать в узлах сетки?
16.23. С горизонтальной гипотенузой Если вам приходилось рисовать на клетчатой бумаге прямоугольные треугольники, то, наверняка, порядком наскучило располагать их катеты по линиям сетки. Можно ли построить такой прямоугольный треугольник со всеми вершинами в узлах сетки, чтобы на линии сетки оказалась его гипотенуза?
Равнобедренный прямоугольный треугольник так расположить довольно несложно. Укажите способ построения всех таких треугольников.
16.24. Окружность от руки Для проведения без циркуля какой-нибудь окружности на клетчатой бумаге, можно воспользоваться тем, что окружность с центром в узле сетки и радиусом 5 проходит через 12 узлов, изображенных на рис. 65. Докажите этот факт.
Существует ли окружность с центром в узле сетки и целым радиусом, меньшим 5, также содержащая более 4 узлов?
16.25. Окружность с 20 узлами Какого наименьшего целого радиуса должна быть окружность с центром в узле сетки, содержащая более 12 узлов? Нарисуйте хотя бы четверть этой окружности.