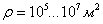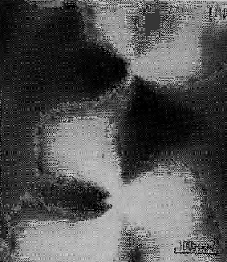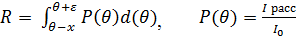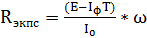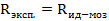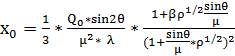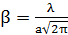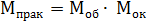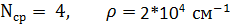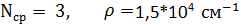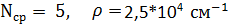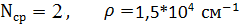Что такое винтовая дислокация

Дислокации – основы материаловедения

Дислокации — линейные дефекты кристаллической решетки типа обрыва или сдвига атомных плоскостей, нарушающие правильность их чередования. Энергия образования дислокаций существенно выше энергии образования точечных дефектов, поэтому они не могут существовать в измеримых концентрациях как термодинамически устойчивые дефекты. Они легко образуются при выращивании монокристаллов или эпитаксиальных пленок, сопровождающемся термическими, механическими и концентрационными напряжениями, приводящими к пластической деформации кристалла. Часть дислокаций может сохраняться в кристалле даже после самого тщательного отжига. Более подробно вопрос о причинах возникновения дислокаций будет рассмотрен при обсуждении методов выращивания монокристаллов и эпитаксиальных пленок (см. гл. 6

Рис. 3.4. а — Схема образования краевой дислокации. б — Расположение атомов вокруг краевой дислокации в простой кубической решетке.

и гл. 9), так как он имеет огромное значение для технологии полупроводников.

Поскольку дислокации при небольших концентрациях распределены по объему кристалла неравномерно, то нарушения свойств кристалла, обусловленные их присутствием, локализованы в небольших объемах, окружающих дислокации. Следовательно, кинетика процессов, протекающих вблизи этих дефектов, будет иной, чем в объеме кристалла, где дислокации отсутствуют.

Различают простые и смешанные дислокации. К простым дислокациям относят краевые и винтовые.

Рассмотрим кристалл, в котором в результате приложения внешних сил одна часть начинает смещаться относительно другой по некоторой плоскости (плоскости скольжения) вдоль некоторого выбранного направления (направления сдвига), то есть кристалл подвергается пластической деформации сдвига путем скольжения (рис. 3.4,а). Перемещения атомов по плоскости скольжения не являются равномерными, так как сдвиг на единицу скольжения происходит только в одной части кристалла, а в остальной части сдвиг полностью отсутствует. Перпендикулярную направлению сдвига линию AD, расположенную внутри кристалла и являющуюся границей между этими двумя частями кристалла, называют линией краевой дислокации и обозначают ⊥. Расположение атомов внутри деформированного скольжением кристалла в плоскости, перпендикулярной линии AD, имеет вид, изображенный на рис. 3.4,б. Атом, расположенный непосредственно над знаком дислокации ⊥, имеет окружение, отличающееся от окружения атомов в бездефектной части кристалла. Все происходит так, как если бы в объеме кристалла появилась

Рис. 3.5. Схема образования винтовой дислокации.

одна «лишняя» атомная плоскость, край которой обрывается внутри кристалла. Краевая дислокация, таким образом, представляет собой дефект, при котором одна из атомных плоскостей обрывается внутри кристалла по линии краевой дислокации AD, перпендикулярной направлению сдвига. Краевые дислокации образуются вдоль плоскостей скольжения. Условно подразделяют краевые дислокации на положительные и отрицательные. Положительная дислокация соответствует случаю, когда «лишняя» атомная плоскость находится сверху над знаком ⊥ (рис. 3.4,б) и в

верхней половине кристалла действуют сжимающие напряжения, в ниж

ней — растягивающие; а отрицательная — случаю, когда «лишняя» атомная плоскость находится снизу под знаком ⊥, то есть верхняя половина

кристалла растянута, а нижняя сжата.

Сдвиг одной части кристалла относительно другой, возникающий под влиянием внешних воздействий, может деформировать кристалл таким образом, что его можно представить состоящим из атомных плоскостей, закрученных в виде винтовой лестницы, ось которой и образует линию винтовой дислокации AD (рис. 3.5 и рис. 3.6). Винтовая дислокация

обозначается ⊗. Линия винтовой дислокации характеризуется тем, что

она параллельна направлению сдвига. При каждом обходе вокруг нее

мы поднимаемся или опускаемся на одно межплоскостное расстояние (рис. 3.6). Выход винтовой дислокации на поверхность кристалла заканчивается незарастающей ступенькой. В отличие от краевой дислокации, винтовая дислокация не имеет «лишних» плоскостей и может образовываться при сдвиге по любой атомной плоскости, проходящей через линию дислокации AD, то есть она не определяет однозначно плоскость скольжения. Различают правые и левые винтовые дислокации, причем направление вращения играет ту же роль, что и знак у краевых дислокаций.

Следует отметить, что в кристаллах полупроводников в чистом виде краевая и винтовая дислокации встречаются редко. Как правило, они по

Рис. 3.6. а — Винтовая дислокация. б — Расположение атомов на винтовой поверхности вдоль винтовой дислокации.

являются одновременно, приводя к образованию смешанных форм, при этом линия результирующей дислокации (граница между сдвинутой и не сдвинутой частями кристалла) не обязательно должна быть прямой, она может представлять собой произвольную кривую. Криволинейную дислокацию произвольной формы, которую можно представить как состоящую из различных комбинаций «чистых» краевой и винтовой дислокаций, называют смешанной. На рис. 3.7 показана смешанная дислокация в простой кубической решетке.

Основной характеристикой дислокации является вектор Бюргерса (вектор сдвига) b. Вектор Бюргерса — это мера искажений решетки, обусловленных присутствием дислокации. Для его определения строят замкнутый контур в кристалле с дефектом и контур, проходящий через те же атомы, в кристалле без дефекта. Проведем в решетке, содержащей краевую дислокацию, замкнутый контур A-B-C-D-A вокруг этой дислокации, начав его из произвольно взятого узла A и откладывая против часовой стрелки определенное число межатомных расстояний (рис. 3.8). Если построить тот же контур в решетке без дислокации, откладывая такое же число межатомных расстояний, то контур окажется незамкнутым. Вектор b, который необходимо добавить, чтобы замкнуть контур, и есть вектор Бюргерса. Величина разрыва контура характеризует сумму всех упругих смещений решетки, накопившихся в области вокруг дислокации. Для примера, изображенного на рис. 3.8 (простая кубическая решетка), вектор Бюргерса по абсолютной величине равен расстоянию между соседними атомами и ориентирован перпендикулярно линии дислокации.

Аналогичное построение для винтовой дислокации в простой кубиче

Рис. 3.7. a — Сдвиг, создавший смешанную дислокацию. б — Смешанная дислокация в простой кубической решетке. Краевая плоскость скольжения совпадает с плоскостью чертежа; черные кружки — атомы под плоскостью скольжения, белые — атомы над ней; заштрихованный участок — ступенька, образовавшаяся в результате сдвига.

Рис. 3.8. Контур и вектор Бюргерса краевой дислокации.

ской решетке показывает, что и в этом случае b равен расстоянию между соседними атомами (это шаг винта в направлении линии дислокации), но направлен вдоль линии дислокации.

Вектор Бюргерса — наиболее инвариантная характеристика дислокации. Он остается постоянным вдоль всей линии любой дислокации и сохраняется при ее движении [27].

Теперь можно дать определение простых дислокаций через вектор Бюргерса. Краевой дислокацией называют дислокацию, вектор Бюргерса b которой перпендикулярен линии краевой дислокации. Винтовой дислокацией называют дислокацию, вектор Бюргерса b которой параллелен линии винтовой дислокации. В общем случае смешанной дислокации вектор Бюргерса может иметь иные направления относительно линии дислокации.

Дислокации окружены полями упругих напряжений. Область над линией краевой дислокации, содержащая лишнюю полуплоскость, испытывает напряжения сжатия, область под линией дислокации — напряжения растяжения. Вокруг винтовых дислокаций существует поле сдвиговых (касательных) напряжений. Величина напряжений убывает обратно пропорционально расстоянию от линии дислокации [27].

Источник: И. А. Случинская, Основы материаловедения и технологии полупроводников, Москва — 2002

Источник

винтовая дислокация

Тематики

Смотреть что такое «винтовая дислокация» в других словарях:

винтовая дислокация — sraigtinė dislokacija statusas T sritis chemija apibrėžtis Sraigto pavidalo kristalo defektas, atsirandantis dėl įtempių lygiagrečiai pasislinkus gardelės mazgams. atitikmenys: angl. Burgers dislocation; screw dislocation rus. винтовая… … Chemijos terminų aiškinamasis žodynas

винтовая дислокация — sraigtinė dislokacija statusas T sritis fizika atitikmenys: angl. Burgers dislocation; screw dislocation vok. Burgers Versetzung, f; Querversetzung, f; Schraubenversetzung, f rus. винтовая дислокация, f; дислокация Бюргерса, f pranc. dislocation… … Fizikos terminų žodynas

дислокация — Термин дислокация Термин на английском dislocation Синонимы Аббревиатуры Связанные термины Определение линейный дефект кристаллической решетки, искажающий правильное расположение атомных (кристаллографических) плоскостей. Описание Дислокации… … Энциклопедический словарь нанотехнологий

Дислокация — Dislocation Дислокация. Линейный дефект в кристаллической атомной решетке. Два основных типа: (1) Краевая дислокация соответствует ряду несовпадающих атомов вдоль края дополнительной неполной плоскости атомов в пределах кристалла. (2) Винтовая… … Словарь металлургических терминов

дислокация Бюргерса — sraigtinė dislokacija statusas T sritis chemija apibrėžtis Sraigto pavidalo kristalo defektas, atsirandantis dėl įtempių lygiagrečiai pasislinkus gardelės mazgams. atitikmenys: angl. Burgers dislocation; screw dislocation rus. винтовая… … Chemijos terminų aiškinamasis žodynas

дислокация Бюргерса — sraigtinė dislokacija statusas T sritis fizika atitikmenys: angl. Burgers dislocation; screw dislocation vok. Burgers Versetzung, f; Querversetzung, f; Schraubenversetzung, f rus. винтовая дислокация, f; дислокация Бюргерса, f pranc. dislocation… … Fizikos terminų žodynas

ДИСЛОКАЦИЯ ВИНТОВАЯ — линейный дефект структуры, характеризующийся вектором сдвига, параллельным дислокации. См. Дислокация краевая. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

Дислокации — I Дислокации (геологические) (от позднелат. dislocatio смещение, перемещение), нарушения форм первичного залегания горных пород, вызванные тектоническими движениями земной коры, магматической деятельностью, метаморфизмом, экзогенными… … Большая советская энциклопедия

ДИСЛОКАЦИИ — (от позднелат. dislocatio смещение), дефекты кристалла, представляющие собой линии, вдоль и вблизи к рых нарушено характерное для кристалла правильное расположение ат. плоскостей. Механические свойства кристаллов прочность и пластичность в… … Физическая энциклопедия

Источник

Что такое винтовая дислокация

Строение реальных металлов. Дефекты кристаллического строения

Из жидкого расплава можно вырастить монокристалл. Их обычно используют в лабораториях для изучения свойств того или иного вещества.

Металлы и сплавы, полученные в обычных условиях, состоят из большого количества кристаллов, то есть, имеют поликристаллическое строение. Эти кристаллы называются зернами. Они имеют неправильную форму и различно ориентированы в пространстве. Каждое зерно имеет свою ориентировку кристаллической решетки, отличную от ориентировки соседних зерен, вследствие чего свойства реальных металлов усредняются, и явления анизотропии не наблюдается

В кристаллической решетке реальных металлов имеются различные дефекты (несовершенства), которые нарушают связи между атомами и оказывают влияние на свойства металлов. Различают следующие структурные несовершенства:

точечные – малые во всех трех измерениях;

линейные – малые в двух измерениях и сколь угодно протяженные в третьем;

поверхностные – малые в одном измерении.

Одним из распространенных несовершенств кристаллического строения является наличие точечных дефектов: вакансий, дислоцированных атомов и примесей. (рис. 2.1.)

Рис.2.1. Точечные дефекты

Вакансия – отсутствие атомов в узлах кристаллической решетки, «дырки», которые образовались в результате различных причин. Образуется при переходе атомов с поверхности в окружающую среду или из узлов решетки на поверхность (границы зерен, пустоты, трещины и т. д. ), в результате пластической деформации, при бомбардировке тела атомами или частицами высоких энергий (облучение в циклотроне или нейтронной облучение в ядерном реакторе). Концентрация вакансий в значительной степени определяется температурой тела. Перемещаясь по кристаллу, одиночные вакансии могут встречаться. И объединяться в дивакансии. Скопление многих вакансий может привести к образованию пор и пустот.

Дислоцированный атом – это атом, вышедший из узла решетки и занявший место в междоузлие. Концентрация дислоцированных атомов значительно меньше, чем вакансий, так как для их образования требуются существенные затраты энергии. При этом на месте переместившегося атома образуется вакансия.

Примесные атомы всегда присутствуют в металле, так как практически невозможно выплавить химически чистый металл. Они могут иметь размеры больше или меньше размеров основных атомов и располагаются в узлах решетки или междоузлиях.

Точечные дефекты вызывают незначительные искажения решетки, что может привести к изменению свойств тела (электропроводность, магнитные свойства), их наличие способствует процессам диффузии и протеканию фазовых превращений в твердом состоянии. При перемещении по материалу дефекты могут взаимодействовать.

Основными линейными дефектами являются дислокации. Априорное представление о дислокациях впервые использовано в 1934 году Орованом и Тейлером при исследовании пластической деформации кристаллических материалов, для объяснения большой разницы между практической и теоретической прочностью металла.

Дислокация – это дефекты кристаллического строения, представляющие собой линии, вдоль и вблизи которых нарушено характерное для кристалла правильное расположение атомных плоскостей.

Простейшие виды дислокаций – краевые и винтовые.

Краевая дислокация представляет собой линию, вдоль которой обрывается внутри кристалла край “лишней“ полуплоскости (рис. 2.2)

Рис. 2.2. Краевая дислокация (а) и механизм ее образования (б)

Неполная плоскость называется экстраплоскостью.

Большинство дислокаций образуются путем сдвигового механизма. Ее образование можно описать при помощи следующей операции. Надрезать кристалл по плоскости АВСD, сдвинуть нижнюю часть относительно верхней на один период решетки в направлении, перпендикулярном АВ, а затем вновь сблизить атомы на краях разреза внизу.

Наибольшие искажения в расположении атомов в кристалле имеют место вблизи нижнего края экстраплоскости. Вправо и влево от края экстраплоскости эти искажения малы (несколько периодов решетки), а вдоль края экстраплоскости искажения простираются через весь кристалл и могут быть очень велики (тысячи периодов решетки) (рис. 2.3).

Если экстраплоскость находится в верхней части кристалла, то краевая дислокация – положительная (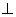), если в нижней, то – отрицательная (). Дислокации одного знака отталкиваются, а противоположные притягиваются.

Рис. 2.3. Искажения в кристаллической решетке при наличии краевой дислокации

Другой тип дислокаций был описан Бюргерсом, и получил название винтовая дислокация

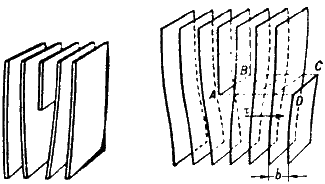
Винтовая дислокация получена при помощи частичного сдвига по плоскости Q вокруг линии EF (рис. 2.4) На поверхности кристалла образуется ступенька, проходящая от точки Е до края кристалла. Такой частичный сдвиг нарушает параллельность атомных слоев, кристалл превращается в одну атомную плоскость, закрученную по винту в виде полого геликоида вокруг линии EF, которая представляет границу, отделяющую часть плоскости скольжения, где сдвиг уже произошел, от части, где сдвиг не начинался. Вдоль линии EF наблюдается макроскопический характер области несовершенства, в других направлениях ее размеры составляют несколько периодов.

Если переход от верхних горизонтов к нижним осуществляется поворотом по часовой стрелке, то дислокация правая, а если поворотом против часовой стрелки – левая.

Рис. 2.4. Механизм образования винтовой дислокации

Винтовая дислокация не связана с какой-либо плоскостью скольжения, она может перемещаться по любой плоскости, проходящей через линию дислокации. Вакансии и дислоцированные атомы к винтовой дислокации не стекают.

В процессе кристаллизации атомы вещества, выпадающие из пара или раствора, легко присоединяются к ступеньке, что приводит к спиральному механизму роста кристалла.

Линии дислокаций не могут обрываться внутри кристалла, они должны либо быть замкнутыми, образуя петлю, либо разветвляться на несколько дислокаций, либо выходить на поверхность кристалла.

Дислокационная структура материала характеризуется плотностью дислокаций.

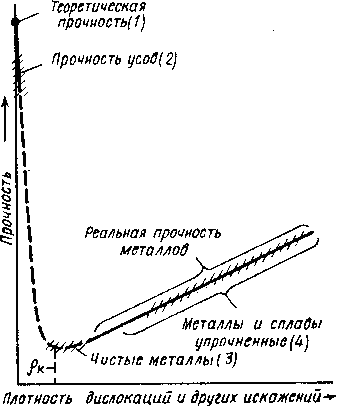
Плотность дислокации в значительной мере определяет пластичность и прочность материала (рис. 2.5)

Рис. 2.5. Влияние плотности дислокаций на прочность

Минимальная прочность определяется критической плотностью дислокаций

Дислокации влияют не только на прочность и пластичность, но и на другие свойства кристаллов. С увеличением плотности дислокаций возрастает внутреннее, изменяются оптические свойства, повышается электросопротивление металла. Дислокации увеличивают среднюю скорость диффузии в кристалле, ускоряют старение и другие процессы, уменьшают химическую стойкость, поэтому в результате обработки поверхности кристалла специальными веществами в местах выхода дислокаций образуются ямки.

Дислокации образуются при образовании кристаллов из расплава или газообразной фазы, при срастании блоков с малыми углами разориентировки. При перемещении вакансий внутри кристалла, они концентрируются, образуя полости в виде дисков. Если такие диски велики, то энергетически выгодно “захлопывание” их с образованием по краю диска краевой дислокации. Образуются дислокации при деформации, в процессе кристаллизации, при термической обработке.

Поверхностные дефекты – границы зерен, фрагментов и блоков (рис. 2.6).

Рис. 2.6. Разориентация зерен и блоков в металле

Размеры зерен составляют до 1000 мкм. Углы разориентации составляют до нескольких десятков градусов ().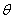

Граница между зернами представляет собой тонкую в 5 – 10 атомных диаметров поверхностную зону с максимальным нарушением порядка в расположении атомов.

Строение переходного слоя способствует скоплению в нем дислокаций. На границах зерен повышена концентрация примесей, которые понижают поверхностную энергию. Однако и внутри зерна никогда не наблюдается идеального строения кристаллической решетки. Имеются участки, разориентированные один относительно другого на несколько градусов (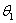). Эти участки называются фрагментами. Процесс деления зерен на фрагменты называется фрагментацией или полигонизацией.

В свою очередь каждый фрагмент состоит из блоков, размерами менее 10 мкм, разориентированных на угол менее одного градуса (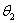). Такую структуру называют блочной или мозаичной.

Источник

Что такое винтовая дислокация

Из жидкого расплава можно вырастить монокристалл. Их обычно используют в лабораториях для изучения свойств того или иного вещества. Металлы и сплавы, полученные в обычных условиях, состоят из большого количества кристаллов, то есть, имеют поликристаллическое строение. Эти кристаллы называются зернами. Они имеют неправильную форму и различно ориентированы в пространстве.

Каждое зерно имеет свою ориентировку кристаллической решетки, отличную от ориентировки соседних зерен, вследствие чего свойства реальных металлов усредняются, и явления анизотропии не наблюдается.

В кристаллической решетке реальных металлов имеются различные дефекты (несовершенства), которые нарушают связи между атомами и оказывают влияние на свойства металлов.

Различают следующие структурные несовершенства:

Точеные дефекты

Одним из распространенных несовершенств кристаллического строения является наличие точечных дефектов: вакансий, дислоцированных атомов и примесей. (рис.1).

Вакансия – отсутствие атомов в узлах кристаллической решетки, «дырки», которые образовались в результате различных причин. Образуется при переходе атомов с поверхности в окружающую среду или из узлов решетки на поверхность (границы зерен, пустоты, трещины и т. д. ), в результате пластической деформации, при бомбардировке тела атомами или частицами высоких энергий (облучение в циклотроне или нейтронной облучение в ядерном реакторе). Концентрация вакансий в значительной степени определяется температурой тела. Перемещаясь по кристаллу, одиночные вакансии могут встречаться. И объединяться в дивакансии. Скопление многих вакансий может привести к образованию пор и пустот.

Дислоцированный атом – это атом, вышедший из узла решетки и занявший место в междоузлие. Концентрация дислоцированных атомов значительно меньше, чем вакансий, так как для их образования требуются существенные затраты энергии. При этом на месте переместившегося атома образуется вакансия.

Примесные атомы всегда присутствуют в металле, так как практически невозможно выплавить химически чистый металл. Они могут иметь размеры больше или меньше размеров основных атомов и располагаются в узлах решетки или междоузлиях.

Точечные дефекты вызывают незначительные искажения решетки, что может привести к изменению свойств тела (электропроводность, магнитные свойства), их наличие способствует процессам диффузии и протеканию фазовых превращений в твердом состоянии. При перемещении по материалу дефекты могут взаимодействовать.

Линейные дефекты

Основными линейными дефектами являются дислокации. Априорное представление о дислокациях впервые использовано в 1934 году Орованом и Тейлером при исследовании пластической деформации кристаллических материалов, для объяснения большой разницы между практической и теоретической прочностью металла.

Дислокация – это дефекты кристаллического строения, представляющие собой линии, вдоль и вблизи которых нарушено характерное для кристалла правильное расположение атомных плоскостей.

Простейшие виды дислокаций – краевые и винтовые.

Краевая дислокация представляет собой линию, вдоль которой обрывается внутри кристалла край “лишней“ полуплоскости (рис. 2).

Большинство дислокаций образуются путем сдвигового механизма. Ее образование можно описать при помощи следующей операции. Надрезать кристалл по плоскости АВСD, сдвинуть нижнюю часть относительно верхней на один период решетки в направлении, перпендикулярном АВ, а затем вновь сблизить атомы на краях разреза внизу.

Наибольшие искажения в расположении атомов в кристалле имеют место вблизи нижнего края экстраплоскости. Вправо и влево от края экстраплоскости эти искажения малы (несколько периодов решетки), а вдоль края экстраплоскости искажения простираются через весь кристалл и могут быть очень велики (тысячи периодов решетки) (рис. 3).

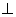
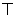
Если экстраплоскость находится в верхней части кристалла, то краевая дислокация – положительная (), если в нижней, то – отрицательная (). Дислокации одного знака отталкиваются, а противоположные притягиваются.

Винтовая дислокация получена при помощи частичного сдвига по плоскости Q вокруг линии EF (рис. 4). На поверхности кристалла образуется ступенька, проходящая от точки Е до края кристалла. Такой частичный сдвиг нарушает параллельность атомных слоев, кристалл превращается в одну атомную плоскость, закрученную по винту в виде полого геликоида вокруг линии EF, которая представляет границу, отделяющую часть плоскости скольжения, где сдвиг уже произошел, от части, где сдвиг не начинался. Вдоль линии EF наблюдается макроскопический характер области несовершенства, в других направлениях ее размеры составляют несколько периодов.

Винтовая дислокация не связана с какой-либо плоскостью скольжения, она может перемещаться по любой плоскости, проходящей через линию дислокации. Вакансии и дислоцированные атомы к винтовой дислокации не стекают.

В процессе кристаллизации атомы вещества, выпадающие из пара или раствора, легко присоединяются к ступеньке, что приводит к спиральному механизму роста кристалла.

Линии дислокаций не могут обрываться внутри кристалла, они должны либо быть замкнутыми, образуя петлю, либо разветвляться на несколько дислокаций, либо выходить на поверхность кристалла. Дислокационная структура материала характеризуется плотностью дислокаций.

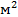
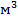
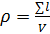
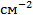
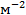
Плотность дислокаций в кристалле определяется как среднее число линий дислокаций, пересекающих внутри тела площадку площадью 1 , или как суммарная длина линий дислокаций в объеме 1 .

(, )

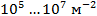
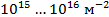
Плотность дислокаций изменяется в широких пределах и зависит от состояния материала. После тщательного отжига плотность дислокаций составляет , в кристаллах с сильно деформированной кристаллической решеткой плотность дислокаций достигает . Плотность дислокации в значительной мере определяет пластичность и прочность материала (рис. 5).

Дислокации влияют не только на прочность и пластичность, но и на другие свойства кристаллов. С увеличением плотности дислокаций возрастает внутреннее, изменяются оптические свойства, повышается электросопротивление металла. Дислокации увеличивают среднюю скорость диффузии в кристалле, ускоряют старение и другие процессы, уменьшают химическую стойкость, поэтому в результате обработки поверхности кристалла специальными веществами в местах выхода дислокаций образуются ямки.

Дислокации образуются при образовании кристаллов из расплава или газообразной фазы, при срастании блоков с малыми углами разориентировки. При перемещении вакансий внутри кристалла, они концентрируются, образуя полости в виде дисков. Если такие диски велики, то энергетически выгодно “захлопывание” их с образованием по краю диска краевой дислокации. Образуются дислокации при деформации, в процессе кристаллизации, при термической обработке.

Поверхностные дефекты – границы зерен, фрагментов и блоков (рис. 6).

Размеры зерен составляют до 1000 мкм. Углы разориентации составляют до нескольких десятков градусов ().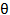

Граница между зернами представляет собой тонкую в 5 – 10 атомных диаметров поверхностную зону с максимальным нарушением порядка в расположении атомов.

Строение переходного слоя способствует скоплению в нем дислокаций. На границах зерен повышена концентрация примесей, которые понижают поверхностную энергию. Однако и внутри зерна никогда не наблюдается идеального строения кристаллической решетки. Имеются участки, разориентированные один относительно другого на несколько градусов (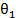). Эти участки называются фрагментами. Процесс деления зерен на фрагменты называется фрагментацией или полигонизацией.

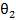
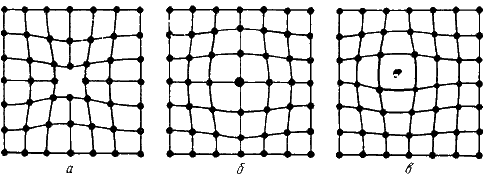
В свою очередь каждый фрагмент состоит из блоков, размерами менее 10 мкм, разориентированных на угол менее одного градуса (). Такую структуру называют блочной или мозаичной.

Большинство методов экспериментального наблюдения дислокаций основано на регистрации напряжений или искажений в решетке, обусловленных дислокацией.

Метод избирательного травления.

Избирательное травление – обработка поверхности кристалла специально подобранным химическим реактивом, в результате действия которого на поверхности образуются мелкие ямки (или бугорки), называемые фигурами травления. Огранка фигуры травления зависит от симметрии грани кристалла. Фигуры травления образуются в тех местах, где на поверхности кристалла выходит дислокация и, значит, структура кристалла нарушена. Расположение и число фигур травления характеризуют дислокационную структуру кристалла (рис.7). По числу ямок травления на 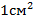площади определяют плотность дислокаций.

Соответствие каждой фигуры травления месту выхода дислокации может быть показана с помощью одного из следующих методов.

Послойное травление. Протравленную поверхность кристалла с образовавшимися на ней фигурами травления фотографируют и после этого сполировывают с нее тонкий слой так, чтобы при этом не нарушалась дислокационная структура поверхности. Механическая полировка здесь непригодна, потому что при механической шлифовке или полировке создаются новые дислокации; применять можно лишь химическую или ионную полировку. После полировки производят повторное травление той же поверхности тем же травителем и сравнивают полученную картинку с предыдущей. Так как дислокация – линейный дефект, протяженный в глубь кристалла, то новые фигуры травления должны оказаться практически на тех же местах, где они были раньше, если они действительно отвечают выходам дислокаций. Если же фигуры травления соответствуют не дислокациям, а поверхностным или каким-либо другим дефектам, то новое расположение фигур травления не повторяет старое.

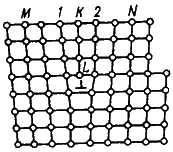
Метод сравнения парных поверхностей раскола по спайности. Если расколоть кристалл по плоскости спайности и протравить две парные поверхности раскола, то дислокации, пересекающие поверхность раскола, должны дать зеркально-симметричную картину соответствующих фигур травления, что и наблюдается в действительности (рис. 8). Метод сравнения парных граней очень удобен для регистрации изменения дислокационной структуры кристалла в результате каких-либо внешних воздействий. Например, раскалывая кристалл по спайности, подвергают затем одну из полученных половинок кристалла пластической деформации и сравнивают распределение дислокаций на деформированной и недеформированной половинах образца.

По фигурам травления можно наблюдать за движением дислокаций. Протравим поверхность кристалла и найдем на ней фигуры травления. Затем подвергнем кристалл действию внешнего напряжения. В результате дислокация сдвинется со своего места. Вторично протравим прежним травителем ту же грань кристалла. Так как на ее поверхности уже имелись ямки травления, они будут растворяться интенсивнее, чем окружающие их участки. Однако теперь в этом месте нет выхода дислокации, поэтому ямка травления будет увеличиваться не вглубь, а только вширь. На месте прежней фигуры травления образуется расширившаяся, но неглубокая фигура травления. В отличие от нее на том месте, где теперь выходит дислокация, образуется новая ямка травления, которую по виду легко отличить от старой: новая фигура травления мельче, но глубже тех, которые возникли на месте старых. Таким образом, при повторном травлении видны плоские большие фигуры в тех местах, где дислокация была, но теперь оттуда ушла, и мелкие остроконечные фигуры в тех местах, где дислокация теперь выходит на поверхность кристалла, т.е куда она перешла (рис. 9). Сравнение старых и новых фигур травления по их положениям на грани кристалла позволяет проследить путь, пройденный дислокацией, а одновременное измерение длительности процесса позволяет определить скорость перемещения дислокаций (рис. 9, 10). Так, на рис. 11 показано расширение дислокационной петли в кристалле KBr, которое произошло под действием мгновенной нагрузки 7 Мпа в течении 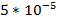c.

Рис. 10 Фигуры травления на грани (100) кристалла LIF, иллюстрирующие движение дислокаций. Увеличение 300х

Рис. 11 Движение дислакацоинной петли в кристалле KBr; а- фотография фигур травления, б-схема. Стрелками показано направление перемещения дислокаций.

По фигурам травления можно наглядно проследить за образованием и движением дислокаций в процессе пластической деформации. На рис.12 видна «звезда фигур травления» на грани (100) кристалла фтористого лития, образовавшаяся около того места, где на грань кристалла действовала сосредоточенная нагрузка. В центре звезды виден темный ромбик – отпечаток четырехугольной алмазной пирамиды, вдавившейся в кристалл и создавшей пластическую деформацию. В пластически деформационной области создалось множество дислокаций, движущихся по плоскостям скольжения.

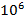
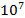
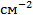
Определения плотности дислокаций по фигурам травления является основным промышленным методом контроля качества кристалла, но этот метод применим лишь для кристаллов с плотностью дислокаций, меньшей чем ( — ) . При большей плотности дислокаций уже не удается различать отдельные фигуры травления, они все сливаются друг с другом.

Еще более нагляден, но и более сложен по технике эксперимента метод декорирования, в котором дислокации делаются видимыми, потому что на них осаждаются чужеродные частицы (см. рис.13). Так, если кристалл кремня подвергнуть отжигу в парах золота, то частицы золота осаждаются вдоль дислокационных стенок, делая их видимыми. В отличие от метода травления метод декорирования позволяет наблюдать дислокационную структуру не только на поверхности, но и в глубине кристалла. На рис.13 видны два отрезка одной дислокационной петли и рождаемые ими новые дислокационные петли. Такая конфигурация называется источником Франка – Рида.

Недостатком метода декорирования является то, что дислокация, на которой выделялись частицы, уже не может двигаться. Поэтому метод декорирования непригоден для наблюдения за изменением дислокационной структуры, но в сочетании с травление он дает возможность сопоставить распределение дислокаций на поверхности с их распределением в глубине кристалла.

Собственные поля напряжений дислокации, складываясь, создают заметные концентрации напряжений внутри кристалла, которые можно наблюдать благодаря пъезооптическому эффекту (фотоупругости). Этот метод особенно удобен для исследования дислокаций в кубических кристаллах, которые в ненапряженном состоянии оптически изотропны. Поля напряжений дислокаций а них регистрируются по возникающему двойному лучепреломлению. На рис.14 показано распределение дислокаций в кристаллографической пластинке кремния, регистрируемое по методу травления, методу декорирования и по двойному лучепреломлению. Видно, что во всех случаях картины распределения дислокаций совпадают.

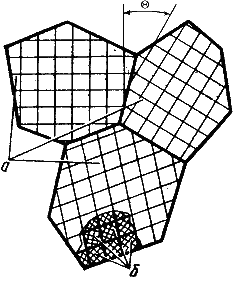
Рис. 14 Дислокационная структура пластинки кремяния, выявленная различными методами: а-напряжение вокруг дислокаций, видимые по двойному лучепреломлению в поляризованном свете; б – ямки травления на поверхности образца; в-декорирование дислокации; г-схема расположения дислокаций в образце. Стрелки указывают напрвление краевых компонент

По двойному лучепреломлению в поляризованном свете можно выявить характерную картину распределения напряжений вокруг отдельной дислокации, описываемого формулами (5.6)-(5.8) (рис. 15-16). Ряды дислокаций, скопившихся в плоскостях скольжения или в доменных стенках, видны в поляризационном свете как полосы двойного лучепреломления (рис.17).

Рис. 15 Расчетные поля напряжений вокруг отдельных краевых дислокаций в кристалле граната

Рис. 16 Поля напряжений вокруг отдельных краевых дислокаций в кристалле граната, экспереминтально наблюдаемые в поляризованном свете

Рис. 17 Полосы двупреломления вдоль плоскостей скольжения <110>в изогнутом кристалле фтористого лиия. Увеличение 60х

Электронная микроскопия и рентгеновские методы

Это самые мощные из экспериментальных методов прямого наблюдения дислокаций. Метод наблюдения дислокаций с помощью электронного микроскопа, применяемый очень широко, основан на эффекте дислокационного контраста, возникающего из-за взаимодействия электронного пучка со смещенными атомами в поле напряжений вокруг дефекта решетки. Вследствие интерференции между проходящими и дифрагированными электронными лучами в электронном микроскопе удается увидеть изображение линий дислокаций, дефектов упаковки, дислокационных рядов и стенок.

Возможности этого метода ограничены шириной пучка, позволяющей исследовать лишь небольшой участок кристалла и, главное, тем, что можно исследовать материалы лишь в виде тонких пленок толщиной не больше 100-500 нм. Для получения такой пленки материал прокатывается до тонкой фольги или утоньшается другими методами: резкой, механической или химической полировкой. Однако при всех этих обработках в пленку вносятся новые дефекты, поэтому дислокационная структура пленкине соответствует структуре массивного образца, т.е по получаемой картине нельзя одназначно судить о структуре исходного кристалла. Лучшие результаты получаются при исследовании выращенных тонких эпитаксиальных пленок, однако и здесь возникают специфические трудности, связанные с тем, что в таких тонких пленках влияние поверхности на образование и движение дефектов значительно больше и качественно иное, чем в массивных образцах, которые можно считать по сравнению с дислокацией практически бесконечными. Тем не менее методом электронной микроскопии получены основные данные о дислокационной структуре многих веществ, движении дислокаций, дефектах упаковки и взаимодействии различных дефектов решетки друг с другом (рис. 18-21). С помощью электронного микроскопа удается разрешать отдельные плоскости решетки и непосредственно видеть отдельные дислокации (см. рис. 21).

Рис. 18 Сетки дислокаций в плоскости (0001) вкристалле цинка. Рис. 19 Ряды атомов и краевая дислокация в кристалле CuS.

Рис. 20 Сетка дислокаций в кристалле кремнистого железа. Рис. 21 Ряды атомов и дислокации в тонкой пленке палладия,напыленный на монокристалл золот

Рис. 22 Дислокация в кристалле кремния толщинной 0,5 мм.

Метод рентгеновской топографии

Он дает возможность исследовать толстые и достаточно большие образцы. В этом методе используется брэгговское рентгеновское отражение, а дифракционный контраст получается из-за того, что локальная деформация решетки, связанная с дефектом, изменяет условия отражения и рассеяния рентгеновских лучей. Интенсивность дифрагированного рентгеновского пучка вблизи дефекта уменьшается, вследствие чего дефект виден как темная линия на общем светлом фоне (рис. 22).

Эти и многие другие, прямые или косвенные, методы позволяют видеть дислокации на поверхности или в объеме образца, следить за их движением и взаимодействием.

Важнейшим дефектом кристаллов являются дислокации, приводящие к разориентировки соседних областей кристалла.

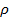
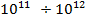
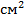
Одной из характеристик степени совершенства монокристаллов является плотность дислокаций , определяемая как число выходов дислокаций на единицу поверхности. Плотность дислокаций в кристаллах может изменяться от нуля (идеальный кристалл) до дислокаций на 1 . Последнее значение плотности дислокаций характерны для так называемого идеально-мозаичного кристалла.

Разработаны различные “прямые” методы определения плотности дислокаций в кристаллах: метод избирательного травления, методы рентгеновской топографии и т. д.

Наряду с ними развиваются рентгеновские методы определения плотности дислокаций 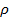по интегральным интенсивностям брэгговских отражений. Эти методы дают ряд преимуществ, главное из которых заключается в возможности определения значений плотности дислокаций в широком интервале значений без разрушения кристаллов.

Характеристикой отражательной способности кристалла является интегральная интенсивность. Интегральная интенсивность-величина, определяющая полную энергию, рассеянную в направлении главного максимума. Интегральную интенсивность можно определить по площади, ограничивающей кривую распределения интенсивности, получаемой при повороте кристалла около отражающего положения в интервале углов рассеяния 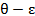, . 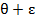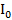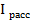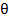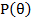В этом случае все блоки мозаики независимо от их ориентации пройдут через отражающее положение. Интегральная интенсивность задается выражением:

– интенсивность первичного пучка рентгеновский лучей,
– интенсивность рассеянного рентгеновского излучения при данном угле падения,
– коэффициент интегрального отражения.

Пределы интегрирования выбраны так, чтобы интервал, ограниченный ими, полностью захватывал только один интерференционный максимум.

Теоретическая формула для расчета интенсивности интегрального отражения принимает совершенно различный вид, в зависимости от того, считаем мы, что кристалл является совершенным или что он является идеально-мозаичным. т.е. состоит из мелких, почти параллельных блоков с настолько малыми размерами. Что эффектом поглощения и многократного отражения рентгеновских лучей внутри него можно пренебречь. Реальный кристалл находится между двумя предельными состояниями кристалла.

Методы измерения интегральной интенсивности

Известны четыре способа измерения интегральной интенсивности:

При конечных размерах кристалла углы обратной решетки нельзя считать геометрическими точками, узлы поэтом размыты. Это обстоятельство влияет на зависимость интегральной интенсивности от брэгговского угла. Пусть 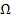– телесный угол. Под которым из центра сферы отражения видно сечение этой сферой узла обратной решетки L (рис.1.).

Для получения кривых распределения интенсивности в зависимости от угла рассеяния, которое называют кривыми качания, используется метод двухкристального спектрометра. В двухкристальном спектрометре рентгеновские лучи последовательно отражаются от двух плоских кристаллов, из которых первый имеет совершенное строение, а второй (исследуемый образец 2 – мозаичное. Данный метод позволяет применять две схемы установки кристаллов. По первой схеме (рис.2, а) пучок рентгеновских лучей падает на совершенный кристалл 1, установленный в отражающем положении под брэгговским углом 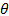. 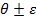Отражаемый от этого кристалла монохроматический пучок падает на исследуемый кристалл 2, установленный в отражающем положении, но его поверхность не параллельна поверхности кристалла 1. Такое положение называется антипараллельным и обычно обозначается символом (m, n), где m и n – порядки отражения кристалла монохроматора и исследуемого кристалла соответственно. Исследуемый кристалл поворачивают на небольшие углы в интервале до тех пор, пока кристалл не выйдет из отражающего положения. В антипараллельном положении дисперсии равна сумме угловых дисперсий каждого из кристаллов.

В работе интегральные интенсивности рассеяния монокристаллов предлагается измерить на рентгеновской установке ДРОН-3.0 в молибденовом излучении, монохроматизированном отражении от монокристалла Si (111), установленном в первичном пучке. Для уменьшения расходимости первичного пучка установлены стандартный коллиматор и система щелей шириной 0.25 мм и высотой 0.08 мм.

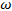
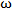
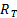
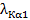
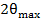
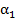
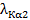
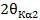
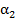
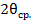
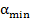
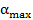
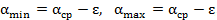
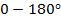
В данной работе используется метод — сканирования. Кристалл выводится в отражающее положение таким образом, чтобы при его покачивании вокруг оси гониометра с угловой скоростью весь отраженный пучок рентгеновский лучей полностью попадал в щель детектора. Юстировка образца производится следующим образом. Образец устанавливается в стандартном держателе, позволяющем осуществлять вращение в своей плоскости. Далее детектор выводится на расчетный угол соответствующий отражению от плоскости (HKL) пучка с диной волны . Оси вращения образца и счетчика расцепляются. Перед счетчиком устанавливается щель шириной 0.1-0.25 мм, и путем перемещения счетчика добиваются получения максимума интенсивности. Затем та же процедура юстировки повторяется при перемещении образца при фиксированном положении детектора, соответствующего . В результате определяем значение угла по шкале образца . Путем вращения кристалла в своей плоскости добиваемся максимума интенсивности. Правильность юстировки проверяется при изменении высоты щели пред счетчиком. При правильной юстировке кристалла уменьшение высоты щели на 50% не должно приводить к уменьшению интенсивности рассеяния. Далее оси вращения образца и счетчика жестко скрепляются, и выводится отражение от этой же плоскости, соответствующее длине волны . После уточнения углов , , счетчик устанавливается под углом . Щели перед счетчиком удаляется. Рассчитывается среднее значение угла установки образца. Образец сканируется в интервале углов — , . Значения интегральной интенсивности каждого отражения получаются в результате усреднения не менее 2-х измерений, полученных в результате сканирования “вперед-назад”. Кроме того для минимизаций погрешности, связанной с возможным отклонением отражающей плоскости от поверхности кристалла, образцы следует рентгенографировать в положениях . Фон измеряется на “хвостах” линии с обеих сторон от максимума за 100 сек. и усредняется. Интервал углов сканирования необходимо задавать таким образом. Чтобы фон на “хвостах” кривой качания с обеих сторон был примерно одинаков (отличие в значениях интенсивности рассеяния не должно выходить за рамки погрешности эксперимента) (рис.3).

Экспериментальные значения интегральной интенсивности рассеяния 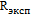определяется по формуле (2):

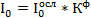
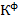
При нахождении интегральных интенсивностей важную роль играет измерение интенсивности первичного пучка. Измерение интенсивности первичного пучка необходимо производить несколько раз до и после сканирования образца. Интенсивность первичного пучка измеряется после ослабления пакетом фильтров&nbsp- , где коэффициент ослабления, в данной работе равен 28.7.

Точное значение интегральной интенсивности строго теоретически можно получить только для двух крайних типов кристалла-совершенного и идеально-мозаичного.

Мозаичным называют кристалл, состоящий из очень большого числа настолько малых блоков, чтобы поглощением в них можно было пренебречь. Причем эти блоки разориентированы друг относительно друга так, что отражение от них можно считать оптически независимыми. Это значит, что между ними не существует закономерного соотношения фаз. Поэтому для получения полной интенсивности отражения таким идеально-мозаичным кристаллом достаточно просто сложить интенсивности отражений каждым отельным блоком. Расчет интегральной интенсивности отражений в этом случае 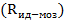ведется на основе кинематической теории.

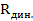
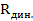
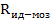
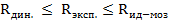
Эти два значения интегральной интенсивности и интегральной интенсивности реального кристалла находится в области значений и , причем для брэгговской геометрии справедливо соотношение, причем для брэгговской геометрии справедливо соотношение . Поэтому можно записать:

Несоответствие теоретических и экспериментальных интегральных интенсивностей объясняется экстинкционными эффектами. Различают первичную и вторичную экстинкции. Первичной экстинкцией называют уменьшение интенсивностей за счет динамического взаимодействия падающего и отраженного лучей в идеальном кристалле. Чтобы понять возникновение первичной экстинкции, рассмотрим модель совершенного кристалла, предложенную Дарвиным (рис.4). Пусть кристалл находится в отражающем положении. Тогда первичный пучок, проходя через кристалл, поглощается. Поглощение характеризуется линейным коэффициентом поглощения 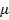. 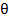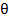Если кристалл находится в отражающем положении под брэгговским углом , то отраженные от атомных плоскостей лучи падают на лежащие выше атомные плоскости под углом и испытывают повторное отражение.

Уменьшение интегральной интенсивности за счет экранировки нижних блоков верхними в мозаичном кристалле называют вторичной экстинкцией. Пусть кристалл состоит из блоков, незначительно разориентированных друг относительно друга (рис.5). Тогда интенсивность первичного пучка, дошедшего до блока 2, ослабляется в ,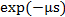
где 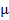-линейный коэффициент поглощения, s- путь первичного пучка в кристалле до блока 2. Если же на пути первичного пучка встретиться еще один блок 1, ориентированный аналогично блоку 2, то интенсивность первичного пучка будет уменьшена вследствие отражения блоком 1.

Теоретические формулы для интегральной интенсивности вычислены Дарвиным для “толстого” кристалла в форм плоскопараллельной пластины:

1) для идеального кристалла без учета поглощения-

2) для идеально-мозаичного кристалла-

Для дальнейших расчетов удобно ввести величину интегрального отражения единицей объема-

В работе экспериментальные значения интегральной интенсивности будем сравнивать с теоретическими значениями, рассчитанными по формуле (6) для толстого кристалла. Т.е.

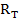
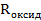
Таким образом, рассчитав , определить из эксперимента , по формуле (3) находим значение экстинкционнго параметра y.

Теоретическая формула зависимости экстинкционного параметра от плотности дислокаций для брэгговского случая “толстого” кристалла имеет вид:

— рассчитывается по формуле:

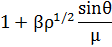
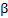
Если исследуемый монокристалл представляет собой соединение или твердый раствор, то массовые коэффициенты поглощения вычисляются из соотношения:

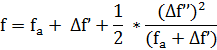
Таблица 2

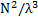(HKL)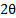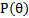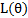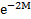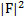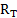

(HKL)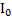

№

, и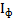мп/с

, имп/с

t, сек

Е, имп

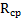
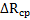
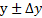
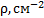0

10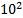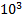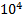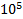

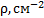
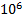
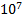
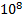
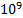
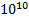
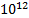
Контрольные вопросы

ЛАБОРАТОРНАЯ РАБОТА

Определение плотности дислокаций методом оптической микроскопии

Теоретическая часть

Большинство материалов относятся к кристаллическим веществам, в которых составляющие их частицы (атомы, ионы, молекулы) расположены в периодически повторяющейся последовательности.

Многообразие физических свойств большинства материалов определяются их структурой. Понятие структуры в применении к этим объектам включает в себя:

а) особенности строения, видимые либо визуально, либо при помощи оптических приборов, дающих небольшие ( до х30) увеличения.Такие характеристики определяются термином “макроструктура”;
б) межфазные границы, размеры и формы включений присутствующих фаз и их количественное соотношение: размеры и форсы зерен для однофазных систем. Этот комплекс понятий объединяется в термин “микроструктура”. Микроструктура выявляется при использовании оптических приборов, дающих увеличение (х30, х1500) и электронной микроскопии (до х50000);
в) атомно-молекулярное строение или субмикроструктура.
Субмикроструктура изучается с помощью электронных микроскопов и методами дифракции рентгеновских лучей или нейтронов.

Металлографические исследования позволяют получать сведение о микроструктуре объектов (шлифов). При помощи металлографического анализа можно решать достаточно корректно 3 задачи:

1. Определение среднего размера зерен однофазных материалов;
2. Нахождение средних размеров фазных включений или распределение фазных включений по размерам;
3. Определение относительного содержания фаз в двух- или в многофазных системах.
4. Под фазой понимают часть или совокупность гомогенных частей системы, отделенных от других частей системы поверхностью раздела и характеризующихся в отсутствии внешних воздействий одинаковыми свойствами и составом во всех своих точках.
Ход лучей в оптическом микроскопе показан на рис.6.

Максимальное (полезное) увеличение микроскопа зависит от разрешающей способности глаза и микроскопа и может быть определено, используя соотношение:

где – максимальная разрешающая способность человеческого глаза, равная 0,3 мм;
– максимально разрешающая способность оптического микроскопа.
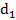
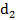
Увеличение сложного микроскопа определяется формулой:

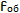
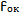
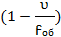
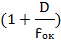
25 см для большинства людей), и — фокусное расстояние линз объектива и окуляра. Величины и обычно называют увеличением объектива и окуляра соответственно.
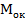
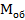
Практическое увеличение микроскопа определяется произведением увеличения окуляра на увеличение объектива .

Практическая часть

Цель работы: Определение плотности дислокаций монокристалла кварца методами оптической микроскопии.
Оборудование: Металлографический микроскоп МЕТАМ

Таблица результатов

Источник

• ← Что такое стояночные огни в автомобиле
• Что такое гипермедиа в информатике →

Образец	Изображение	Измерения
1