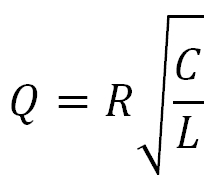Что такое волновое сопротивление резонансного контура
Волновое сопротивление линии
Волновое сопротивление — один из параметров электропроводящей линии, состоящей из металлических проводников. Оно показывает, какое сопротивление оказывает линия источнику энергии (генератору). Этот параметр необходимо учитывать при создании различных электрических схем, чтобы избежать значительных потерь энергии.
Природа волнового сопротивления
Волновое сопротивление линии передачи определяется отношением напряжения к току в электромагнитной волне, распространяющейся вдоль линии передачи. Оно является характеристикой среды распространения электромагнитной волны. Волновое сопротивление любого проводника не зависит от его длины, сопротивления нагрузки на линии и выходного сопротивления источника напряжения. Оно определяется лишь конструктивными параметрами сечения передающих проводников.
Для коаксиальных кабелей такими параметрами являются диаметры центрального и внутреннего проводников, а также значение диэлектрической постоянной материала заполнителя. Для линии, состоящей из двух проводов, — это расстояние между проводами, их диаметр и характеристики материала, используемого для заполнения пространства между ними.
Численно волновое сопротивление равно входному сопротивлению бесконечно длинной линии с конечной нагрузкой, равной ее собственному волновому сопротивлению. Измеряется оно в Омах и показывает, в каком соотношении находятся электрическая и магнитная составляющие электромагнитной волны.
Несмотря на то, что ток по проводнику распространяется практически мгновенно, любой электрический провод или кабель обладает волновым сопротивлением. Обычный электрический провод включает два проводника, изолированные друг от друга. Если проверить омическое сопротивление между ними, оно будет бесконечным. Если при помощи омметра проверить его, подключившись к разным концам одного проводника, то станет видно, что оно нулевое.
На маркировке кабеля указывается его импеданс (сопротивление). В большинстве обычных ситуаций он примерно равен 50 или 75 Ом. Если воспользоваться омметром, будет получен результат, о котором было рассказано выше. Важно понимать, что на самом деле речь идёт не об омическом, а о волновом сопротивлении.
Виды сопротивлений в электрических цепях
В электроцепях существует три вида сопротивлений, имеющих разную природу:
Активное сопротивление
Напряжение, приложенное к электрической цепи, создаёт ток, сила которого пропорциональна имеющейся разнице потенциалов. Коэффициент пропорциональности между ними является активным сопротивлением, которое также называют омическим. Когда в приведённом выше примере измерение проводилось омметром, то речь шла именно о таком сопротивлении. Величина активного сопротивления определяется из закона Ома.
Реактивное сопротивление
Если в цепи присутствует ёмкость, то возникает такой вид сопротивления, как емкостное. Оно равно нулю в том случае, когда ток постоянен. Ёмкостное сопротивление проявляется в цепи переменного тока, а также в тех случаях, когда между деталями нет прямого контакта.
Действие этого сопротивления основано на том, что расположенные рядом, но не имеющие непосредственного соединения проводники накапливают электрические заряды до определённой предельной величины, а затем постепенно разряжаются. При этом возникающий ток направлен противоположно его первоначальному изменению.
Это свойство используется в конденсаторах. Однако нужно учитывать, что ёмкость возникает практически в любых расположенных рядом проводниках, по которым течёт ток. В частности, это относится к двум жилам, из которых состоит электрический провод. В результате любое изменение силы тока в них обеспечит возникновение емкостного сопротивления.
Также существует индуктивное сопротивление. При изменениях напряжения создаётся переменное электромагнитное поле, которое индуцирует ток. Он всегда направлен противоположно первоначальному изменению. То есть, увеличивающееся индукционное сопротивление создает ток, который тормозит первоначальное изменение и наоборот.
Этим свойством обладают катушки индуктивности, но практически любые электрические детали имеют индуктивность, которая действует указанным образом. Это относится также к электрическим проводам. Они имеют определённую индуктивность, которую можно определить, поэтому оказывают сопротивление переменному току. Индуктивное сопротивление возникает также при включении или выключении нагрузки в цепи постоянного тока.
Разницу емкостного и индуктивного сопротивлений называют реактивным сопротивлением.
Импеданс
При определении импеданса или полного сопротивления учитываются все три физические разновидности сопротивления. С этой целью используют прямоугольный треугольник, у которого длина одного катета выражает значение активного сопротивления, а другого — разницу между величинами емкостного и индуктивного сопротивления.
Гипотенуза в этом случае является полным сопротивлением. Его можно определить, воспользовавшись теоремой Пифагора.
Практически в любой электрической цепи присутствуют все виды сопротивления. Однако некоторые из них могут быть пренебрежимо малы. При рассмотрении двух жил, составляющих электрический провод, учитывается лишь емкостное и индуктивное сопротивление. Следовательно, их полное сопротивление будет выражаться лишь реактивной составляющей. В этом случае можно сказать, что волновое сопротивление — это импеданс в кабеле. Он учитывает емкостную и индуктивную нагрузки.
Волновое сопротивление проводов
Если представить себе провод бесконечной длины, состоящий из двух жил и подключённый к источнику питания, то можно заметить, что не только переменный ток, но и постоянный в моменты включения и выключения создаёт волновое сопротивление.
В момент включения распространение тока по проводам будет иметь очень большую скорость, но, тем не менее, конечную. При этом в первые доли секунды ток можно рассматривать как переменный. Так как расположенные рядом провода условно являются пластинами конденсатора, начнётся процесс зарядки ёмкости, что обеспечит возникновение емкостного сопротивления.
Оба провода имеют индуктивность. Она пренебрежимо мала по сравнению с тем, какая у катушки, но она существует. Это в момент включения порождает индуктивное сопротивление. На самом деле получающийся импеданс можно измерить. Именно он представляет собой волновое сопротивление кабеля или провода.
Это относится к различным видам кабелей и справедливо как для многожильных, так и для коаксиальных кабелей. Предположение о значительной длине провода позволяет не рассматривать наложение на распространяющуюся волну отражённых волн. Расчет волнового сопротивления выполняется по специальным формулам.
Формулы для расчёта
Для двухпроводной электролинии без потерь значение внутреннего сопротивления рассчитывается по формуле:
Поскольку при определении волнового сопротивления используется понятие бесконечного проводника, имеющего идеальную форму, то для расчёта применяются формулы, учитывающие геометрические особенности и материал проводников. Далее приведены те, которые применяются в наиболее простых случаях.
Если рассматривается электропровод, состоящий из двух жил, то волновое сопротивление определяется по формуле:
При использовании коаксиальных кабелей формула будет выглядеть таким образом:
Практическое использование волнового сопротивления
Зная эту характеристику, можно предвидеть, какое будет полное сопротивление при пропускании тока высокой частоты через кабель. Чем волновое или полное сопротивление выше, тем меньше он приспособлен работать с высокой частотой. Поэтому в каждом случае использование определённого кабеля подразумевает определённые требования к волновому сопротивлению кабеля.
На практике наибольшее распространение получили коаксиальные кабели с сопротивлением 50 Ом. Это связано с тем, что они способны обеспечить передачу радиосигналов с наименьшими потерями по мощности. Применение коаксиальных кабелей 75 Ом в телевидении объясняется таким их достоинством, как наименьшее ослабление сигнала, что для телевизионного приемника является необходимым условием.
Волновое сопротивление очень важно при использовании сложных систем. Обычно его подбирают таким образом, чтобы оно соответствовало характеристикам платы, заземления и другим особенностям оборудования. Смысл волнового сопротивления подразумевает, что при использовании кабеля с неподходящей характеристикой поведение устройства может стать непредсказуемым.
Рассматриваемая характеристика измеряется для идеального провода. Он, в частности, должен не иметь изгибов, неровностей, скручиваний и аналогичных особенностей. Каждая из них нарушает идеальность распространения волны вдоль проводника, создаёт искажения и отражения. Эти изменения могут существенно влиять на электрические параметры кабеля, чего нельзя допускать. При использовании волнового сопротивления такие отклонения должны быть учтены.
Нужно также учитывать затухание сигнала, которое происходит при его реальном прохождении через проводник. Его величина будет зависеть от используемой частоты.
Когда используется электрическая энергия, важно, чтобы система обладала максимальным коэффициентом полезного действия. Одним из важных условий для этого является равенство трёх сопротивлений – передатчика, приёмника и линии передачи. Рассогласование между ними приводит к потере энергии и соответствующему снижению КПД.
Что делать, если не указано волновое сопротивление
При использовании кабеля важны все его характеристики. Однако нельзя исключить ситуацию, когда в руки попадает такой, волновое сопротивление которого остаётся неизвестным.
В этом случае нужно воспользоваться соответствующей формулой. Сказанное будет пояснено на примере. Выше была приведена формула расчёта для коаксиального кабеля. Мастер, взяв его в руки, понял, что были использованы следующие материалы:
Расстояние от провода до оболочки равно 7.5 мм. Толщина провода составляет 2.7 мм. Используемый коэффициент выражает свойства используемого изолятора. Для пористого полиэтилена он составляет 1.5.
Если бы для изоляции применялся обычный полиэтилен, коэффициент был бы равен 2.5, а для ПВХ — 3.5.
Чтобы получить ответ, необходимо подставить имеющиеся значения в формулу. Таким образом, можно подсчитать:
138/√1.5 × (log(7.5мм/2.7мм) = 49.9 Ом.
В формуле расчета волнового сопротивления учитываются и погонное сопротивление проводов, и погонное сопротивление изоляции между ними. Но на высокой частоте эти факторы оказывают на волновое сопротивление настолько незначительное влияние, что ими вполне можно пренебречь.
Если же сопротивление нагрузки равняется волновому сопротивлению линии, то через кабель заданного диаметра можно передать максимальный уровень мощности с наименьшими потерями.
Видео по теме
Параллельный колебательный контур
В прошлой статье мы с вами рассмотрели последовательный колебательный контур, так как все участвующие в нем радиоэлементы соединялись последовательно. В этой же статье мы рассмотрим параллельный колебательный контур, в котором катушка и конденсатор соединяются параллельно.
Параллельный колебательный контур
Идеальный колебательный контур
На схеме идеальный колебательный контур выглядит вот так:
Реальный колебательный контур
В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема реального колебательного контура примет вот такой вид:
R — это сопротивление потерь контура, Ом
L — индуктивность, Генри
Принцип работы параллельного колебательного контура
Давайте подцепим к генератору частоты реальный параллельный колебательный контур
Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.
Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.
Реактивное сопротивление катушки выражается по формуле
а конденсатора по формуле
Более подробно про это можно прочитать в этой статье.
Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки XL и конденсатора XC уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.
Резонанс параллельного колебательного контура
Очень интересное свойство параллельного колебательного контура заключается в том, что при ХL = ХС у нас колебательный контур войдет в резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:
Rрез — это сопротивление контура на резонансной частоте
C — собственно сама емкость конденсатора
R — сопротивление потерь катушки
Формула резонанса
Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:
F — это резонансная частота контура, Герцы
L — индуктивность катушки, Генри
С — емкость конденсатора, Фарады
Как найти резонанс параллельного колебательного контура на практике
Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.
Итак, реальная схема этого контура будет вот такая:
Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:
На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.
Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура Rкон.
Упрощенная схема будет выглядеть вот так:
Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление Rкон будет максимальным, вследствие чего у нас на этом сопротивлении «упадет» бОльшее напряжение.
Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.
Как вы видите, на колебательном контуре «падает» малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление Rкон
Добавляем частоту. 11,4 Килогерца
Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.
Добавляем еще частоту. 50 Килогерц
Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.
Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.
И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.
Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:
Снова добавляем частоту и видим, что напряжение стало еще меньше:
Что происходит на резонансной частоте в параллельном колебательном контуре
Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.
Что здесь у нас произошло?
Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое высокое сопротивление Rкон. На этой частоте ХL = ХС. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:
Резонанс токов
Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:
Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:
Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.
Добротность параллельного колебательного контура
Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз. Q — это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила тока в контуре Iкон больше сила тока в общей цепи Iрез
Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:
R — сопротивление потерь на катушке, Ом
Применение параллельного колебательного контура
Параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры.