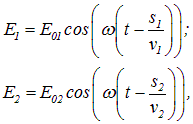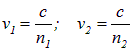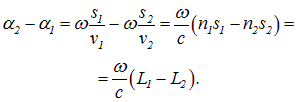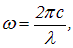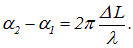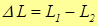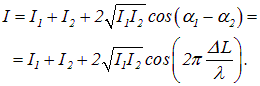Что такое волновой цуг

Цуг волн

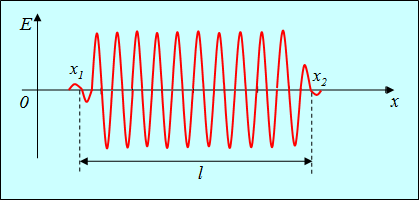
Цуг волн — это ряд возмущений с перерывами между ними. Излучение отдельного атома не может быть монохроматическим, потому что излучение длится конечный промежуток времени,имея периоды нарастания, установления и процесс угасания.

Его [цуг] можно представить суперпозицией гармонических волн частотного диапазона (ω±Δω/2):

Цуг волн может принимать участие в создании картины интерференции при условии, что сдвиг фаз между центрами частотного диапазона и его пределом не превышает , то есть, чтобы колебания от центра не уничтожались колебаниями от других составляющих цуга:

Предельное значение позволенного времени называется временем когерентности цуга, а расстояние, определяющееся временем когерентности, называется длиной когерентности цуга и вычисляется следующим образом:

где c=скорость волны.

Литература

Полезное

Смотреть что такое «Цуг волн» в других словарях:

цуг волн — 2.2.11 цуг волн: Последовательность определенного числа ультразвуковых волн, исходящих от одного источника, имеющих одинаковый тип и распространяющихся в одном направлении. Источник: ГОСТ Р ИСО 5577 2009: Контроль неразрушающий. Ультразвуковой… … Словарь-справочник терминов нормативно-технической документации

цуг волн — bangų vora statusas T sritis fizika atitikmenys: angl. wave train vok. Wellenzug, m rus. цуг волн, m pranc. train d’ondes, m … Fizikos terminų žodynas

ЦУГ — (нем. Zug). Упряжка лошадей, запряженных попарно или по одной в ряд езда цугом; поезд железной дороги. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЦУГ запряжка гуськом. Словарь иностранных слов, вошедших в… … Словарь иностранных слов русского языка

Цуг — Цуг: Цуг город в Швейцарии, столица одноимённого кантона. Цуг кантон в Швейцарии. цуг вид упряжки, в которой лошади идут гуськом или парами, одна за другой. Цуг швейцарский хоккейный клуб. См. также Цуг волн … Википедия

ГОСТ Р ИСО 5577-2009: Контроль неразрушающий. Ультразвуковой контроль. Словарь — Терминология ГОСТ Р ИСО 5577 2009: Контроль неразрушающий. Ультразвуковой контроль. Словарь оригинал документа: 2.8.2 автоматическое сканирование: Перемещение преобразователя по поверхности ввода, реализованное механическими средствами.… … Словарь-справочник терминов нормативно-технической документации

Волны — Волны: а одиночная волна; б цуг волн; в бесконечная синусоидальная волна; l длина волны. ВОЛНЫ, изменения состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию. Основное свойство всех волн, независимо от их… … Иллюстрированный энциклопедический словарь

Волны — Волна изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой… … Википедия

волновой пакет — цуг волн Последовательность непрерывных упругих волн, исходящих из одного источника и распространяющихся в одном направлении. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное… … Справочник технического переводчика

Интерференция света — Интерференция света опыт Юнга Интерференция света перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве ма … Википедия

Источник

Интерференция света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: интерференция света.

Оказывается, что две лампочки, пусть и совершенно одинаковые, всегда будут некогерентными источниками света. А вот чтобы понять, почему лампочки некогерентны, надо немного поговорить об излучении света атомами.

Волновой цуг.

Откуда вообще берётся свет? Видимый свет излучается атомами различных тел. Механизм излучения света относится квантовой физике, но для понимания оптических интерференционных явлений знать хотя бы в общих чертах, как атомы излучают свет, надо обязательно. Поэтому обсудим вкратце этот вопрос.

Обычным состоянием атома, в котором он может пребывать неограниченно долго, является основное, или невозбуждённое состояние. Когда атом находится в основном состоянии, электроны, окружающие ядро атома, максимально заполняют ближайшие к ядру орбиты. Потенциальная энергия взаимодействия электронов с ядром принимает своё минимальное значение, и говорят, соответственно, что
в основном состоянии атом обладает наименьшей энергией.

Рис. 1. Излучение атомом волнового цуга

Длительность цуга порядка ; соответственно, длина цуга м. Частота цуга может находиться в видимом диапазоне, и тогда цуг будет регистрироваться человеческим глазом.

Ну а теперь самое главное. Из возбуждённого состояния в основное атом переходит в случайный, непредсказуемый момент времени. Это означает, что моменты испускания цугов различными атомами никак не согласованы между собой!

Цуги, образующие свет, даже если и обладают одной частотой, имеют совершенно произвольные начальные фазы и потому являются некогерентными. Вот почему от двух одинаковых лампочек не получается устойчивой интерференционной картины: излучаемые ими пучки света состоят из некогерентных цугов и не могут интерферировать друг с другом.

Зеркала Френеля.

Рис. 2. Интерференционный опыт с зеркалами Френеля

Световые лучи, как всегда, изображены зелёным цветом. Направления лучей мы уже не указываем, чтобы не загромождать рисунок. К тому же, у вас позади геометрическая оптика, так что вы легко поймёте ход лучей и без указания их направления 🙂

Интерференция в тонких плёнках

Глядя на переливающийся различными цветами мыльный пузырь, на радужные отблески масляных или бензиновых пятен на поверхности воды, вы, оказывается, наблюдаете не что иное, как интерференцию света!

Рис. 3. Интерференция в тонкой плёнке

Предположим, что плёнка освещается белым светом. Как вы знаете, белый свет является смесью волн с различными частотами; эти частоты отвечают цветам от красного до фиолетового. Пусть, например, разность хода между волнами и равна целому числу длин волн красного света. Тогда красная составляющая белого света усилит сама себя, и отражённый плёнкой свет нам будет казаться красным.

При небольшом изменении угла падения (или толщины плёнки) изменится и разность хода. Поэтому, если поверхность плёнки является неровной (или если мы посмотрим чуть с другого направления), то новая разность хода может стать равна целому числу длин волн, например, зелёного света. Теперь произойдёт усиление зелёной составляющей белого света, и отражённый от плёнки свет мы увидим зелёным.

Всё это мы наблюдаем, рассматривая мыльный пузырь. Перемещение его поверхности приводит к постоянному изменению разности хода для данного ракурса. Происходит усиление то одного цвета, то другого, и в результате пузырь переливается цветами радуги.

Кольца Ньютона.

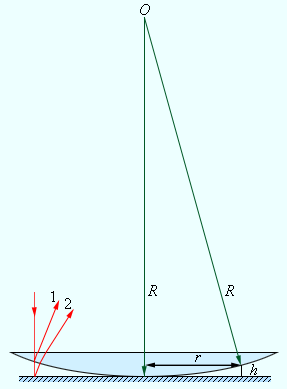
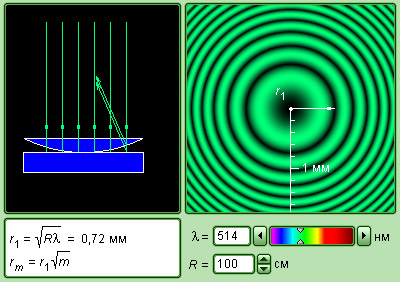
Возьмём плоско-выпуклую линзу с достаточно большим радиусом сферической поверхности и положим её выпуклостью вниз на стеклянную пластину. Если глядеть сверху, то сквозь линзу можно увидеть интерференционную картину в виде концентрических колец (рис. 4 )

Рис. 4. Кольца Ньютона в красном свете

Это кольца Ньютона; они изучались Ньютоном при освещении как белым, так и монохроматическим светом. Происхождение колец Ньютона вполне аналогично интерференции в тонких плёнках (рис. 5 ).

Рис. 5. Происхождение колец Ньютона

Падающий луч расщепляется на два луча 1 и 2, отражённых соответственно от сферической поверхности линзы и от пластины; между этими лучами возникает разность хода, и они интерферируют между собой. Все три луча, изображённые на рисунке, в реальности почти сливаются друг с другом из-за малой кривизны поверхности линзы.

Вычислим радиусы светлых колец Ньютона. Пусть точка падения луча на сферическую поверхность находится на расстоянии y от пластины (рис. 6 ).

Рис. 6. К расчёту радиусов колец

Поскольку воздушная прослойка очень тонка ( ), величиной можно пренебречь по сравнению с :

Рис. 7. Отражение со сдвигом на полволны и без него

Справа на рис. 7 показано отражение на границе стекло-воздух. Изменения фазы нет! И это общий факт:при отражении от оптически менее плотной среды фазы отражённой и падающей волн совпадают.

Светлые кольца будут в местах интерференционных максимумов, когда разность хода равна целому числу длин волн. Имеем:

Отсюда получаем радиусы светлых колец:

Как видим, радиус растёт с увеличением номера кольца. Кроме того, радиус кольца с заданным порядковым номером возрастает при переходе от фиолетового цвета к красному (поскольку увеличивается длина волны).

Просветление оптики.

Пожалуй, самым широким на сегодняшний день применением интерференции света служит просветление оптики. Расскажем вкратце, что это такое.

Свет, падающий на линзу, частично отражается назад; доля отражённого света обычно составляет несколько процентов. Объективы современной оптической техники представляют собой системы линз (числом до нескольких десятков). В результате отражений на поверхности каждой линзы происходит значительное ослабление света: в сумме на отражениях может теряться до 90% световой энергии. Освещённость изображений предметов, даваемых такой оптической системой, будет чрезвычайно низкой.

Как уменьшить потери на отражение? Для этого на поверхность линзы наносят интерференционное покрытие в виде тонкой плёнки (рис. 8 ).

Рис. 8. Просветление оптики

Источник

4.3. Интерференция света от двух источников

Механизм излучения электромагнитных волн заключается в том, что атом, находящийся в возбужденном состоянии, при переходе на более низкий энергетический уровень излучает электромагнитную волну. Процесс излучения длится около 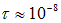с. Таким образом, атом излучает волну, представляющую собой часть синусоиды (см. рис. 4.2), которая называется волновым цугом.

Рис. 4.2. Волновой цуг

Длина волнового цуга в вакууме равна

Естественный свет представляется совокупностью несогласованных между собой цугов волн, испускаемых отдельными атомами. Поэтому невозможно получить интерференцию от двух разных источников естественного света. Для получения когерентных световых волн тем или иным способом разделяют на две части волну, излучаемую одним источником. После прохождения различных оптических путей эти две части одной волны накладываются друг на друга (рис. 4.3).

Рис. 4.3. Разделение волны от естественного источника

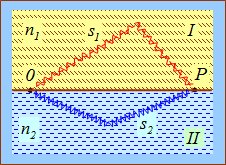
Предположим, что разделение на две когерентные волны происходит в некоторой точке 0, лежащей на границе раздела двух сред I и II. До точки Р в которой наблюдается интерференционная картина, одна волна проходит путь s₁ в среде с показателем преломления п₁, а вторая волна — путь s₂ в среде с показателем преломления п₂. Если начальные фазы обеих волн равны нулю, то в точке Р волны возбудят колебания

— фазовые скорости первой и второй волн соответственно. Разность фаз колебаний в точке Р равна

Выражая циклическую частоту через длину волны l в вакууме

Оптическая разность хода — это разность

оптических длин путей, проходимых волнами.

Запишем интенсивность результирующей волны в точке Р в виде

Когда оптическая разность хода равна целому числу длин волн в вакууме (или, что то же самое, четному числу полуволн), то есть

колебания в точке Р находятся в одинаковой фазе, 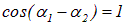и наблюдается интерференционный максимум.

Если оптическая разность хода равна нечетному числу полуволн, то есть

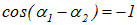
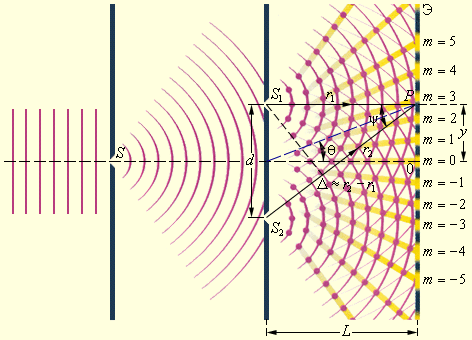
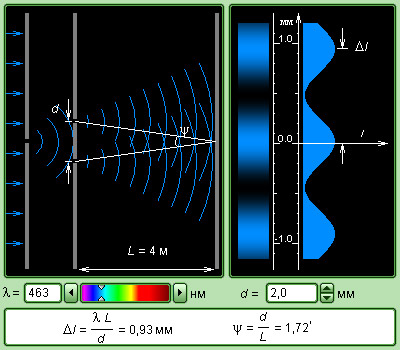
то колебания, возбуждаемые в точке Р обеими волнами, находятся в противофазе, и наблюдается интерференционный минимум.

Установив общие закономерности, обратимся к конкретному примеру интерференции, когда источниками света служат две узкие параллельные щели, расположенные достаточно близко друг к другу. Пусть эти щели S₁, и S₂ находятся на расстоянии d друг от друга (рис. 4.4).

Рис. 4.4. Интерференция от двух когерентных источников света

Интерференция наблюдается в некоторой точке Р экрана, расположенного на расстоянии l от источников света (l>>d, 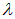). Начало отсчета на оси 0х выбрано в точке 0, симметричной относительно щелей.

Интенсивность в точке Р, расположенной на расстоянии x от начала отсчета, определяется оптической разностью хода, которая в данном случае (п = 1) равна геометрической разности хода

Источник

Начала физики. 32. Волновые пакеты. Неопределенности и принцип Гайзенберга на пальцах.

1. Корпускулярно-волновой антропоцентризм.
Наши мозги и язык всегда в той или иной степени идеализирует реальность. Когда мы говорим о волнах, то представляем себе, как правило, бесконечно длинную волну постоянной амплитуды с одинаковыми расстояниями между горбами волны. Но реальность не такова. Волны всегда образуют волновые пакеты (цуги волн). Примерно такие:

С большим или меньшим числом волновых горбов внутри пакета.

Кто и как будет воспринимать такой волновой пакет? В начале прошлого века связь и вещание велись на длинных (километры) и средних (сотни метров) электромагнитных волнах. И мы их назвали радиоволнами. Терминология не изменилась при переходе на короткие (десятки метров), ультракороткие (метры) и дециметровые (сотовая связь) волны. Но уже при переходе на диапазон длин волн от миллиметра до микрометра мы уже говорим об инфракрасном излучении, но не о волнах. А для обозначения более коротковолных диапазонов (начиная от видимого света на длинах волн

400-700 нанометров) пользуемся терминами фотоны и кванты. Подразумевая, тем самым, что пакеты таких волн мы воспринимаем как частицы.

Итак, понятие корпускулярно-волнового дуализма в немалой степени антропоцентрично. Поэтому вас не должен удивлять тот факт, что физики при описании многих коллективно-волновых явлений в сплошных стредах стали вводить понятия квазичастиц. Таких, как фононы, являющиеся по сути волновыми пакетами (квантами) колебаний кристаллических решеток в твердых телах.

2. Неопределенности и принцип Гайзенберга.
Тот факт, что волновой пакет имеет конечную длину Δ х, означает, что в таком пакете есть приличная примесь волн, длина которых отличается от основной, и которые в конечном счете гасят колебания ξ(x,t) на краях пакета. Это можно описать как наличие в пакете заметной примеси длин волн в диапазоне Δ λ в окрестности основной длины волны. Или примеси волн с волновыми числами k = 2 π/ λ в диапазоне Δk в пакете:

Но ведь это не что иное, как соотношение неопределенностей Гайзенберга! Надеюсь, такая проверка удовлетворит самых взыскательных читателей.

3. Наблюдение принципа неопределенности Гайзенберга с пригорка у моря.
Вытекающий из соотношения (3) принцип неопределенности Гайзенберга часто трактуют следующим образом. Если мы попытаемся своим прибором измерить пространственную координату частицы (пакета волн) с погрешностью в пределах Δ х, то в результате такого измерения компонента импульса частицы вдоль той же координаты (компонента волнового числа) станет неопределенной в рамках Δp

1 / Δ х). Продемострируем это утверждение картинкой, которую многие из нас могли наблюдать на берегу моря:

Из этой картинки видно, что если мы ограничиваем (измеряем) волну вдоль координаты, параллельной передней стенке мола, проходом ширины dx, то в том же направлении возникает неопределенность волнового вектора K на величину dk. Что выражается в искривлении фронта вошедшей внутрь мола волны.

4. Волны де Бройля.
Предтечей соотношения неопределенностей Гайзенберга явилась ничуть не противоречащая ему гипотеза де Бройля, предписывающая каждой имеющей массу частице длину волны

Его в качестве шутливого примера можно применить и к идущему по улице человеку. В системе отсчета домов, мимо которых он проходит, длина волны де Бройля человека λ дБ

Источник

Интерференция световых волн

Интерференция – это одно из наиболее ярких проявлений волновой природы света. Мы можем наблюдать такое интересное и красивое явление, если наложить друг на друга 2 или более световых пучков. В месте перекрывания пучков интенсивность волны света обладает характером чередующихся светлых и темных полос, при этом в точках максимумов интенсивность больше, а в точках минимумов меньше суммы интенсивностей пучков.

При белом свете интерференционные полосы окрашиваются в разные цвета светового спектра. На практике интерференционные явления окружают нас повсюду. Это и цвета масляных пятен на асфальте, и окрашивание замерзающих оконных стекол, и чудесные цветные рисунки на крыльях отдельных бабочек и жуков.

Первый научный эксперимент проявления интерференции света

Интерференционный опыт Юнга

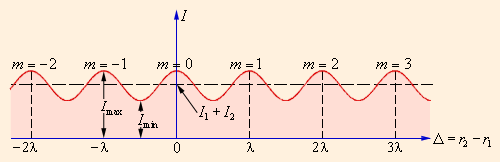
Путем простых тригонометрических вычислений можно прийти к следующему выражению для интенсивности результирующего колебания в точке P :

где Δ = r 2 – r 1 – это разность хода.

Подчеркнем, что в волновой оптике понятие “луч света” теряет физический смысл в отличие от геометрической оптики. Определение «луч» в волновой оптике употребляется для краткости обозначения направления распространения волны.

Далее данный термин будет упоминаться без кавычек.

По данной формуле рассчитывается длина световой волны λ при известном радиусе кривизны R линзы.

Проблема когерентности волн

Источник