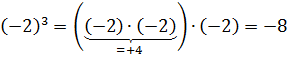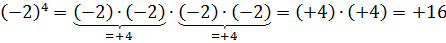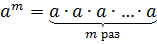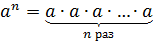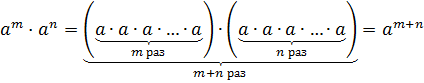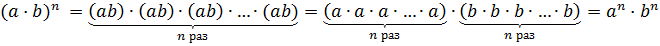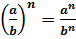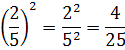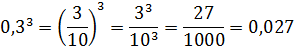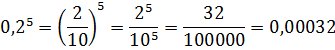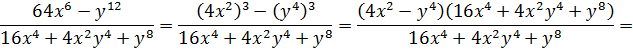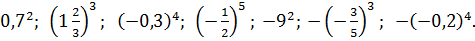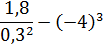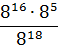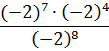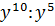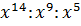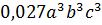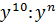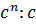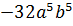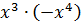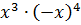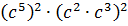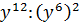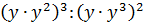Что такое возведение в степень в математике

Возведение в степень: правила, примеры

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Решение

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Решение

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Как возвести число в целую степень

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Решение

Решение

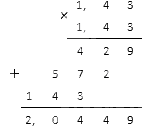
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

Как возвести число в дробную степень

Проиллюстрируем на примере.

Решение

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Решение

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Вычислите приближенное значение 2 в степени 1,174367.

Решение

Источник

Что такое степень числа

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Исключение составляют записи:

Конечно, выражения выше можно читать и по определению степени:

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Квадрат любого числа есть положительное число или нуль, то есть:

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

Пример. Вычислить: −6 2 − (−1) 4

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Источник

Свойства степеней. Действия со степенями

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

a — основание степени;

n — показатель степени.

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Источник

Степень с натуральным показателем

Что такое степень?

Степень с натуральным показателем. Как возвести в степень?

Для ответа на вопрос, что такое степень, для начала вспомним, что такое обычное умножение. По своей сути.)

Например, надо нам найти сумму четырёх одинаковых слагаемых:

Значит, умножение (любое) на натуральное число n – это просто сложение n одинаковых слагаемых.

И тут ленивые математики не захотели каждый раз возиться, выписывая n одинаковых множителей подряд. И тоже придумали отдельное название для такого произведения — степень.

Согласитесь, что так обозначать степень куда удобнее и компактнее, чем в лоб писать что-то вроде

Причём ладно, если множителей немного — 3 или 10 там. А если 100? Или 1000? Вот и пришлось вводить отдельное краткое обозначение для степени, не зависящее от хотелок математиков.)

2 5 = 2·2·2·2·2 = 32 (произведение пяти двоек или «два в пятой степени»);

4 3 = 4·4·4 = 64 (произведение трёх четвёрок или «четыре в третьей степени»).

Обратим внимание, что степенью называется именно произведение одинаковых множителей. Если хотя бы один из множителей от остальных отличается, то степенью такое произведение в целом назвать уже нельзя.)

Откуда взялись такие особые названия для второй и третьей степени? Из… геометрии. 🙂

Назовём их а и b.

Тогда площадь прямоугольника, как мы знаем, считается как произведение длины и ширины или просто ab.

А что же происходит со сторонами, когда наш прямоугольник превращается в квадрат? Да! Длина и ширина становятся равны (так как у квадрата, как известно, все стороны равны :-)). И что же тогда произойдёт с нашей площадью (площадью теперь уже не прямоугольника, а квадрата)? Раз а и b у нас стали равны, то площадь нашего квадрата станет равна произведению

Теперь поговорим о показателе. Слово «натуральный» в заголовке не зря написано. 🙂 Почему же показатель называется натуральным? Чего в нём такого уж натурального-то? 🙂

Что такое первая степень числа?

Особняком стоит такое, очень часто встречающееся в математике понятие, как первая степень числа.

Работаем с отрицательными числами.

Отрицательные числа приходится возводить в степень постоянно. Не реже положительных. 🙂 И главным источником дурацких ошибок при работе с ними является, как вы уже, наверное, догадываетесь, путаница в знаках. Есть смысл разобраться, правда?

Для начала посчитаем вот такую степень: (-2) 2

Всё точно так же. Берём и умножаем минус двойку саму на себя:

Получили четыре. С каким знаком? С плюсом! Ибо минус на минус всегда даёт плюс. А вот это уже очень важно. 🙂

А теперь возведём минус двойку в другую степень. В куб. 🙂

Получили восьмёрку. С минусом! Минус восемь. Почему так произошло? Потому, что при перемножении трёх отрицательных чисел два минуса дали нам плюс, а вот для третьего минуса уже не оказалось пары. 🙂 И именно этот «лишний» минус и сделал нам всё произведение отрицательным. 🙂 Смотрите сами:

Идём дальше. Считаем четвёртую степень:

Здесь для каждого минуса нашлась пара. Поэтому вся степень — положительная. 🙂

И так далее. Эту славную цепочку можно продолжать до бесконечности… Но не нужно. 🙂 Самые наблюдательные, возможно, уже заметили: при возведении отрицательного числа в чётную степень всегда будет получаться положительное число, а при возведении в нечётную — отрицательное. Респект наблюдательным. 🙂 Совершенно верно! Отсюда правило: отрицательное число в чётной степени даёт положительное число, а в нечётной — отрицательное.

Здесь пока всё понятно. Но чуть выше я уже упоминал про ошибки в знаках. Где же чаще всего народ ошибается? А типичная ошибка здесь случается вот какая. Решим эту проблемку. Для этого рассмотрим два выражения:

Уловили разницу? Поэтому, чтобы не косячить в знаках, внимательно следим за тем, сам минус целиком у нас возводится в степень или же минус ставится перед степенью. Отличительная черта — скобочки. И тогда ошибок в знаках не будет. 🙂

Правила действий со степенями. Умножение степеней.

Для начала посчитаем вот такое выражение:

Скобки при перемножении одинаковых двоек сути дела не меняют. Поскольку кроме умножения других действий здесь просто нет.) Поэтому скобки со спокойной душой можно опустить:

(2 · 2) · (2 · 2 ·2) = 2 · 2·2·2·2

А теперь анализируем: каким образом у нас образовалась пятёрка в показателе? Не вопрос: мы сложили показатели 2 и 3 у множителей. И получили, знамо дело, пятёрку в журнал.) То есть,

2 2 ·2 3 = 2 2+3 = 2 5 = 32.

И так будет получаться всегда при любом перемножении степеней с одинаковым основанием. Отсюда правило произведения степеней: при перемножении степеней с одинаковыми основаниями показатели степеней складываются:

Например, 3 4 ·3 2 = 3 4+2 = 3 6 = 729.

Собственно, а как в общем виде понять, почему так получается? В математике большинство утверждений принято доказывать.) Для двойки мы правило уже доказали. На частном примере. А вдруг, при каких-то других числах оно справедливо уже не будет? Проверим.)

Вот и всё, никаких хитростей.) Данное правило справедливо для любого количества множителей. Лишь бы основания были одинаковыми (это важно!):

Внимание! Типичные (и очень грубые) ошибки!

Во-первых. Для применения данного правила основания степеней должны быть одинаковыми! Я не зря ещё раз занудно выделяю это слово. 🙂 Попробуем, к примеру, применить его, когда основания разные:

3 4 ·2 5 = (. ) 4+5 = (. ) 9

Так, показатели мы сложили. Ну а дальше что? Что писать в итоговое основание будем? Двойку? Тройку? Или, может быть, шесть? Непонятно…

Именно поэтому для применения данного правила основания степеней и должны быть одинаковыми.)

Во-вторых. Сами степени между собой должны именно перемножаться, а не складываться! Это показатели в них мы складываем. Но степени между собой перемножаются. Не зря правило называется «произведение степеней«.

Скажем, в выражениях типа 3 2 + 3 4 + 3 5 или a 2 + a 3 + a 4 показатели складывать уже нельзя! Не имеем права. 🙂 Именно по той простой причине, что сами степени у нас связаны между собой знаком «плюс», а не умножением. Хотя основания и одинаковые, но плюс здесь всё испортил. 🙂

Переходим теперь к делению степеней.

Правила действий со степенями. Деление степеней.

А теперь проанализируем наш результат. Что такое 4 как степень двойки? Два в квадрате, верно? Значит, наше деление можно записать вот так:

Теперь снова анализируем показатели. У делимого показатель пятёрка, у делителя — тройка, а у частного — двойка. То есть, разность показателей делимого и делителя: 5 — 3 = 2. Значит,

Итак, при делении двух степеней с одинаковыми основаниями показатели степеней делимого и делителя вычитаются:

Ну, логично: если при перемножении степеней мы показатели складывали, то при делении их тогда надо уже вычитать. Потому что деление — это операция, обратная умножению. 🙂

Здесь одно важное (пока что, на нашем уровне) ограничение: показатель степени делимого должен быть больше показателя степени делителя: m > n.

В самом деле, что будет, например, если мы попробуем найти вот такое частное:

Что такое нулевая степень числа?

А вот степень с нулевым показателем, пожалуй, рассмотрим уже сейчас, наряду с натуральными показателями. Для этого вновь выпишем нашу формулку деления степеней:

Ведь мы, возводя в степень, повторяем число множителем два, три и т.д. раз. Но что же значит, повторить число множителем ноль раз? Непонятка! Если подходить к понятию степени с нулевым показателем так же, как и к степени с обычным натуральным показателем: ноль ведь не является натуральным числом!)) Как нам быть?

Итак, нулевая степень любого не равного нулю числа равна единице:

Например, 2 0 = 3 0 = 100 0 = 1234 0 = (-1) 0 = (-337) 0 =…=1

Степень произведения. Степень частного.

Степень произведения равна произведению степеней множителей :

Ну, давайте посмотрим, почему же так получается. Так получается просто в силу переместительного свойства умножения. 🙂 Смотрите сами:

Это правило позволяет легко и быстро как возводить в степень произведение, так и наоборот — представлять произведение одинаковых степеней в виде единой степени. Например,

(2·3) 2 = 2 2 ·3 2 = 4·9 = 36

И так далее. Идея, думаю, понятна. Рассмотрим теперь возведение в степень частного. То есть, дроби. Здесь всё аналогично.)

Степень частного (дроби) равна частному степеней делимого и делителя (числителя и знаменателя):

(a : b) n = a n :b n или

(6:3) 2 = 6 2 :3 2 = 36:9 = 4

Возводить в степень частное через две точки приходится крайне редко, а вот дроби — сплошь и рядом.

А если дробь десятичная? Никаких проблем! Переводим её в обычную и — вперёд! Например,

Кстати, при возведении в степень десятичных дробей не стоит их тут же рваться сокращать при переходе к обычным: самим же будет проще записывать ответ в десятичной форме. Поэтому так и оставляем в знаменателе 10, 100 и так далее. 🙂 Например,

А вот, если бы мы дробь 2/10 до возведения сократили и записали бы как 1/5, то после возведения у нас получилась бы дробь 1/3125, которую потом переводить в десятичную делением «уголком» – не подарок. Поэтому и не делаем лишней работы. 🙂

Что она означает? Она означает, по-русски, квадрат в кубе. Или, по-математически, степень в степени: мы возводим квадрат числа a в куб.

( a 2 ) 3 = a 2 ·a 2 ·a 2

А вот теперь вспоминаем правило перемножения степеней с одинаковым основанием (самое первое правило).

( a 2 ) 3 = a 2+2+2 = a 6

( a 2 ) 3 = a 2+2+2 = a 2·3 = a 6

И так будет получаться всегда при возведении любой степени в степень.

При возведении степени в степень показатели степеней перемножаются :

Применение данного свойства слева направо даёт нам возможность в уме возводить степень в степень и упрощать всевозможные выражения со степенями:

А вот обратное применение формулы (справа налево) резко расширяет наши математические возможности. А именно — оно позволяет представлять какое-либо выражение в виде степени другого выражения. А это, между прочим, поважнее простого возведения в степень будет. Сомневаетесь? Зря. Когда познакомитесь с разложением многочленов на множители и упрощением дробно-рациональных выражений, то этот приём вы ещё не раз вспомните.

Например, такое задание (для тех, кто повторяет):

Разложить на множители по формуле разности квадратов:

Или вот такой навороченный пример, для старшеньких:

Здесь то же самое выражение 64x 6 — y 12 следует рассматривать уже как разность кубов:

64x 6 — y 12 = (4x 2 ) 3 — (y 4 ) 3

Если теперь воспользоваться формулой разности кубов, да разложить числитель на множители, то вся наша жуткая дробь славненько сократится и упростится:

Эффект здоровский, правда? Если уметь какое-либо выражение превращать в степень. При необходимости.)

Итак, с возведением в степень мы разобрались. Работать со степенями — научились. А теперь — делаем несложные задания. А вы как думали?

Найдите значение выражения:

Представьте в виде степени:

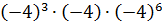
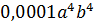
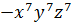
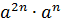
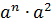
Всё получилось? Поздравляю! Значит, вы поняли, что такое степень и как с ней работать. Не всё получилось? Следим за знаками! 🙂 И сокращать не забываем.

Источник