Что такое временной ряд в эконометрике
Временные ряды эконометрики
Вы будете перенаправлены на Автор24
Элементы временного ряда
Временной ряд – это расположенные последовательно в хронологическом порядке показатели, которые характеризуют развитие того или иного явления во времени.
Основные задачи эконометрического исследования временных рядов:
Характеристиками временного ряда являются:
Значение уровня ряда зависит от влияния на него всей совокупности возможных факторов, которые можно подразделить на группы:
Тип связи между компонентами определяет вид модели, которая может быть аддитивной (сумма компонент) и мультипликативной (произведение компонент).
Определение структуры временного ряда
Готовые работы на аналогичную тему
Чтобы определить состав компонентов в модели временного ряда, необходимо построить автокорреляционную функцию.
Автокорреляцией является корреляционная связь последовательных уровней одного и того же динамического ряда. Таким образом, автокорреляция представляет собой связь между рядами
После расчета коэффициентом автокорреляции, определяется величина лага, при котором наиболее высокая автокорреляция, тем самым выявляется структура временного ряда:
Если ни один из коэффициентов не оказался значимым, то можно сделать один из двух выводов:
Одномерный временной ряд
Временные ряды, которые характеризуют динамику исследуемого явления, имеют большое различие с перекрестными данными, представляющими в статистике экономические явления. Основными отличиями являются:
Все перечисленные особенности временных рядов обуславливают характерные только для них способы статистической обработки. Основными составляющими временного ряда являются: трендовая компонента, сезонная, циклическая и случайная.
Элементы временных рядов могут не представлять действие одновременно четырех факторов: при разных условиях применяются разные комбинации, однако, случайная компонента является обязательной для любых ситуаций.
Временные ряды в эконометрике
Понятие о временном (динамическом) ряде и его структура. Расчёт коэффициента автокорреляции динамического ряда. Моделирование сезонных и циклических колебаний временного ряда. Понятие о динамических эконометрических моделях. Суть методов Алмон и Койка.
| Рубрика | Экономико-математическое моделирование |
| Вид | учебное пособие |
| Язык | русский |
| Дата добавления | 08.11.2013 |
| Размер файла | 904,4 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
временной динамический ряд автокорреляция
Временным рядом называется последовательно расположенные в хронологическом порядке показатели, характеризующие развитие явления во времени.
Основными задачами эконометрического исследования временного ряда является:
1) прогнозирование будущих (недостающих) уровней динамического ряда;
2) изучение взаимосвязей двух и более временных рядов.
Временной ряд характеризуется двумя параметрами:
1) моментами времени (конкретными датами) или периодами (годы, кварталы, недели и т.д.), к которым относятся статистические данные.
Величина уровня ряда определяется влиянием на него всех возможных факторов, которые подразделяют на следующие группы:
2) факторы, формирующие циклические колебания ряда (циклическую компоненту). Циклическая (периодическая) компонента может быть:
Уровень временного ряда будет функция от трендовой циклической и случайной компонент:
В зависимости от вида связи между этими компонентами модель может быть:
1) аддитивная (как сумма компонент)
2) мультипликативная (как произведение компонент)
1.2 Автокорреляция уровней временного ряда. Выявление структуры динамического ряда
Естественно, что при наличии во временном ряду трендовой или циклической компоненты значение каждого последующего уровня будет зависеть от влияния предыдущих уровней
Данная корреляционная зависимость между уровнями временного ряда называется автокорреляцией уровня временного ряда.
Количественно автокорреляцию определяют, рассчитывая коэффициент автокорреляции его можно рассчитать как:
Для того чтобы, определить структуру временного ряда, необходимо найти лаг при котором коэффициент автокорреляции будет наибольшим.
3. Если все коэффициенты автокорреляции не являются статистически значимыми, это может быть обусловлено двумя причинами:
· взаимосвязь между уровнями временного ряда не является линейной;
Коэффициент автокорреляции имеет следующие важные свойства:
1. Коэффициент автокорреляции характеризует тесноту только линейной связи текущего и предыдущего уровней временного ряда. Если временной ряд имеет сильную нелинейную тенденцию, коэффициент автокорреляции будет приближаться к нулю.
2. Знак коэффициента автокорреляции не указывает на возрастающую или убывающую тенденцию временного ряда.
Пример 26. Имеются данные о товарообороте (млн. руб.) за 9 лет, (табл. 54). Рассчитать коэффициенты автокорреляции.
Временные ряды в эконометрических исследованиях
Вы будете перенаправлены на Автор24
Понятие временных рядов
Временной ряд – это статистические данные о неком объекте либо явлении, собранные в разные моменты времени.
Статистика является одним из инструментов исследования и анализа в экономике. Она позволяет рассматривать большие объемы данных с целью выявления закономерностей. Кроме того, существует возможность анализировать большие массивы данных с помощью выборки, которая отражает свойства рассматриваемой совокупности.
В статистическом ряду каждой единице присваивается значение, называемое отсчетом. Временные ряды часто называют рядами динамики, в которых исследуются уровни. Для каждого отсчета указывается время и порядковый номер. Отмечается то время, когда был проведен отсчет. Отличительной особенностью временного ряда является взаимосвязь параметров уравнения со временем. В обычной выборке внимание уделяется статистическому разнообразию и характеристикам.
Измерение какого-либо показателя требует создания временных рядов. На практике они применяются для описания природных, технических, экономических систем или погодных данных. Примером может стать биржевой курс. Его исследование сводится к изучению трендов или направленности колебаний котировок ценных бумаг.
Временные ряды широко используются для прогнозирования. Они обладают следующими характеристиками:
Они могут демонстрировать полный рост или тенденции в длительном периоде. Ряд может быть полным, но статичным, с тенденциями к последнему периоду, а может быть неполного роста с тенденциями за последний период. Для прогнозирования применяются модели экспоненциального сглаживания, модели скользящего среднего, трендовые модели.
Особенности эконометрических исследований
Эконометрика является частью экономической теории. Она изучает количественные и качественные связи в хозяйственных системах с помощью математических и статистических методов. Эконометрические исследования имеют несколько характеристик:
Готовые работы на аналогичную тему
Самыми распространенными методами эконометрики являются регрессионный анализ, анализ временных рядов, панельный анализ. Эконометрика, как наука, часто подвергается критике, так как не дает четкой связи с конкретными фактами. То есть, считается, что теоретические расчетные данные слишком далеки от реальных событий в хозяйственных системах. Однако, перечисленные методы позволяют формализовать и описать многие процессы, а так же проанализировать их. Например, парный регрессионный анализ способствует поиску статистической выборки, разработке экономической модели, ее построению, оценке качества, созданию графика, формированию выводов. Эконометрические исследования помогают изучить такие явления, как темпы роста инфляции, показатели банкротства предприятия, влияние факторов на уровень спроса, на совокупный объем выпуска, а так же изучить влияние показателей на величину денежной массы.
Панельный анализ направлен на изучение выборок, которые берутся в определенной временной последовательности. Здесь учитывается три измерения – признаки, объекты, время. Анализ позволяет исследовать такие социально-экономические явления, как безработица, преступность, результативность государственной политики.
Временные ряды в эконометрических исследованиях
Временные ряд применяются для анализа последовательности измерений. Чаще всего, они используются для исследования экономических процессов. Элементы ряда измеряются последовательно, обычно через равные временные отрезки. Для удобства данные нумеруют, а так же отмечают время замера. То есть, порядок сбора информации для последующего исследования является существенным.
Анализ временных рядов осуществляется совокупностью математических и статистических методов. Это необходимо для выявления структуры временных рядов, использования их в прогнозировании. Структура необходима для того, чтобы сформировать математическую модель. Анализ временных рядов делает прогностические модели обоснованными, так как он учитывает определенные условия и свойства ряда.
Существенность сбора данных проявляется в том, что временной ряд должен иметь достаточный объем. В нем должно повторяться не менее 4 циклов процессов. Случайные данные ряда не должны быть соизмеримыми с другими компонентами. Только в этом случае полученные результаты исследования будут значимыми для исследователя.
Практическое применение временных рядов актуально для сезонных товаров. С их помощью можно отслеживать тренды, как в примере с колебанием биржевых котировок. Тенденции прогноза так же можно отследить с помощью временных рядов. Они показывают особенности тренда – постоянный, затухающий, экспоненциальный или падение. Для составления прогнозов тенденции могут быть важны как в долгосрочном периоде, так и в последнем временном отрезке.
Результатом исследования становится построение модели. В некоторых случаях применяется экспоненциальное сглаживание, либо сглаживание с трендом или сезонностью. Скользящая средняя так же используется сама по себе, либо с учетом сезонности. Трендовые модели опираются на линейные, логарифмические, экспоненциальные расчеты.
Таким образом, временные ряды являются частью эконометрического инструментария, используемого для исследования хозяйственных структур, событий, явлений, закономерностей. Они помогают увязывать показатели и временные изменения, то есть изучать события в динамике. Особенно это актуально для описания бизнес-процессов, либо тенденций в заданных условиях.
Временные ряды. Простые решения
В этой статье мы рассмотрим несколько простых подходов прогнозирования временных рядов.
Материал, изложенный в статье, на мой взгляд, хорошо дополняет первую неделю курса «Прикладные задачи анализа данных» от МФТИ и Яндекс. На обозначенном курсе можно получить теоретические знания, достаточные для решения задач прогнозирования рядов динамики, а в качестве практического закрепления материала предлагается с помощью модели ARIMA библиотеки scipy сформировать прогноз заработной платы в Российской Федерации на год вперед. В статье, мы также будем формировать прогноз заработной платы, но при этом будем использовать не библиотеку scipy, а библиотеку sklearn. Фишка в том, что в scipy уже предусмотрена модель ARIMA, а sklearn не располагает готовой моделью, поэтому нам придется потрудиться ручками. Таким образом, нам для решения задачи, в каком то смысле, необходимо будет разобраться как устроена модель изнутри. Также, в качестве дополнительного материала, в статье, задача прогнозирования решается с помощью однослойной нейронной сети библиотеки pytorch.
Весь код написан на python 3 в jupyter notebook. Более того, notebook устроен таким образом, что вместо данных о заработной плате можно подставить многие другие ряды динамики, например данные о ценах на сахар, поменять период прогнозирования, валидации и обучения, добавить иные внешние факторы и сформировать соответствующий прогноз. Другими словами, в работе используется простенький самописный тренажерчик, с помощью которого можно прогнозировать различные ряды динамики. Код можно посмотреть здесь
План статьи
Краткое описание тренажера
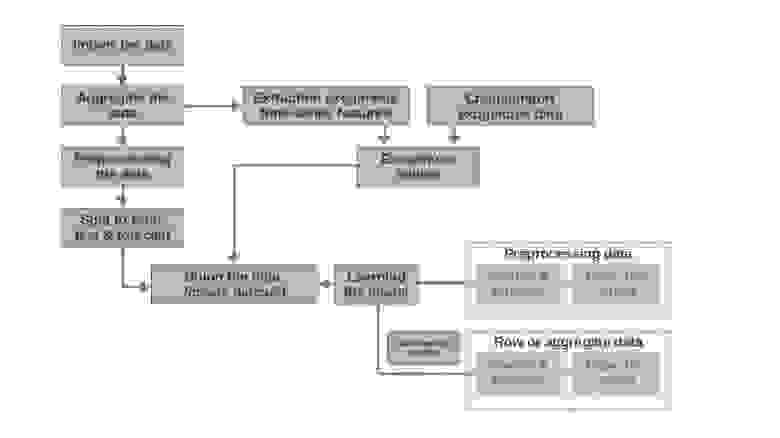
Import the data
Здесь все просто — импортируем данные. Иногда бывает так, что сырых данных достаточно для формирования более-менее внятного прогноза. Именно первый и второй прогнозы в статье моделируются на основании сырых данных, то есть для прогноза заработной платы используются необработанные данные о заработной плате в прошлые периоды.
Aggregate the data
В статье не используется агрегация данных ввиду отсутствия необходимости. Однако зачастую, данные могут быть представлены неравными временными интервалами. В таком случае, просто необходимо их агрегировать. Например, данные с торгов ценными бумагами, валютой и другими финансовыми инструментами необходимо агрегировать. Обычно берут среднее значение в интервале, но можно и максимальное, минимальное, стандартное отклонение и другие статистики.
Preprocessing the data
В нашем случае, речь идет в первую очередь о предобработке данных, благодаря которой, временной ряд приобретает свойство гомоскедастичности (через логарифмирование данных) и становится стационарным (через дифференцирование ряда).
Split to train, test & forecast
В этом блоке кода временные ряды разбиваются на периоды обучения, тестирования и прогнозирования путем добавления нового столбца с соответствующими значениями «train», «test», «forecast». То есть, мы не создаем три отдельных таблицы для каждого периода, а просто добавляем столбец, на основании, которого в дальнейшем будем разделять данные.
Extraction exogenous time-series features
Бывает полезным выделить дополнительные внешние (экзогенные) признаки из временного ряда. Например, указать выходной это день или нет, указать количество дней в месяце (или количество рабочих дней в месяце) и др. Как правило эти признаки «вытаскиваются» из самого временного ряда без какого либо ручного вмешательства.
Create/import exogenous data
Не всю информацию можно «вытащить» из временного ряда. Иногда могут потребоваться дополнительные внешние данные. Например, какие-то эпизодические события, которые оказывают сильное влияние на значения временного ряда. Такими событиями могут быть даты начала военных действий, введения санкций, природные катаклизмы и др. В работе такие факторы не рассматриваются, однако возможность их использования стоит иметь в виду.
Exogenous values
В этом блоке кода мы объединяем все экзогенные данные в одну таблицу.
Union the data (create dataset)
В этом блоке кода мы объединяем значения временного ряда и экзогенных признаков в одну таблицу. Другими словами — готовим датасет, на основании, которого будем обучать модель, тестировать качество и формировать прогноз.
Learning the model
Здесь все понятно — мы просто обучаем модель.
Preprocessing data: predict & forecast
В случае, если мы для обучения модели использовали предобаботанные данные (логарифмированные, обработанные функцией бокса-кокса, стационарный ряд и др.), то качество модели для начала оценивается на предобработанных данных и только потом уже на «сырых» данных. Если, мы данные не предобрабатывали, то данный этап пропускается.
Row data: predict & forecast
Данный этап является заключительным. Если, модель обучалась на предобработанных данных, например, мы их прологарифмировали, то для получения прогноза заработной платы в рублях, а не логарифма рублей, нам следует перевести прогноз обратно в рубли.
Также хотелось бы отметить, что в статье используется одномерный временной ряд для предсказания заработной платы. Однако ничего не мешает использовать многомерный ряд, например добавить данные курса рубля к доллару или какой-либо другой ряд.
Решение в лоб
Будем считать, что данные о заработной плате в прошлом, могут аппроксимировать заработную плату в будущем. Иначе можно сказать — размер заработной платы, например, в январе зависит от того, какая заработная плата была в декабре, ноябре, октябре,…
Давайте возьмем значения заработной платы в 12-ть прошлых месяцев для предсказания заработной платы в 13-й месяц. Другими словами для каждого целевого значения у нас будет 12 признаков.
Признаки будем подавать на вход Ridge Regression библиотеки sklearn. Параметры модели берем по умолчанию за исключением параметра alpha, его установили на 0, то есть по сути мы используем обычную регрессию.
Это и есть решение в лоб — оно самое простое:) Бывают ситуации, когда нужно очень срочно дать хоть какой-то результат, а времени на какую-либо предобработку просто нет или не хватает опыта, чтобы оперативно обработать или добавить данные. Вот в таких ситуациях, можно в качестве baseline использовать сырые данные для построения прогноза. Забегая вперед, отмечу, что качество модели оказалось сопоставимо с качеством моделей, в которых используется предобработка данных.
Давайте посмотрим, что у нас получилось.
На первый взгляд результат выглядит хоть и неидеально, но близко к действительности.
В соответствии со значениями коэффициентов регрессии, наибольшее влияние на прогноз заработной платы оказывает значение заработной платы ровно год назад.
Попробуем добавить в модель экзогенные переменные.
Добавление экзогенных переменных
Мы будем использовать 2 внешних признака: количество дней в месяце и номер месяца (от 1 до 12). Признак «Номер месяца» мы бинаризируем, в итоге у нас получится 12 столбцов для каждого месяца со значениями 0 или 1.
Сформируем новый датасет и посмотрим на качество модели.
Качество получилось ниже. Визуально заметно, что прогноз выглядит не совсем правдоподобно в части роста заработной платы в декабре.
Давайте теперь проведем первую предобработку данных.
Коррекция гетероскедастичности.
Если мы посмотрим на график заработной платы за период с 2010 по 2020 гг, то мы увидим, что ежегодно разброс заработной платы внутри года между месяцами растет.
Ежегодный рост дисперсии от месяца к месяцу приводит к гетероскедастичности. Для улучшения качества прогнозирования нам следует избавиться от этого свойства данных и привести их к гомоскедастичности.
Для этого воспользуемся обычным логарифмированием и посмотрим как выглядит прологарифмированный ряд.
Обучим модель на прологарифмированном ряду
В итоге качество предсказаний на обучающей и тестовой выборках действительно улучшилось, однако прогноз на 2021 год по сравнению с прогнозом первой модели визуально выглядит менее правдоподобным. Скорее всего использование экзогенных факторов ухудшает модель.
Приведение ряда к стационарному
Приводить ряд к стационарному будем следующим образом:
Ряд действительно выглядит стационарным, об этом также говорит значение критерия Дики-Фуллера.
Ожидать хорошее качество предсказаний на обучающей и тестовой выборках на обработанных данных, то есть на стационарном ряду не приходится, так как по сути, в этом случае модель должна предсказывать значения белого шума. Но нам, для прогнозирования заработной платы, уже совсем не обязательно использовать регрессию, так как, приводя ряд к стационарному, мы по-простому говоря, определили формулу аппроксимации целевой переменной. Но мы не будем отходить от канонов и воспользуемся регрессионной моделью, к тому же у нас есть экзогенные факторы.
Давайте посмотрим, что получилось.
Вот так выглядит предсказание стационарного ряда. Как и ожидали — не очень-то и хорошо 🙂
А вот предсказание и прогноз заработной платы.
Качество заметно улучшилось и прогноз визуально стал выглядеть правдоподобным.
Теперь сформируем прогноз без использования экзогенных переменных
Качество еще улучшилось и правдоподобность прогноза сохранилась 🙂
Прогнозирование с помощью однослойной нейронной сети
На вход нейронной сети будем подавать имеющиеся датасеты. Так как наша сеть однослойная, то по сути это и есть та же самая линейная регрессия с незамысловатыми модификациями и ожидать сильно большую разницу в качестве предсказаний не стоит.
Для начала посмотрим на саму сеть
Теперь пару слов о том, как будем ее обучать.
Не будем рассматривать качество предсказаний для каждого датасета отдельно (желающие могут посмотреть подробности на гите). Давайте сравним итоговые результаты.
Качество на тестовой выборке с использованием Ridge Regression
Качество на тестовой выборке с использованием Single layer NN
Как мы и ожидали, принципиальной разницы между обычной регрессией и простой однослойной нейронной сетью не оказалось. Конечно, нейронки дают больше маневра для обучения: можно менять оптимизаторы, регулировать шаги обучения, использовать скрытые слои и функции активации, можно пойти еще дальше и использовать рекуррентные нейронные сети — RNN. К слову, лично мне не удалось получить вменяемого качества в данной задаче с использованием RNN, однако на просторах интернета можно встретить много интересных примеров прогнозирования временных рядов с использованием LSTM.
На этом моменте статья подошла к завершению. Надеюсь, материал будет полезен как некий обзор baseline-подходов, применяемых при прогнозировании временных рядов и послужит хорошим практическим дополнением к курсу «Прикладные задачи анализа данных» от МФТИ и Яндекс.
Временной ряд
Временной ряд — это упорядоченная последовательность значений какого-либо показателя за несколько периодов времени. Основная характеристика, которая отличает временной ряд от простой выборки данных, — указанное время измерения или номер изменения по порядку.
Пример временного ряда: биржевой курс.
Пример выборки данных: электронные почты клиентов магазина.
Где применяются временные ряды
Временные ряды используются для аналитики и прогнозирования, когда важно определить, что будет происходить с показателями в ближайший час/день/месяц/год: например, сколько пользователей скачают за день мобильное приложение. Показатели для составления временных рядов могут быть не только техническими, но и экономическими, социальными и даже природными.
Прогнозирование временных рядов
Модели ARMA и ARIMA
Они сыграли фундаментальную роль в обработке сигналов связи во время Второй мировой войны. После их начали использовать в анализе временных рядов в 1970 году.
ARMA (Autoregressive Moving Average) — авторегрессионная модель скользящей средней.
ARIMA (Autoregressive Integrated Moving Average) — авторегрессионная интегрированная модель скользящей средней.
AR → Авторегрессионная модель
В ней значения в будущем определяются как значения из прошлого, умноженные на коэффициенты.
Это относится к различным методам вычисления различий между последовательными наблюдениями для получения стационарного процесса из нестационарного.
MA → Модель скользящей средней
Это регрессионная модель, которая использует прошлые ошибки прогноза для прогнозирования интересующей переменной.
Для работы с временными рядами с сезонными компонентами используется SARIMA (интегрированное скользящее среднее сезонной авторегрессии). Это расширение модели ARIMA, добавляющее в нее сезонные условия.
Data Scientist с нуля
Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.
Prophet
Prophet разработан командой Facebook Core Data Science и представляет собой инструмент с открытым исходным кодом для бизнес-прогнозирования. Модель Prophet основана на трех переменных:
g (t) — тренд. Логистическая функция позволяет моделировать рост с насыщением, когда при увеличении показателя снижается темп его роста.
s (t) — сезонность отвечает за моделирование периодических изменений, связанных с недельной и годовой сезонностью.
h (t) — праздники и события. Учитываются аномальные дни, которые не влияют на сезонность.
ε(t) — ошибка. Содержит информацию, которую модель не учитывает.
У Prophet существует больше инструментов для обработки и сортировки данных по сезонности, чем у SARIMA. Такое преимущество позволяет анализировать временные ряды с различной сезонностью — неделей, месяцем, кварталом или годом.
Прогноз по методу экспоненциального сглаживания
Преимущество этого метода — возможность сделать прогноз на длительный период. Математически экспоненциальное сглаживание выражается так:
a (alfa) — коэффициент сглаживания, который принимает значения от 0 до 1. Он определяет, насколько продолжительность изменит существующие значения в базе данных.
x — текущее значение временного ряда (например, объем продаж).
y — сглаженная величина на текущий период.
t — значение тренда за предыдущий период.
Пример экспоненциального сглаживания:
Голубая линия на графике — это исходные данные, темно-синяя линия представляет экспоненциальное сглаживание временного ряда с коэффициентом сглаживания 0,3, а оранжевая линия использует коэффициент сглаживания 0,05. Чем меньше коэффициент сглаживания, тем более плавным будет временной ряд.
Временные ряды и их характеристики
Предполагается, что временные ряды генерируются регулярно, но на практике это не всегда так. В нерегулярных рядах измерения нельзя провести через одинаковые промежутки времени. Примером нерегулярного временного ряда является пополнение банковской карты.
Типы временных рядов
Помимо регулярности, временные ряды делятся на детерминированные и недетерминированные.
Детерминированный временной ряд — ряд, в котором нет случайных аспектов или показателей: он может быть выражен формулой. Это значит, что мы можем проанализировать, как показатели вели себя в прошлом, и точно прогнозировать их поведение в будущем.
Недетерминированный временной ряд имеет случайный аспект и прогнозирование будущих действий становится сложнее. Природа таких показателей случайна.
Стационарные и нестационарные ряды
На наблюдение за показателями и их систематизацией влияют тенденции и сезонные эффекты. От этих условий зависит сложность моделирования системы прогнозирования. Временные ряды можно разделить по наличию или отсутствию тенденций и сезонных эффектов на стационарные и нестационарные.
В стационарных временных рядах статистические свойства не зависят от времени, поэтому результат легко предсказать. Большинство статистических методов предполагают, что все временные ряды должны быть стационарными. Пример стационарных временных рядов — рождаемость в России. Конечно, она зависит от множества факторов, но ее спад или рост возможно предсказать: у рождаемости нет ярко выраженной сезонности.
В нестационарных временных рядах статистические свойства меняются со временем. Они показывают сезонные эффекты, тренды и другие структуры, которые зависят от временного показателя. Пример — международные перелеты авиакомпаний. Количество пассажиров на тех или иных направлениях меняется в зависимости от сезонности.
Для классических статистических методов удобнее создавать модели стационарных временных рядов. Если прослеживается четкая тенденция или сезонность во временных рядах, то следует смоделировать эти компоненты и удалить их из наблюдений.
Прогнозирование временных рядов — популярная аналитическая задача, которую используют в разных сферах жизни — бизнесе, науке, исследованиях общества и потребительского поведения. Прогнозы используются для предсказания, например, сколько серверов понадобится онлайн-магазину, когда спрос на товар вырастет.
Освойте необходимые навыки и инструменты и пройдите через все этапы работы над аналитическим проектом. Дополнительная скидка 5% по промокоду BLOG.










