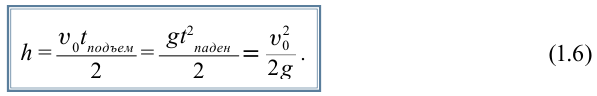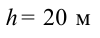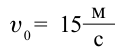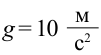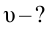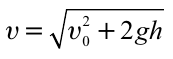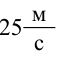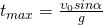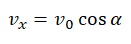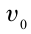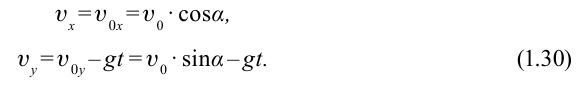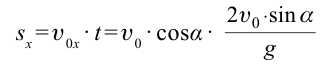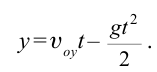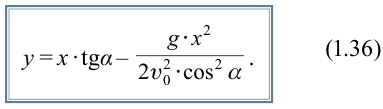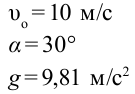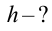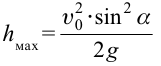Что такое время подъема
Вертикальное движение тел:
Если держать в руках какой-либо предмет, а затем отпустить его, то предмет из-за притяжения Земли начнет двигаться прямо к ее поверхности. Такое движение тел называется вертикальное движение вниз. С этим движением вы ознакомились на уроках физики в 7 классе. В этой теме мы рассмотрим вертикальное движение вниз с точки зрения принципа независимости движений.
Когда тело двигается вертикально, на него действует одна или несколько сил (сила тяжести, сила сопротивления воздуха, сила Архимеда). В случае движения тел вверх (вертикально) в целях упрощения задачи мы не учитываем силу сопротивления воздуха и силу Архимеда.
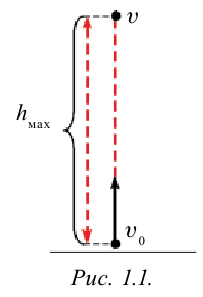
Понаблюдаем за движением какого-либо предмета, подбросив его вверх в вертикальном направлении (рис. 1.1.). Если бы тело двигалось вверх только со скоростью
Движение тела, брошенного вертикально вверх, является равнозамедленным движением.
Скорость тела через время 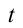
Тело останавливается при достижении самой верхней точки 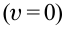
Приравнивая левую сторону выражения (1.4) нулю, находим выражение для определения времени, необходимого для подъема тела:
Максимальная высота подъема тела определяется выражением:
В условиях, когда сопротивление воздуха ничтожно мало и можно его не учитывать, время подъема брошенного вверх тела будет равно времени падения вниз 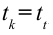
Тело, брошенное вертикально вниз, совершает равномерно ускоренное движение. Здесь скорость тела через время 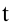
Уравнение движения тела, брошенного вертикально вниз, запишем следующим образом:
Первым закономерности вертикального движения тел экспериментальным способом начал изучать великий итальянский ученый Г. Галилей. На основе проведенных опытов были обнаружены две закономерности вертикального падения тел. Во-первых, вертикальное падение тела является прямолинейным равноускоренным движением, во-вторых, все тела при свободном падении двигаются с постоянным ускорением.
Если учесть, что свободное падение тел является равноускоренным движением, то все уравнения прямолинейного равноускоренного движения в этом случае также действительны, т.е. можно заменить ускорение 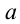
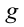
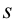
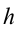
Из-за того, что свободное падение происходит равноускоренно, а движение вертикально вверх – равнозамедленно, среднюю скорость движения тела можно определить из следующего выражения:
Образец решения задачи:
Начальная скорость предмета, падающего с крыши здания высотой
20 м, равна 15 м/сек. Чему равняется его скорость в момент столкновения
с землей?
Решение: 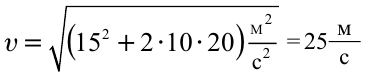
Ответ:
| Уравнения равноускоренного движения | Уравнения движения при свободном падении |
|---|---|
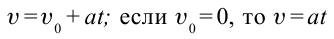 | 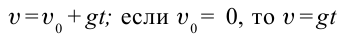 |
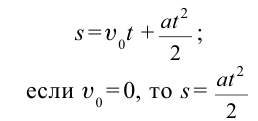 | 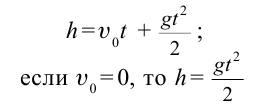 |
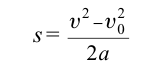 | 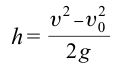 |
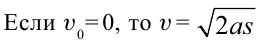 | 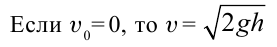 |
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как сказал.
Стремись не к тому, чтобы добиться успеха, а к тому, чтобы твоя жизнь имела смысл.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Время подъема на максимальную высоту, тела, брошенного под углом к горизонту
Движение тела, брошенного под углом к горизонту:
v0 — начальная скорость тела, брошенного под углом к горизонту
v0х — проекция начальной скорости на ось x
v0y — проекция начальной скорости на ось y
a — угол под которым было брошено тело
t — время тела в полете
g — ускорение свободного падения
Законы и формулы
Сейчас 109 гостей и ни одного зарегистрированного пользователя на сайте
Спасибо тем авторам и правообладателям, которые согласны на размещение своих материалов на моем сайте! Вы вносите неоценимый вклад в обучение, воспитание и развитие подрастающего поколения.
Движение тела, брошенного под углом к горизонту (бросок)
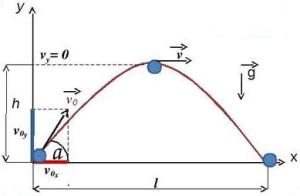
Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом к оси ОХ (рис. 1).
Рис. 1. Тело бросили под углом к горизонту
Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).
Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)
Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( (м/ ), а на ось OY ( (м/ ).
Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.
Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)
Вернёмся к рисунку 2. Попробуем найти полное время полёта ( ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:
— т.к. время движения от точки А до B, и от B до C одинаково. Тогда:
Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( ).
Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время :
Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.
Рис. 4. Тело бросили под углом к горизонту (конечная скорость)
Используя (5), получим:
Подставим (12) и (13) в (10):
Вывод:
Движение тела, брошенного под углом к горизонту
теория по физике 🧲 кинематика
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты! График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
Уравнение координаты x:
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Алгоритм решения
Решение
Запишем исходные данные:
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Потенциальная энергия шарика в точке А равна:
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
Перед ударом кинетическая энергия шарика равна:
Согласно закону сохранения энергии:
E p A = E p B + E k B
Отсюда высота H равна:
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
pазбирался: Алиса Никитина | обсудить разбор | оценить
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение тела, брошенного под углом к горизонту:
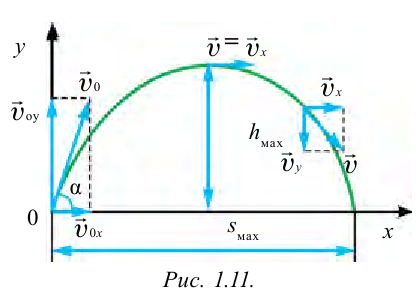
Если рассмотреть движение тела, брошенного под углом относительно горизонта, можно увидеть, что тело отдаляется горизонтально от точки броска и одновременно поднимается в вертикальном направлении. Значит, тело, брошенное под углом к горизонту, участвует в двух (горизонтальном и вертикальном) видах движения. В горизонтальном направлении тело движется равномерно. В вертикальном направлении до точки максимальной высоты тело будет двигаться равнозамедленно, затем вниз будет двигаться равноускоренно (рис. 1.11).
Траектория движения тела, брошенного под углом к горизонту, имеет вид параболы. Учитывая, что в процессе полета тело одновременно двигается в горизонтальном и вертикальном направлениях, разделим начальную скорость
Для упрощения расчетов пренебрежем сопротивлением воздуха. В произвольный момент времени 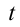
В произвольный момент времени t скорость тела в горизонтальном и вертикальном направлениях можно найти из следующих уравнений:
На протяжении движения тела, брошенного под углом к горизонту, горизонтальная составляющая скорости не меняется, вертикальная составляющая при подъеме является равнозамедленной и на максимальной высоте подъема равняется нулю. Значит, тело, брошенное под углом к горизонту, имеет минимальную скорость в высшей точке траектории:
Затем из этой точки тело движется как тело, брошенное горизонтально со скоростью 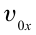
Из соотношения 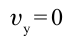
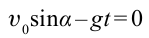
Максимальная высота подъема тела определяется следующим соотношением:
Время движения тела вниз (падение) равно времени подъема, т.е. 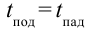
Тело, брошенное под углом к горизонту, в горизонтальном направлении движется равномерно. По этой причине длина полета тела зависит только от горизонтальной составляющей скорости. Для определения дальности полета подставим выражение 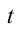
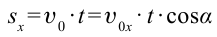
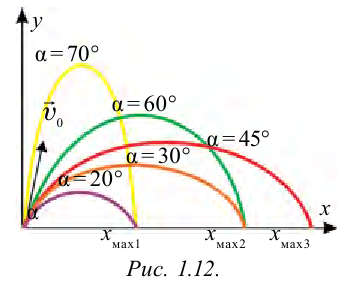
Из этого выражения видно, что длина полета тела, брошенного под углом к горизонту, зависит от угла броска. На рис. 1.12 приведена зависимость длины полета и высоты подъема от угла броска. Из рисунка видно, что с увеличением угла броска увеличивается высота подъема.
подставляем выражение для времени полета 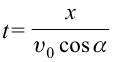
Образец решения задачи:
Мяч брошен со скоростью 10 м/с под углом 30° к горизонту. На какую высоту поднимется мяч?
Дано:
Решение: 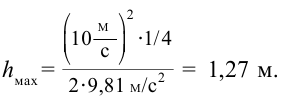
Ответ: 1,27 м.
Основные понятия, правила и законы
| Научное наблюдение | Метод научного исследования системный, активный, направленный на цель. |
| Гипотеза | Предположение о каком-либо процессе, явлении. |
| Опыт (эксперимент) | Проводится для проверки гипотезы в специальных условиях. |
| Модель | Упрощенная версия физического процесса, сохраняющая его главные черты. |
| Научная идеализация | Предсказание получаемого результата в идеальных условиях по ранее полученным результатам. |
| Научная теория | Набор законов, объясняющий широкую область явлений. |
| Принцип соответствия | В определенных рамках соответствие новой и старой теорий. |
| Криволинейное равномерное движение | Движение, траектория которого представляет собой кривую линию, величина скорости не меняется, а направление изменяется по касательной к траектории. |
| Принцип независимости или суперпозиция движения | Движения, в которых участвует тело, независимы друг от друга, и скорости (ускорение) их движения не зависят друг от друга. |
| Вертикальное движение вверх | Движение, противоположное силе притяжения Земли. Уравнение движения: 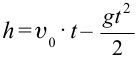 . . |
| Вертикальное движение вниз | Движение в направлении силы притяжения Земли. Уравнение движения: 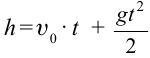 . . |
| Переменное вращательное движение | Вращательное движение, при котором с течением времени меняется угловая скорость. |
| Угловое ускорение | Величина, определяемая отношением изменения угловой скорости ко времени этого изменения 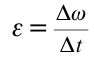 |
| Формула определения угловой скорости в произвольный момент времени при вращательном равнопеременном движении | 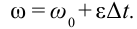 |
| Тангенциальное ускорение | Ускорение, получаемое в связи с изменением величины скорости 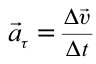 . . |
| Полное ускорение при криволинейном движении | 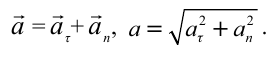 |
| Передача движения фрикционным способом | Движение, передаваемое с помощью действующих поверхностей двух колес с разными радиусами. |
| Ременная передача движения | Движение передается от одного колеса к другому через туго натянутый ремень. |
| Передача движения через зубчатые колеса | Передача вращательного движения путем объединения двух зубчатых колес с разными диаметрами. |
| Дальность полета и скорость при падении горизонтально брошенного тела. | 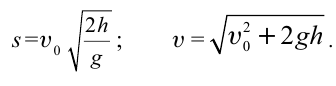 |
| Минимальная скорость тела, брошенного под углом к горизонту | 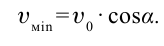 |
| Высота подъема тела, брошенного под углом к горизонту | 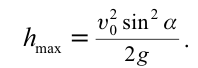 |
| Время полета тела, брошенного под углом к горизонту | 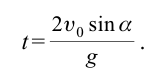 |
| Дальность полета тела, брошенного под углом к горизонту | 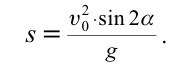 |
| Уравнение траектории движения тела, брошенного горизонтально | 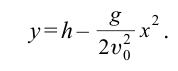 |
| Уравнение траектории движения тела, брошенного под углом к горизонту | 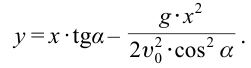 |
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.