Что такое все возможные обозначения полученной прямой
Прямая линия. Понятие прямой, ее свойства.
Наглядно прямую линию может продемонстрировать туго натянутый шнур, кромка стола, край листа бумаги, место, соединения двух стен комнаты, луч света. При начертании прямых линий на практике применяют линейку.
Прямой линии присущи такие характерные особенности:
1.У прямой линии нет ни начала ни конца, то есть она бесконечна. Существует возможность начертить только ее часть.
2.Через две произвольные точки можно провести прямую линию, и притом только одну.
3. Через произвольную точку можно провести не ограниченное количество прямых на плоскости.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны.
Для обозначения прямой линии используют или одну малую букву латинского алфавита, или две большие буквы, написанные в двух различных местах этой прямой.
Если на прямой линии указать точку, то в результате получим два луча:
Лучом называют часть прямой линии, ограниченную с одной стороны. Для обозначения луча применяют или одну малую букву латинского алфавита, или две большие буквы, из которых одна обозначается в начале луча.
Часть прямой, ограниченная с обеих сторон, именуют ее отрезком. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Линию, сформированную несколькими отрезками, не лежащими на одной прямой, принято называть ломаной. Когда концы ломаной совпадают, то такая ломаная именуется замкнутой.
Плоскость, прямая линия, луч
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Обозначение прямой
Например, на рисунке 1 обозначены такие прямые:
Рис. 1 Обозначение прямой линии
Рис. 2 Обозначение прямой с несколькими точками
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
Рис. 5 Пересечение прямых
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
Луч имеет второе название – полупрямая.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.6 / 5. Количество оценок: 22
Прямая линия
Прямая линия — это линия, не имеющая неровностей, скруглений и углов. Прямая линия бесконечна, она не имеет ни начала, ни конца. В геометрии прямая линия называется просто прямой.
Для изображения прямой на бумаге используется линейка. Чтобы начертить прямую, надо провести черту вдоль края линейки:
Так как прямая бесконечна, то какой бы длины не была проведена черта, она будет изображать только часть прямой.
Обозначение прямой
Прямая обозначается одной маленькой латинской буквой, например прямая a, или двумя большими латинскими буквами, поставленными при любых двух точках, лежащих на этой прямой, например прямая AB:
Обратите внимание, что точки на прямой можно обозначать короткими чёрточками.
Свойства прямой
1. Через любые две точки можно провести только одну прямую линию.
Это основное свойство прямой. Оно часто используется на практике, для прокладывания прямых линий с помощью двух каких-либо объектов.
2. Если две любые точки прямой лежат на плоскости, то все точки этой прямой лежат на той же плоскости.
3. Через одну точку можно провести бесконечно много прямых.
4. Есть точки лежащие на прямой и не лежащие на ней.
Точки N и M лежат на прямой a. Точка L не лежит на прямой a.
5. Из трёх разных точек, лежащих на одной прямой, только одна может лежать между двумя другими точками.
На рисунке изображена прямая с тремя точками A, B и C, лежащими на ней. Про эти точки можно сказать:
точка B лежит между точками A и C, точка B разделяет точки A и C
Также можно сказать:
точки B и C лежат по одну сторону от точки A, они не разделяются точкой A
6. Две прямые, лежащие на одной плоскости, или пересекаются друг с другом в одной точке, или являются параллельными.
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Уравнение прямой, виды уравнения прямой на плоскости
В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.
Определение уравнения прямой на плоскости
Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.
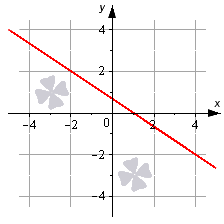
Общее уравнение прямой линии
Поясним некоторые важные аспекты темы.
Посмотрите на рисунок.
Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.
Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.
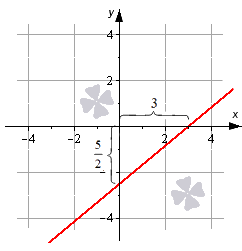
Уравнение прямой в отрезках
Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».
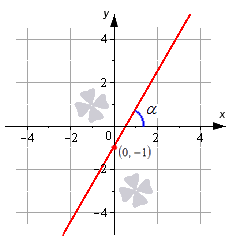
Уравнение прямой с угловым коэффициентом
Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.
Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.
Каноническое уравнение прямой на плоскости
Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.
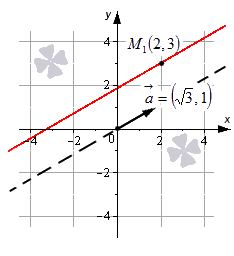
Параметрические уравнения прямой на плоскости
Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.
Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».
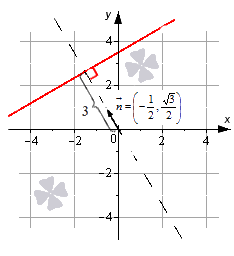
Нормальное уравнение прямой
Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.