Что такое вспомогательный алгоритм в информатике

Информатика. 10 класс (Повышенный уровень)

§ 7. Понятие вспомогательного алгоритма

7.1. Вспомогательные алгоритмы

Вспомогательный алгоритм — алгоритм, который можно использовать в других алгоритмах, указав его имя и, если необходимо, значения параметров. Вспомогательный алгоритм, записанный на языке программирования, называют подпрограммой.

Основные преимущества использования подпрограмм:

1. Разбиение комплексной программной задачи на простые шаги (декомпозиция). Это позволяет распределить решение одной задачи между различными людьми.
2. Уменьшение повторяющегося кода.
3. Многократное использование кода в других программах, в том числе и другими программистами.
4. Сокрытие деталей реализации от пользователей подпрограммы.

Перед тем как использовать функцию, ее нужно описать. Описание функции включает объявление и определение функции.

Объявление функции (пример 7.1) включает в себя заголовок функции, заканчивающийся точкой с запятой и включающий:

Функции могут быть с параметрами или без параметров. Если функция не имеет параметров, то наличие круглых скобок после имени функции обязательно.

Определение функции состоит из заголовка функции (без точки с запятой) и тела функции, заключенного в фигурные скобки. В нем содержатся команды языка, реализующие вспомогательный алгоритм (пример 7.2).

При вызове функции (пример 7.3) указывается ее имя и параметры, необходимые для вычислений. Эти параметры называют фактическими параметрами.

В описании функции задается список формальных параметров. Каждый параметр, описанный в этом списке, является локальным по отношению к описываемой функции, т. е. на него можно ссылаться по его имени из данной подпрограммы, но не из основной программы или другой функции.

Переменные, значения которых должны быть известны во всех функциях, являются глобальными и описываются до описания функций. Если переменная описана между описаниями функций, то ее значение будет глобальным для всех функций, описанных ниже, но неизвестным для функций, описанных выше.

Необходимость оптимизации программ по объему занимаемой памяти привела к появлению подпрограмм. Подпрограммы позволили не повторять в программе идентичные блоки кода, а описывать их однократно и вызывать по мере необходимости.

Использование подпрограмм позволяет повысить надежность кода программы. Подпрограммы обычно имеют небольшой размер, поэтому найти и исправить в них ошибки проще, нежели в большой программе.

Использование подпрограмм гарантирует относительную автономность модификации программы: если нужно что-либо изменить в программе, переделывать придется не всю программу, а только некоторые подпрограммы.

Пример 7.1. Объявление функций.

int kol _ cifr ( int n );
double plos_treug ( double a, double h );

Источник

Что такое вспомогательный алгоритм в информатике

§ 13. Понятие вспомогательного алгоритма

Представьте себе, что вы находитесь в летнем лагере труда и отдыха, вас назначили дежурным по столовой и вы хотите продумать порядок своих действий. Ясно, что некоторые обязанности дежурного придется в течение дня исполнять несколько раз. Например, такие:

Эту последовательность действий предстоит выполнить три раза за дежурство: после завтрака, обеда и ужина. Назовем соответствующий алгоритм «Обязанности», а при написании распорядка дня заменим эти четыре действия одной командой:

Тогда распорядок дежурства по столовой примет такой вид:

Легко понять, что использование команды «Выполнить алгоритм. » позволило почти в два раза сократить длину нашей инструкции.

Подобным образом поступают часто, когда при составлении алгоритма возникает необходимость многократного использования одного и того же набора действий.

указывая вместо многоточия имя алгоритма. Такие команды называются командами вызова вспомогательного алгоритма.

Составляя для исполнителя вспомогательные алгоритмы, мы как бы «обучаем» исполнителя новым действиям. Точно так же происходит и обучение в школе. Вначале школьников обучают сложению и вычитанию, затем, используя эти умения, обучают действиям умножения и деления, которые, в свою очередь, используются в дальнейшем при решении более сложных задач.

Дадим алгоритму решения квадратных уравнений имя «РЕКВУР» (впрочем, вы можете назвать этот алгоритм по-другому, более благозвучно).

И в X классе вы, конечно, сталкивались с квадратными уравнениями в ходе решения различных задач. Но теперь решение квадратных уравнений стало для вас столь же элементарным, как перемножение чисел (возможно, что мы выдаем желаемое за действительное). Можно сказать, что «РЕКВУР» стал вашим вспомогательным алгоритмом.

Давайте проанализируем, как мы выполняем алгоритм «РЕКВУР». Скажем, нужно решить уравнение

Мы вспоминаем «РЕКВУР», подставляем вместо а, b, с числа 2, 3 и 122 и получаем результат: x₁ и х₂. Чтобы решить другое квадратное уравнение, надо подставить вместо а, b, с другие числа.

Записывая вспомогательный алгоритм, естественно указывать, кроме названия, аргументы и результат. Например, запись вспомогательного алгоритма «РЕКВУР» можно начать так:

При вызове вспомогательного алгоритма надо указывать значения исходных данных. Например, вызов вспомогательного алгоритма «РЕКВУР» можно записать так:

(вместо многоточий надо писать конкретные числа или выражения).

Давайте с помощью алгоритма «РЕКВУР» решим какую-нибудь задачу из вашего учебника «Алгебра и начала анализа». Заглянем в него. Вот, например, тема «Показательные уравнения и неравенства». В ней объясняется, как решать уравнения вида

По сути дела, в вашем учебнике предлагается следующий алгоритм решения таких уравнений:

Понятно, что надо как-то различать переменные, одинаково обозначенные в основном и вспомогательном алгоритмах. Поэтому договариваются считать, что все обозначения из вспомогательного алгоритма действительны только в пределах этого алгоритма. Сказанное, конечно же, не относится к результатам работы вспомогательного алгоритма, потому что они должны использоваться и после завершения его работы.

Образно говоря, переменные, имеющие одно и то же название в основном и вспомогательном алгоритмах,- просто «однофамильцы». При вызове вспомогательного алгоритма значения переменных основного алгоритма как бы «замораживаются», а после окончания работы вспомогательного алгоритма они «размораживаются».

Без такого «замораживания» то и дело происходили бы пренеприятнейшие вещи. Какие? Сейчас увидите!

Попробуем решить уравнение

«Замораживание» переменных надежно предохраняет их от порчи вспомогательными алгоритмами

Результат верного алгоритма

Вопросы

1. Что такое вспомогательный алгоритм?

2. Как сделать алгоритм вспомогательным?

3. Как записывается команда вызова вспомогательного алгоритма?

4. В чем заключается «замораживание» и «размораживание» переменных при использовании вспомогательного алгоритма?

Задания для самостоятельного выполнения

1. Какие вспомогательные алгоритмы можно выделить в распорядке дня в школе?

2. Имеется следующий вспомогательный алгоритм:

Записать команды вызова этого вспомогательного алгоритма, выполнив которые исполнитель (человек):

Источник

Урок 26
§34. Вспомогательные алгоритмы

Содержание урока

Что такое вспомогательный алгоритм?

Что такое вспомогательный алгоритм?

Ключевые слова:

В этой задаче Роботу нужно закрасить по три клетки в двух совершенно одинаковых помещениях, имеющих форму сапога (рис. 6.16).

Конечно, было бы хорошо, если бы у Робота была команда (например, Сапог), выполняя которую, Робот обрабатывает такое помещение и возвращается обратно. Тогда бы мы написали такую программу:

алг Два сапога

вправо; вправо; вправо

Для сокращения длины программы мы записали несколько команд в одной строке, разделив их точкой с запятой.

Обсудите в классе, какая ошибка возникнет, если запустить эту программу. Почему?

Но в системе команд Робота нет команды Сапог! Однако всё можно исправить, если объяснить Роботу, что ему нужно делать по команде Сапог. Для этого достаточно записать в конце программы (после служебного слова кон) вспомогательный алгоритм:

алг Сапог

Теперь программа запускается и работает.

Вспомогательный алгоритм решает отдельную задачу и может быть использован при решении более сложных задач. Вызов вспомогательного алгоритма можно использовать так же, как команды из СКИ исполнителя.

Вспомогательный алгоритм часто называют процедурой.

Давайте разберёмся, что будет происходить при запуске этой программы. Алгоритм, записанный в самом начале программы (у нас это алгоритм Два сапога), называется основной программой. Компьютер выполняет основную программу. В первой же строке он встречает неизвестную команду Сапог, которая не входит в СКИ исполнителя Робот. Значит, это вызов вспомогательного алгоритма (процедуры).

Для того чтобы вызвать вспомогательный алгоритм (процедуру), нужно записать его название в теле другого алгоритма.

Если в основной программе нет вызова процедуры, эта процедура не выполнится ни разу, хотя и будет записана в тексте программы.

Вспомогательный алгоритм выполняется только тогда, когда он вызван.

Встретив вызов процедуры Сапог, компьютер ищет процедуру с таким названием ниже основной программы. Если она найдена, то выполняются все команды, записанные в теле этого вспомогательного алгоритма. Затем происходит возврат из процедуры — передача управления на ту команду в основной программе, которая записана сразу после команды Сапог.

После завершения работы процедуры управление передаётся обратно, к следующей команде вызывающей программы.

Для того чтобы увидеть, как передаётся управление, в КуМире можно использовать пошаговый режим с входом в процедуры (клавиша F7).

Конечно, эту задачу можно было бы решить и без процедуры, но решение с процедурой получилось короче. Нам не пришлось писать два раза одинаковые команды. Кроме того, если в какой- то совершенно другой задаче Роботу нужно будет закрашивать клетки в таком же помещении, мы сможем использовать готовый вспомогательный алгоритм Сапог.

Следующая страница Два метода составления программ

Cкачать материалы урока

Источник

§ 23. Вспомогательные алгоритмы и подпрограммы

Еще одним важнейшим методологическим приемом структурного программирования является декомпозиция решаемой задачи на подзадачи — более простые, с точки зрения программирования, части исходной задачи. Алгоритмы решения таких подзадач называются вспомогательными алгоритмами.

Идея решения состоит в следующем математическом факте: если х, у, z — три натуральных числа, то НОД(x, у, z) = = НОД(НОД(х, у), z). Иначе говоря, нужно найти НОД двух величин, а затем НОД полученного значения и третьего числа (попробуйте это доказать).

Очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения наибольшего общего делителя двух чисел. Эта задача решается с помощью алгоритма Евклида, который подробно обсуждался в 9 классе. Напомним, что идея алгоритма Евклида основана на следующей формуле:

Приведем алгоритм решения поставленной задачи на учебном Алгоритмическом языке. Алгоритм состоит из процедуры «Евклид» и основного алгоритма «Задача», в котором присутствуют два обращения к процедуре:

Здесь М, N и К являются формальными параметрами процедуры. М и N — параметры-аргументы, К — параметр-результат.

Процедуры в Паскале. Основное отличие процедур в Паскале от процедур в Алгоритмическом языке (АЯ) состоит в том, что процедуры в Паскале описываются в разделе описания подпрограмм, а в АЯ процедура является внешней по отношению к вызывающей программе. Теперь посмотрим, как решение поставленной задачи программируется на Паскале.

В данном примере обмен аргументами и результатами между основной программой и процедурой производится через параметры. Описание процедуры на Паскале имеет следующий формат:

Квадратные скобки указывают на то, что список формальных параметров может отсутствовать, т. е. возможна процедура без параметров. Параметры могут быть параметрами-переменными и параметрами-значениями. Параметры-переменные записываются следующим образом:

Параметры-значения указываются так:

Чаще всего аргументы представляются как параметры-значения (хотя могут быть и параметрами-переменными). А для передачи результатов используются параметры-переменные. Процедура в качестве результата может передавать в вызывающую программу множество значений (в частном случае — одно), а может и ни одного. Теперь рассмотрим правила обращения к процедуре. Обращение к процедуре производится в форме оператора процедуры:

Если описана процедура с формальными параметрами, то обращение к ней производится оператором процедуры с фактическими параметрами. Правила соответствия между формальными и фактическими параметрами: соответствие по количеству, соответствие по последовательности и соответствие по типам.

Взаимодействие формальных и фактических параметров через параметры-переменные называется передачей по ссылке: при обращении к процедуре ей передается ссылка на переменную, заданную в качестве фактического параметра. Эта ссылка и используется процедурой для доступа к этой переменной.

Другой вариант взаимодействия формальных и фактических параметров называется передачей по значению: вычисляется значение фактического параметра (выражения), и это значение присваивается соответствующему формальному параметру.

Теперь рассмотрим другой вариант программы, решающей ту же задачу. В ней используется процедура без параметров.

Чтобы разобраться в этом примере, требуется объяснить новое для нас понятие: область действия описания.

Областью действия описания любого программного объекта (переменной, типа, константы и т. д.) является тот блок, на который это описание распространяется. Если данный блок вложен в другой (подпрограмма), то присутствующие во вложенном блоке описания являются локальными. Они действуют только в пределах внутреннего блока. Описания же, расположенные во внешнем блоке, называются глобальными по отношению к внутреннему блоку. Если глобально описанный объект используется во внутреннем блоке, то на него распространяется внешнее (глобальное) описание.

В программе N0D1 переменные М, N, К являются локальными внутри процедуры; переменные А, В, С — глобальные. Однако внутри процедуры переменные А, В, С не используются. Связь между внешним блоком и процедурой осуществляется через параметры.

В программе N0D2 все переменные являются глобальными. В процедуре Evklid нет ни одной локальной переменной (нет и параметров). Переменные М и N, используемые в процедуре, получают свои значения через оператор присваивания в основном блоке программы и изменяют значения в подпрограмме. Результат получается в глобальной переменной К, значение которой выводится на экран. Здесь обмен значениями между основной программой и процедурой производится через глобальные переменные.

Использование механизма передачи через параметры делает процедуру более универсальной, независимой от основной программы. Однако в некоторых случаях оказывается удобнее использовать передачу через глобальные переменные. Чаще такое бывает с процедурами, работающими с большими объемами информации. В этой ситуации глобальное взаимодействие экономит память компьютера.

Функции. Теперь выясним, что такое подпрограмма-функция. Обычно функция используется в том случае, когда результатом работы подпрограммы должна быть скалярная (простая) величина. Тип результата называется типом функции. Формат описания функции следующий:

Как и у процедуры, у функции в списке формальных параметров могут присутствовать параметры-переменные и параметры-значения. Всё это — аргументы функции. Параметры вообще могут отсутствовать, если аргументы передаются глобально.

Программа решения рассмотренной выше задачи с использованием функции будет выглядеть следующим образом:

Из примера видно, что тело функции отличается от тела процедуры только тем, что в функции результат присваивается идентификатору функции: Evklid:=M.

Обращение к функции является операндом в выражении. Оно записывается в следующей форме:

Правила соответствия между формальными и фактическими параметрами все те же. Сравнивая приведенные выше программы, можно сделать вывод, что программа N0D3 имеет определенные преимущества перед другими. Функция позволяет получить результат путем выполнения одного оператора присваивания. Здесь также иллюстрируется возможность того, что фактическим аргументом при обращении к функции может быть эта же функция.

По правилам стандарта Паскаля, возврат в вызывающую программу из подпрограммы происходит, когда выполнение подпрограммы доходит до ее конца (последний End). Однако в современных версиях Паскаля есть средство, позволяющее выйти из подпрограммы в любом ее месте. Это оператор-процедура Exit. Например, функцию определения большего из двух данных вещественных чисел можно описать так:

Модифицированный алгоритм Евклида. Подпрограмму алгоритма Евклида можно составить иначе, если воспользоваться операцией mod (получение остатка от деления), имеющейся в Паскале. Идея алгоритма исходит из справедливости следующих равенств:

В таком случае функцию Evklid можно переписать так:

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 2.3. Конструирование алгоритмов

Информатика. 9 класса. Босова Л.Л. Оглавление

Ключевые слова:

Последовательное построение алгоритма

Существуют различные методы конструирования (разработки, построения) алгоритмов. Мы познакомимся с одним из них — методом последовательного построения (уточнения) алгоритма. Иначе он называется методом разработки «сверху вниз», нисходящим методом или методом пошаговой детализации.

Процесс последовательного построения алгоритма выглядит следующим образом.

На первом шаге мы считаем, что перед нами совершенный исполнитель, который «всё знает и всё умеет». Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в виде единого предписания — постановки задачи (рис. 2.2).

Если исполнитель не обучен исполнять заданное предписание, то необходимо представить это предписание в виде совокупности более простых предписании (команд). Для этого:

Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.

Объединяя полученные предписания в единую совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.

Разработка алгоритма методом последовательного уточнения для исполнителя Робот

Вы уже знакомы с исполнителем Робот. Он действует на клетчатом поле, между клетками которого могут быть стены.

Система команд исполнителя Робот:

В одном условии можно использовать несколько команд, применяя логические операций И, ИЛИ, НЕ.

Известно, что Робот находится где-то в горизонтальном коридоре. Ни одна из клеток коридора не закрашена.

Составим алгоритм, под управлением которого Робот закрасит все клетки этого коридора и вернётся в исходное положение.

Представим план действий Робота следующими укрупнёнными шагами (модулями):

Детализируем каждый из пяти модулей.

1. Чтобы закрасить все клетки коридора, находящиеся левее Робота, прикажем Роботу шагнуть влево и выполнить цикл-ПОКА:

Под управлением этого алгоритма Робот закрасит все клетки коридора, находящиеся левее от него, и окажется на клетке рядом с левой границей коридора.

2. Командой вправо вернём Робота в коридор. Наша задача — вернуть Робота в исходную точку. Эта точка имеет единственный отличительный признак — она не закрашена. Поэтому пока занимаемая Роботом клетка оказывается закрашенной, будем перемещать его вправо.

Под управлением этого алгоритма Робот окажется в исходной клетке.

4. Так как, выполнив предыдущий алгоритм, Робот оказался правее коридора, командой влево вернём его в коридор. Возвращение в исходную точку обеспечивается алгоритмом:

5. По команде закрасить Робот закрашивает исходную клетку.

Полностью программа управления Роботом выглядит так:

Вспомогательные алгоритмы

При построении новых алгоритмов нередко возникают ситуации, когда в разных местах алгоритма необходимо выполдение одной и той же последовательности шагов обработки данных. Для такой последовательности шагов создают отдельный алгоритм, называемый вспомогательным. В качестве вспомогательных могут использоваться алгоритмы, ранее разработанные для решения других задач.

Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.

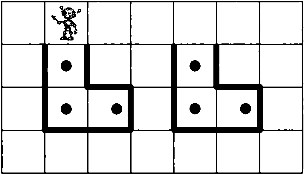
Пример 1. В среде КуМир составим алгоритм для исполнителя Робот, под управлением которого он нарисует узор:

Начальное положение Робота отмечено звёздочкой. В алгоритме использован вспомогательный алгоритм фигура.

При представлении алгоритмов с помощью блок-схем для обозначения команды вызова вспомогательного алгоритма используется блок «предопределённый процесс» (рис. 2.3), внутри которого записывается название (имя) вспомогательного алгоритма, после которого в скобках перечисляются параметры — входные данные и результаты.

Вспомогательный алгоритм делает структуру алгоритма более понятной.

Пример 2.

В приведённой записи дважды фигурирует вычисление степени с натуральным показателем. Поэтому в алгоритм вычисления степени с целым показателем можно включить вызов вспомогательного алгоритма вычисления степени с натуральным показателем. Соответствующая блок-схема:

Алгоритм, представленный на блок-схеме, является основным по отношению к вызываемому в нём вспомогательному алгоритму.

Параметрами используемого вспомогательного алгоритма являются величины а, n, у. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.

Команда вызова вспомогательного алгоритма исполняется следующим образом (рис. 2.4):

Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.

Рассмотрим несколько примеров рекурсивных алгоритмов.

Пример 3. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа а можно представить в виде рекурсивного:

n-я степень числа а есть не что иное, как произведение а n-1 • а; в свою очередь, а n-1 = а n-2 • а и т. д.

Пример 4. Рекурсивный алгоритм положен в основу эффективно го решения головоломки «Ханойская башня».

Пример 5. Рассмотрим алгоритм построения геометрической фигуры, которая называется снежинкой Коха. Шаг процедуры построения состоит в замене средней трети каждого из имеющихся отрезков двумя новыми такой же длины, как показано на рисунке:

С каждым шагом фигура становится всё причудливее. Граница снежинки Коха — положение кривой после выполнения бесконечного числа шагов.

Попробуйте подсчитать, сколько рёбер в границе снежинки Коха после четвёртого шага; после пятого шага.

САМОЕ ГЛАВНОЕ

Один из основных методов конструирования алгоритмов — метод последовательного построения алгоритма. Его суть состоит в том, что: исходная задача разбивается на несколько частей, каждая из которых проще всей задачи, и решение каждой части формулируется в отдельной команде; если получаются команды, выходящие за пределы возможностей исполнителя, то они представляются в виде совокупности ещё более простых предписаний. Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.Вспомогательный алгоритм — алгоритм, целиком используемый в составе другого алгоритма.Алгоритм, в котором прямо или косвенно содержится ссылка на него же как на вспомогательный алгоритм, называют рекурсивным.

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?

Источник