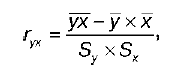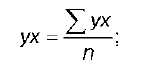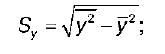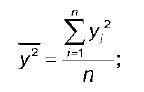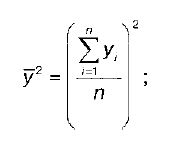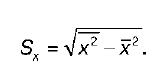Что такое выборочный коэффициент корреляции
Выборочный коэффициент корреляции



Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx.
Выборочный коэффициент корреляции является оценкой коэффициента корреляции Pxy генеральной совокупности.
Выборочный парный коэффициент корреляции ryx:
где ух – среднее арифметическое произведения факторной и результативной переменных:
у 2 – среднее значение из квадратов значений результативной переменной у :
y2 – квадрат средних значений результативной переменной у :
S x – выборочное среднеквадратическое отклонение факторной переменной х, показывающее, на сколько единиц в среднем отклоняются значения факторной переменной х от ее среднего значения x :
Выборочный коэффициент корреляции обладает следующими свойствами:
1) по абсолютной величине выборочный коэффициент корреляции не превосходит единицы: | r yx | ≤ 1, или –1 ≤ ryx ≤ 1;
2) если ryx = 0, т. е. выборочный коэффициент корреляции равен нулю, то переменные Y и Х не связаны статистической зависимостью. В этом случае проведение регрессионного анализа между исследуемыми переменными считается нецелесообразным;
3) если |ryx| = 1, т. е. выборочный коэффициент корреляции по абсолютной величине равен единице, то наблюдаемые значения исследуемых переменных связаны линейной функциональной зависимостью;
4) `если выборочный коэффициент корреляции принадлежит интервалу от нуля до единицы, то связь между исследуемыми переменными прямая; если же выборочный коэффициент корреляции принадлежит интервалу от нуля до минус единицы, то связь между исследуемыми переменными обратная.
Линейный коэффициент корреляции Пирсона
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.
Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.
Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.
Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т.к. является относительным показателем и не имеет единиц измерения.
Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r 2 = 0,01 или 1%, при r = 0,5 r 2 = 0,25 или 25%.
Выборочный коэффициент корреляции
Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.
Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.
В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:
Распределение z для тех же r имеет следующий вид.
Намного ближе к нормальному. Стандартная ошибка z равна:
Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.
Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:
Это была теоретическая часть. Переходим к практике расчетов.
Как посчитать коэффициент корреляции в Excel
Корреляционный анализ в Excel лучше начинать с визуализации.
На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.
Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.
Расчет доверительного интервала для коэффициента корреляции в Excel
В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:
— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.
Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.
Стандартная ошибка z легко подсчитывается с помощью формулы.
Используя функцию НОРМ.СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.
Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.
Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.
Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.
Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.
Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.
Несколько важных замечаний
1. Коэффициент корреляции Пирсона чувствителен к выбросам. Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).
2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.
3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.
В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.
Статистика. Ответы на экзаменационные билеты (10 стр.)
24. Выборочный коэффициент корреляции
Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx.
Выборочный коэффициент корреляции является оценкой коэффициента корреляции Pxy генеральной совокупности.
Выборочный парный коэффициент корреляции ryx:
у 2 – среднее значение из квадратов значений результативной переменной у :
y2 – квадрат средних значений результативной переменной у :
S x – выборочное среднеквадратическое отклонение факторной переменной х, показывающее, на сколько единиц в среднем отклоняются значения факторной переменной х от ее среднего значения x :
Выборочный коэффициент корреляции обладает следующими свойствами:
1) по абсолютной величине выборочный коэффициент корреляции не превосходит единицы: | r yx | ≤ 1, или –1 ≤ ryx ≤ 1;
2) если ryx = 0, т. е. выборочный коэффициент корреляции равен нулю, то переменные Y и Х не связаны статистической зависимостью. В этом случае проведение регрессионного анализа между исследуемыми переменными считается нецелесообразным;
3) если |ryx| = 1, т. е. выборочный коэффициент корреляции по абсолютной величине равен единице, то наблюдаемые значения исследуемых переменных связаны линейной функциональной зависимостью;
4) `если выборочный коэффициент корреляции принадлежит интервалу от нуля до единицы, то связь между исследуемыми переменными прямая; если же выборочный коэффициент корреляции принадлежит интервалу от нуля до минус единицы, то связь между исследуемыми переменными обратная.
25. Выборочное корреляционное отношение. Свойства выборочного корреляционного отношения
Выборочное корреляционное отношение является основным показателем при оценке тесноты нелинейной корреляционной связи между двумя переменными Y и Х. При изучении зависимости переменной Y от переменной Х выборочное корреляционное отношение обозначается как ηyx.
При изучении зависимости переменной Х от переменной Y выборочное корреляционное отношение обозначается как ηxy.
Выборочным корреляционным отношением
Y к Х называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Y:
где Gмежгр – это межгрупповое среднее квадратическое отклонение переменной Y:
G общ – это общее среднее квадратическое отклонение переменной Y:
где n – объем выборки (сумма всех частот);
m х – частота значениях переменной X;
m – частота значения у переменной Y;
у – среднее значение переменной Y;
у х – условная средняя переменной Y.
Выборочным корреляционным отношением X
к Y называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению переменной Х:
Выборочное корреляционное отношение обладает следующими свойствами:
1) значение выборочного корреляционного отношения принадлежит интервалу от нуля до единицы включительно:
2) если η yx = 0, т. е. значение выборочного корреляционного отношения равно нулю, то между исследуемыми переменными Y и Х корреляционная зависимость отсутствует;
3) если η yx = 1, т. е. значение выборочного корреляционного отношения равно единице, то между исследуемыми переменными Y и Х существует функциональная зависимость;
4) выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции:
5) если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, т. е. если
то между исследуемыми переменными существует точная линейная корреляционная зависимость. Основным достоинством выборочного корреляционного отношения η yx по сравнению с выборочным коэффициентом корреляции r yx является то, что показатель выборочного корреляционного отношения можно использовать как меру тесноты любой формы связи.
26. Общая модель парной регрессии
Предположим, что в результате статистического наблюдения были получены данные, характеризующие две переменные – Х и Y. С помощью корреляционного анализа было доказано наличие взаимосвязи между данными переменными. Следующим этапом исследования является задача определения точного вида выявленной зависимости между переменными с помощью регрессионного анализа.
Регрессионный анализ – это определение аналитического выражения связи или вида функции, в которой изменение одной величины (результативной переменной) обусловлено влиянием независимой величины (факторной переменной). Регрессионное уравнение, или регрессионная функция, количественно характеризует данную взаимосвязь.
Базисная регрессионная модель – это модель парной, или однофакторной, регрессии, в которой участвуют одна факторная и одна результативная переменные. Модель однофакторной регрессии называется полиномом первой степени и используется для описания равномерно развивающихся во времени процессов.
Модель парной регрессии зависимости результативной переменной у от факторной переменной х в общем виде записывается следующим образом:
где yi – значения результативной переменной, /= 1 ,n;
в 0, в 1 – неизвестные параметры модели парной регрессии;
n – количество наблюдений.
Модель парной регрессии зависимости результативной переменной х от факторной переменной у в общем виде записывается следующим образом:
Параметр ε i модели парной регрессии называется случайной ошибкой модели. Появление случайной ошибки в модели регрессии обусловлено следующими объективными предпосылками:
1) существованием вероятности того, что переменные, участвующие в модели, могут быть измерены с ошибкой.
2) включение в модель парной регрессии только одной факторной переменной, которая не способна полностью объяснить вариацию результативной переменной.
1. Путем визуальной оценки характера связи. На линейном графике по оси абсцисс откладываются значения факторной переменной х, по оси ординат – значения результативной переменной у. На пересечении соответствующих значений отмечаются точки. Полученный точечный график в указанной системе координат называется корреляционным полем. Если соединить полученные точки, то полученная линия будет называться эмпирической.
2. Путем теоретического и логического анализа природы изучаемых явлений, их социально-экономической сущности.