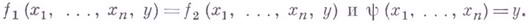Что такое вычислимая функция
Лекция 3. Вычислимые функции
Теория вычислимых функции разрабатывалась А. Чёрчем, и целью ее построения являлось получение точного (формального) определения понятия «алгоритм».
Для того, чтобы дать точное понятие алгоритма, необходимо определить, как задаются данные, с которыми будет работать Исполнитель, и как задаются элементарные шаги, из которых состоит алгоритм.
Универсальный способ представления различных данных – это представление их словами в некотором конечном алфавите. Действительно:
· если объект число, его можно представить в десятичной или двоичной форме, т. е. цепочкой символов алфавита <0,1>, или алфавита <0..9>.
· если объект – программа, то она является цепочкой символов в алфавите, содержащем буквы, цифры и специальные символы.
· если объект – изображение, то он представляется массивом пикселов, а каждый пиксел – тремя числами (интенсивностями красного, зеленого и синего цветов), т. е. изображение так же может быть закодировано строкой символов.
· современные высококачественные системы цифровой записи звука показывают, что и этот объект может быть адекватно описан строкой символов.
Таким образом, можно считать, что алгоритм – это преобразование слов из заданного алфавита в результирующее слово. Каким бы ни был конечный алфавит, любой его символ может быть закодирован с помощью двоичного алфавита. Иначе говоря, входные данные алгоритма могут быть представлены конечной цепочкой битов. То же самое можно сказать и о выходных данных. Каждая цепочка битов может интерпретироваться как целое неотрицательное число. Из этого можно сделать важный вывод: любому алгоритму может быть поставлена в соответствие некоторая функция, отображающая множество неотрицательных целых чисел в себя. Однако мы не утверждаем обратного. Существуют функции, не вычисляемые ни каким алгоритмом.
Вычислимой называют функцию, вычисляемую некоторым алгоритмом.
Вычислимая функция определяется на множестве целых неотрицательных чисел, результат функции так же должен принадлежать множеству целых неотрицательных чисел.
Итак, вычислимая функция – функция, для которой можно построить некоторый алгоритм. Алгоритм дает процедуру отыскания значений вычислимой функции. Но как отличить вычислимую функцию от невычислимой? Можно ли традиционным математическим языком описать общий вид вычислимых функций? А, написав, навести некоторый порядок среди алгоритмов, точнее ввести некий канонический вид написания алгоритмов, соответствующий строению вычислимых функций (мы помним, что для одной функции можно написать бесконечно много эквивалентных алгоритмов).
Для того чтобы внести ясность в эту проблему, поступим следующим образом.
1. Возьмем несколько простых базовых функций, для которых очевидно, что они могут быть вычислены, например, с помощью машины Тьюринга и составим из них набор Р.
2. Введем операции над функциями. Операции получают сами функции (а не значения функций) в качестве операндов и дают в результате новые функции. Эти операции так же должны быть очевидны с математической точки зрения, т. е. не должно возникать сомнений в том, что из вычислимых функций с помощью этих операций получаются вновь вычислимые функции. Обозначим набор этих операций О.
3. Произведем (мысленно) все возможные операции набора О над базовыми функциями набора Р, при этом будем по-разному комбинировать их в качестве аргументов. Все новые полученные функции включим в набор P и вновь произведем все возможные операции из набора О, подставляя в виде аргументов и по-разному комбинируя все возможные функции из уже расширенного набора P. Полученные при этом новые функции, так же включим в P и т. д.
При этом мы не ограничиваем сверху количество исполнений п.3., то таким образом будем получать все новые и новые функции. Иначе говоря, пп.1-3 описывают построение некоторого бесконечного множества функций. Однако, необходимо отметить, что каждая конкретная функция f из этого множества является результатом выполнения конечного числа операций, взятых из набора О над базовыми функциями.
Таким образом, процесс построения одной конкретной функции f:
1) начинается с исходных данных, выбираемых из базового набора;
2) выполняется пошагово (в дискретном времени);
3) на каждом шаге выполняется одна из элементарных операций (из набора О);
4) результат каждого шага строго определен;
5) процесс заканчивается через конечное число шагов.
Этот перечень дает нам возможность говорить об алгоритме αf построения функции f.
Заметим, что мы не вносим саму функцию f в перечень исходных данных, т. е. не говорим об универсальном алгоритме построения функции. Напротив, для различных функций f1 и f2 алгоритмы будут различны. Более того, свойство массовости алгоритмов не выполняется, т. к. исходные данные всегда одни и те же – базовый набор функций. Это позволяет говорить о том, что текст алгоритма (последовательность применения операций из О и места подстановок в эти операции операндов из базового набора) задает единственную функцию, а не множество функций. Таким образом, универсальный алгоритм, который на основе базовой функции построил бы любую функцию не существует.
С другой стороны, легко преобразовать алгоритм αf построения функции в алгоритм вычисления значений функции f(x1,x2,…,xn) введением и использованием в тексте исходных данных x1,x2,…,xn.
Введем сейчас конкретные базовый набор функций P и систему операций О для формирования множества функций. В качестве области определения функций возьмем n-кратное декартово произведение множества неотрицательных целых чисел. Сами функции, как и их аргументы также принимают значения из множества неотрицательных целых чисел. Таким образом, мы обеспечиваем возможность, хотя бы потенциальную, вычислять значения функций, с помощью рассмотренных ранее машин Тьюринга.
Базовый набор функций.
P=<Z(x), S(x), 
Z(x)=0, S(x) = x+1, 
Для этих функций не представляет труда построить машины Тьюринга, вычисляющие их значения по значениям аргументов. Покажем это.
1. Вычисление функции S(x)=x+1, увеличение аргумента на единицу. Используем алфавит A*=<0, 1, e>, причем x, будем кодировать последовательностью нулей и единиц, так как это принято в двоичном кодировании целых неотрицательных чисел. В момент старта головка машины Тьюринга находится напротив крайней левой ячейки с символом 1. В момент окончания работы головка машины Тьюринга так же должна находиться в крайнем левом положении (напротив крайней левой ячейки с символовом 1).
ВЫЧИСЛИМАЯ ФУНКЦИЯ
Общая идея различных подходов к созданию строгих математич. определений рассматриваемых понятий такова: проводится детальный анализ уже известных или мыслимых вычислительных процессов, выявляются существенные особенности этих процессов, находятся подходящие математич. аналоги этих процессов и их особенностей.
Реализация различных аспектов этой идеи неоднозначна и приводит к разным вариантам мате-матич. понятия алгоритма. Основными математич. моделями понятия алгоритма являются машины Тьюринга, частично рекурсивные функции, нормальные алгоритмы Маркова и др.
конечного алфавита 
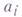

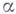

конечного списка 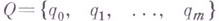

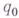
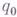
программы, составленной из отдельных команд 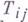

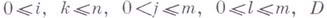
если D = Л, то получается слово 
если D=С, то получается слово
если D = П и В = a р В’, то получается слово
Работа машины Мможет быть описана следующим образом: кодируют исходные данные с помощью нек-рой начальной конфигурации (здесь 
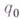
суперпозиция функций: если 

получается из 


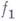

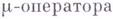
если 


Ясно, что если эти операции применяются к функциям, значение к-рых мы умеем вычислять, то имеются алгоритмы, вычисляющие значения функций 



Имеются легкие алгоритмы, вычисляющие значения простейших функций.
Нормальные алгорифмы Маркова. Всякий конкретный алгоритм имеет дело с нек-рым алфавитом, и решение конкретной задачи сводится к переработке слов данного алфавита по нек-рым заранее заданным правилам. Такой подход к теории алгоритмов развит А. А. Марковым, предложившим концепцию нормального алгорифма в качестве математич. модели понятия вычислительной процедуры.
Нормальный алгорифм j состоит из нек-рого алфавита 


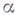

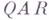
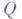



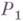
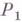
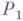
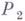
Кодируя соответствующим образом информацию, можно использовать нормальные алгорифмы для решения разнообразных алгоритмич. задач. Всякая вычислительная процедура, промоделированная с помощью нормального алгорифма, является эффективной в интуитивном смысле.
Обращение этого высказывания носит название тезиса Маркова: всякая эффективная вычислительная процедура может быть промоделирована с помощью подходящего нормального алгорифма. Если моделировать с помощью нормальных алгорифмов вычисление значений функций из класса F, то приходят к еще одному понятию вычислимой функции. Были предложены и другие уточнения понятия алгоритмов (см. Алгоритм, а также Нормальный алгорифм).
Доказан следующий результат о равносильности различных концепций понятия алгоритма: классы функций, вычислимых на машинах Тьюринга, частично рекурсивных функций, вычислимых с помощью нормальных алгорифмов Маркова (аналогичные классы функций при других концепциях понятия алгоритма), совпадают. По мнению большинства современных математиков, этот класс функций адекватен классу интуитивно В. ф. и отождествляется с ним. Такое 1 отождествление позволяет придать математичность алгоритмическим проблемам.
Лит.:[1] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [2] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972; [3] Тuring A. M., «Ргос. London Math. Soc.», 1937, v. 42, № 2, p. 230-65; [4] Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [5] Марков А. А., Теория алгорифмов, М., 1954 («Тр. матем. ин-та АН СССР», т. 42).
И. А. Лавров, А. Д. Тайманов.
Вычислимость, разрешимость и перечислимость
Вычислимые функции
Несколько замечаний по поводу этого определения:
Входами и выходами алгоритмов могут быть не только натуральные числа, но и двоичные строки (слова в алфавите <0,1>), пары натуральных чисел, конечные последовательности слов и вообще любые, как говорят, » конструктивные объекты «. Поэтому аналогичным образом можно определить понятие, скажем, вычислимой функции с двумя натуральными аргументами, значениями которой являются рациональные числа.
Несколько десятилетий назад понятие алгоритма требовало специального разъяснения. Сейчас (» компьютерная грамотность «?) такие объяснения все равно никто читать не будет, поскольку и так ясно, что такое алгоритм. Но все же надо соблюдать осторожность, чтобы не принять за алгоритм то, что им не является. Вот пример неверного рассуждения:
Разрешимые множества
Другими словами, X разрешимо, если его характеристическая функция 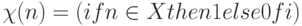
Аналогично определяют разрешимость множеств пар натуральных чисел, множеств рациональных чисел и т.п.
Перечислимые множества
Такой алгоритм не имеет входа; напечатав несколько чисел, он может надолго задуматься и следующее число напечатать после большого перерыва (а может вообще больше никогда ничего не напечатать тогда множество будет конечным).
Чтобы доказать эквивалентность этих определений, воспользуемся возможностью пошагового исполнения алгоритма.
Еще одно эквивалентное определение перечислимого множества : множество натуральных чисел перечислимо, если оно либо пусто, либо есть множество значений всюду определенной вычислимой функции (другими словами, его элементы можно расположить в вычислимую последовательность).
Теорема 1. Пересечение и объединение перечислимых множеств перечислимы.
4. Проведите это рассуждение, используя какое-либо другое эквивалентное определение перечислимости.
Как мы увидим, дополнение перечислимого множества не обязано быть перечислимым.
5. Иногда говорят о так называемых » недетерминированных алгоритмах » (оксюморон, но распространенный) такой алгоритм включает в себя команды типа
(достаточно, впрочем, команды » n := 0 или 1 «, так как произвольное число можно формировать по битам). Недетерминированный алгоритм (при одном и том же входе) может действовать по-разному, в зависимости от того, какие » произвольные » числа будут выбраны. Докажите, что перечислимое множество можно эквивалентно определить как множество чисел, которые могут появиться на выходе недетерминированного алгоритма (при фиксированном входе).
6. Докажите, что если множества 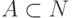
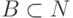
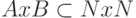
Содержание
Определение
Характеристики вычислимых функций
Основная характеристика вычислимой функции состоит в том, что должна существовать конечная процедура ( алгоритм ), указывающая, как вычислить функцию. Перечисленные выше модели вычислений дают разные интерпретации того, что такое процедура и как она используется, но эти интерпретации имеют много общих свойств. Тот факт, что эти модели предоставляют эквивалентные классы вычислимых функций, проистекает из того факта, что каждая модель способна читать и имитировать процедуру для любой из других моделей, так же как компилятор может читать инструкции на одном компьютерном языке и выдавать инструкции на другой язык.
Эндертон [1977] дает следующие характеристики процедуры вычисления вычислимой функции; аналогичные характеристики были даны Тьюрингом [1936], Роджерсом [1967] и другими.
Далее Эндертон перечисляет несколько пояснений этих трех требований процедуры для вычислимой функции:
Подводя итог, можно сказать, что на основе этого представления функция является вычислимой, если: (а) учитывая входные данные из своей области, возможно, полагаясь на неограниченное пространство хранения, она может дать соответствующий результат, следуя процедуре (программе, алгоритму), которая формируется конечное количество точных однозначных инструкций; (б) он возвращает такой результат (остановки) за конечное число шагов; и (c) если задан ввод, который не входит в его домен, он либо никогда не останавливается, либо застревает.
Область вычислительной сложности изучает функции с заданными границами времени и / или пространства, допустимыми для успешного вычисления.
Вычислимые множества и отношения
Поскольку каждое конечное отношение натуральных чисел может быть отождествлено с соответствующим набором конечных последовательностей натуральных чисел, понятия вычислимого отношения и вычислимо перечислимого отношения могут быть определены из их аналогов для множеств.
Формальные языки
Примеры
Вычислимы следующие функции:
Следующие примеры показывают, что функция может быть вычислимой, хотя неизвестно, какой алгоритм ее вычисляет.
Тезис Черча – Тьюринга
Тезис Черча – Тьюринга иногда используется в доказательствах, чтобы обосновать вычислимость конкретной функции, давая конкретное описание процедуры вычисления. Это разрешено, потому что считается, что все подобные случаи использования тезиса могут быть устранены утомительным процессом написания формальной процедуры для функции в некоторой модели вычислений.
Доказуемость
Множество доказуемо полных функций рекурсивно перечислимо : можно перечислить все доказуемо полные функции, перечислив все соответствующие им доказательства, которые доказывают их вычислимость. Это можно сделать, перечислив все доказательства системы доказательств и игнорируя не относящиеся к делу.
Связь с рекурсивно определенными функциями
Одной из таких функций, которая является доказуемой полной, но не примитивно рекурсивной, является функция Аккермана : поскольку она определена рекурсивно, действительно легко доказать ее вычислимость (однако аналогичный аргумент диагонализации также может быть построен для всех функций, определенных рекурсивным определением; таким образом, существуют доказуемые общие функции, которые не могут быть определены рекурсивно).
Всего функций, которые не являются доказуемо итоговыми
В звуковой системе доказательства каждая доказуемо полная функция действительно является полной, но обратное неверно: в каждой достаточно сильной и надежной системе доказательства первого порядка (включая арифметику Пеано) можно доказать (в другой системе доказательства), что существование полных функций, которые не могут быть доказаны в системе доказательств.
Невычислимые функции и неразрешимые проблемы
Каждая вычислимая функция имеет конечную процедуру, дающую явные и недвусмысленные инструкции по ее вычислению. Кроме того, эта процедура должна быть закодирована в конечном алфавите, используемом вычислительной моделью, поэтому существует только счетное количество вычислимых функций. Например, функции могут быть закодированы с использованием строки битов (алфавит Σ = <0, 1 >).
Расширения вычислимости
Относительная вычислимость
Высшая теория рекурсии
Гипервычисление
Хотя тезис Черча – Тьюринга утверждает, что вычислимые функции включают в себя все функции с алгоритмами, можно рассматривать более широкие классы функций, которые ослабляют требования, которым должны соответствовать алгоритмы. Область гиперкомпьютеров изучает модели вычислений, выходящие за рамки обычных вычислений Тьюринга.