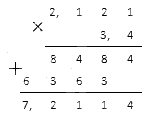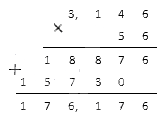Что такое вычислить рациональным способом
Рациональные приёмы вычислений на уроках математики
Разделы: Математика
Класс: 4
Ключевые слова: математика
«Мозг хорошо устроенный ценится больше,
чем мозг хорошо наполненный.»
Умения рационально производить вычисления характеризуют довольно высокий уровень математического развития. Знакомство и применение рациональных способов вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Эти умения чрезвычайно сложны, формируются они медленно и за время обучения в начальной школе далеко не у всех детей могут быть достаточно сформированы.
Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро. Считать в уме можно только при большом желании и систематической тренировки. И тогда перед вами откроется совсем другая математика: живая, полезная, понятная.
Скажите, пожалуйста, как рациональнее сложить 1+ 7, 4 * 8? Какие законы применили?
27 + 46+13? 27 – 19 – 7? Какие свойства, законы? Т.е основы рациональных приёмов вычислений основаны на чём?
Методика преподавания математики в начальных классах раскрывает основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами.
Рациональные приёмы сложения основываются
1. Коммуникативный закон сложения а +в =в +а
2. Ассоциативный закон сложения а+в+с = а+ (в+с)
на коммуникативном и ассоциативном приёмах сложения, а так же свойствах изменения суммы. Рассмотрим некоторые из них.
Свойства сложения.
а+в+с =У, то (а – к) +с+в = У –к
а+в+с=У, то (а+ к) +в +с = У+к
38 + 24+15 = 77, то 40+ 24 + 15 =?
Какие ещё рациональные приёмы сложения можно применить на уроке математики?
Округление одного из слагаемых; поразрядного сложения; приём группировки вокруг одного и того же «корневого» числа.
Рассмотрим эти приёмы:
13 + 49 + 76 + 61 = (поразрядное сложение)
38 + 59 = 38 + (…округление слагаемого)
26 + 24 + 23 +25 + 24 = (группировка вокруг одного и того же «корневого» числа
Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания.
Если уменьшаемое увеличить или уменьшить на число, то соответственно разность увеличится или уменьшится на это же самое число
74 – 28 = 46, то 77 – 28 = 49
74 – 28 = 46, то 71 – 28 = 43
Если вычитаемое увеличить или уменьшить на несколько единиц, то разность измениться в противоположную сторону.
Если уменьшаемое и вычитаемое уменьшить или увеличить на одно и тоже число, то разность не измениться.
Найди верные равенства.
229 – 36 = (229 – 9 ) – ( 36 – 6)
174 – 58 = (174 – 4) – ( 58 – 4)
358 – 39 = ( 358 – 8 ) – (39 – 8)
617 – 48 = ( 617 – 7 ) – (48 – 8)
Для рациональных вычислений используют частичные приёмы умножения и деления.
Приём замены множителя или делителя на произведение.
75 * 8 = 75 * 2*2*2=
960 : 15 = 960 : 3 : 5 =
Приём умножения на 9, 99,999, 11 …
87 * 99 = 87 * 100- 87 = 8700 – 87 = 8613
87 * 11 = 87 *10 + 87 = 870+ 87 = 957
Успешное применение различных приёмов зависит от умения подмечать особенности чисел и их сочетаний. Например, познакомив детей в первом классе с натуральным рядом чисел и имея его перед глазами, легко закрепить состав числа.
0 1 2 3 4 5 6 7
Отработав, таким образом, состав чисел в пределах 10 и познакомившись с переместительным законом сложения, дети легко справляются с заданием найти сумму чисел в пределах 10, а в дальнейшем, используя переместительное и сочетательное свойство сложения, легко можно найти сумму других чисел. Например:
Существуют приёмы на знаниях некоторых свойств чисел или результатов действий. Легко находить сумму последовательных нечётных чисел, начиная с 1.
Она равна произведению количества слагаемых на самого себя. (проверить)
Рационализация может осуществляться за счет возможности выполнять некоторые арифметические действия. Для этого очень важно научить детей внимательно рассматривать условия задания, суметь подметить все его особенности. Такие задания, как поставь нужный знак действия16 … 17 = 33 ( рассуждать), далее подобные задания усложняются. 8…6…33 = 15
Сравни, не вычисляя
51 : 3 … 30 : 3 + 21 :5
636 :6 … 600 : 6+ 30 : 6+ 6 :6
Используй рациональные приёмы вычисления, разгадай слово
Какие приёмы использовали?
Важно показать ученикам красоту и изящество устных вычислений, используя разнообразные вычислительные приёмы, помогающие значительно облегчить процесс вычисления.
СЧЁТ НА ПАЛЬЦАХ: способ быстрого умножения чисел первого десятка на 9. Допустим нам надо умножить 7 на 9. Повернём ладошки к себе, загнём седьмой палец, число пальцев слева от загнутого пальца – это число десятков, а число – справа, количество единиц.
Все задания, которые рассматривались, воспитывают интерес к математике, развивают их математические способности. Такую работу можно продолжать на математическом кружке.
Действия с рациональными числами: правила, примеры, решения
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .
Сложение противоположных рациональных чисел
Сумма противоположных чисел равна нулю.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Решение
Осуществим сложение дробей с разными знаменателями:
6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Решение
Сложение отрицательных рациональных чисел
Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Решение
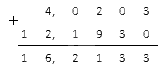
Действие вычитания рациональных чисел
При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Решение
Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7
Решение
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Произведение любого рационального числа a на нуль есть нуль.
Умножение на единицу
Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.
Умножение взаимообратных чисел
К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Решение
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Решение
Перемножим десятичные дроби столбиком:
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Решение
Умножение отрицательных рациональных чисел
Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Перемножим их столбиком:
Полученный результат и будет являться искомым произведением.
Деление рациональных чисел
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Решение
Рациональные способы вычислений
Описание презентации по отдельным слайдам:
Описание слайда:
Формирование вычислительных навыков.
Рациональные способы вычислений.
Автор: Карпенко Л.П.
Учитель школы 175
г.Зеленогорск
9.01.2009г.
Автор: Карпенко Л.П.,
учитель школы 175
г.Зеленогорск
9.01.2009г.
Описание слайда:
Что мы знаем о способах?
способы
позволяют
решать
быстрее
проще
легче
какие
!
!
где
применять
при
решении
примеров
при
решении
уравнений
при
устном
счете
2
Описание слайда:
Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительных навыков, основу которых составляет осознанное и прочное усвоение приёмов устных и письменных вычислений.
Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, являясь фундаментом изучения математики и других учебных дисциплин. Её основы закладываются в начальной школе.
правильность
рациональность
обобщённость
автоматизм
прочность
осознанность
Характеристики вычислительного навыка:
3
Описание слайда:
Остановимся более подробно на таком качестве вычислительного навыка как рациональность, которая напрямую связана с вариативностью.
Рациональность вычислений – это выбор тех вычислительных операций из возможных. «выполнение которых легче других и быстрее приводит к результату арифметического действия».
Знакомство с рационализацией вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Применение свойств арифметических действий позволяет учителю воспитывать интерес к математике, вызвать у детей желание научиться вычислять наиболее быстрыми и удобными способами. Такой подход позволит поддерживать стремление к использованию математических знаний в повседневной жизни.
Описание слайда:
Рациональные способы вычислений
«-»
3х498-498х2=
«+»
2х8+2х752=
ахb+aхc=aх(b+c)
«+»
(250+25)х4=
«-»
9х(70-2)=
способы
1.Сочетальное
св-во умн
2х(50х364)=
2.Сочетательное
св-во сложения
14+(16+307)=
3,4.Вынесение общего
множителя за скобку
5,6.раскрытие
скобок
7.Представление
суммы в виде
произведения
47+47+47+47=47х4
8.св-во вычитания
суммы из числа
798-(498+16)=
9.св-во вычитания
числа из суммы
(658+27)-58=
5
Описание слайда:
Счётное пособие –абак.
Описание слайда:
Учись считать с помощью простой линейки или полосок с числами двигая их относительно друг друга.
7
Описание слайда:
Таблица сложения и вычитания.
Таблица
умножения и деления.
8
Описание слайда:
Табличное деление и умножение
9
Описание слайда:
Совершенствование навыков устных вычислений зависит не только от методики организации урока, но и во многом от того, насколько дети проявляют интерес к предложенным знаниям. Этот интерес можно вызвать и разнообразными учебными пособиями:
На уроках математики, по теме «Сложение однозначных чисел с переходами через десяток», старые счеты превратила в практическое пособие для детей (на толстую проволоку поместила 10 косточек одного цвета и 10 другого. Дети четко видят десяток.
9
+
6
10
+
5
=
15
-1
9+1=10
+5 = 15
10
Описание слайда:
Мы сами составили таблицу таким образом, что включили в неё все случаи, где ответ (сумма) будет двузначным числом. Сделали заготовку для ответов (заготовили место для каждой из двух цифр).
Описание слайда:
После практической деятельности по прибавлению к 9 любого однозначного числа, дети пришли к выводу: «Чтобы к 9 прибавить любое однозначное число достаточно от этого числа отнять 1 и к полученному десятку прибавить остаток».
Важно, что ребенок сам осознал, что в ответе число единиц получается на один меньше того числа, которое прибавляешь. Дети испытывают радость открытия, общения друг с другом, радость взаимопонимания.
Новый прием развивает воображение, логическое мышление, умение рассуждать.
Этот же принцип действует при сложении 8,7,6 с любым однозначным числом.
На этом пособии удобно прийти к выводу о вычитании из любого двузначного числа (меньше 20)- 9,8,7,6.
Описание слайда:
Описание слайда:
3)Дети усматривают связь между произведениями: число десятков от произведения к произведению увеличивается на единицу, в то время как число единиц уменьшается:
10 9 х 4 = 36
Описание слайда:
Описание слайда:
Описание слайда:
Устные приёмы умножения.
Чтобы любое число умножить на 5,достаточно разделить его на 2 и умножить на 10 (т.к. 5-половина 10)
124 х 5 = 124 : 2 х 10 = 620
Чтобы умножить на 50,достаточно число разделить на 2 и умножить на 100 (т.к 50 –половина 100).
36 х 50 = 36 : 2 х 100 = 1800
Чтобы умножить на 25, достаточно число разделить на 4 и умножить на 100 (т.к. 25- четвёртая часть от 100) или наоборот. Если в остатке получится1, то вместо двух нулей поставим 25, если в остатке 2, то – 50,если 3, то – 75.
14 х 25 = 14 : 4 = 3(ост.2), значит 300 + 50 = 350
Чтобы умножить на 125, достаточно число разделить на 8 и умножить на1000(т.к. 125 – восьмая часть от1000)
48 х 125 = 48 : 8 х 1000 = 6000
17
Описание слайда:
Описание слайда:
68 х 99 = 68 х (100 – 1) =68 х 100 – 68 = 6800 – 68 = 6732
47 х 999 = 47 х (1000 – 1) = 47 х 1000 – 47=47000 – 47 = 46953
Но ещё проще ознакомить детей с правилом – « чтобы умножить число на 9 (99, 999) достаточно вычесть из этого числа число его десятков (сотен, тысяч), увеличенное на единицу, и к полученной разности приписать дополнение его цифры единиц до 10 (дополнение до 100 (1000) числа, образованного двумя (тремя) последними цифрами этого числа):
154 х 9 = (154 – 16) х 10 + (10 – 4) = 138 х 10 + 6 = 1380 + 6 = 1386
Умножение на 9, 99, 999
Чтобы умножить число на 9,( 99, 999)достаточно умножить его на 10 (100, 1000) и отнять это же число.
57 х 9 = 57 х 10 – 57 = 570 – 57 = 513
Описание слайда:
Интересно, что 7 х 11 х 13 = 1001 (число Шехерезады)
7 х 143 = 1001
11 х 91 = 1001
77 х 13 = 1001
Описание слайда:
Описание слайда:
Для малых чисел: число справа налево делят по 2 цифры и складывают. Если сумма делится на11, то всё число делится.
528 5 + 28 =33, значит делится.
: на12 числа, которые делятся и на 4, и на 3.
: на14 числа, которые делятся и на 7, и на 2.
: на 15 числа, которые делятся и на 3, и на 5.
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Приём замены множителя разностью
Приём замены множителя произведением:
35 х 6= 35 х ( 2 х 3) = (35 х 2) х 3 = 70 х 3 = 210
125 х 48 = 125 х (8 х 6) = ( 125 х 8) х 6 = 1000 х 6 = 6000
26
Описание слайда:
Описание слайда:
Описание слайда:
3)При увеличении ( уменьшении) уменьшаемого и вычитаемого на несколько единиц разность не изменяется:
231 – 96 = (231 + 4) – (96 +4) = 235 – 100 = 135
3. Умножение.
При увеличении ( уменьшении) одного из множителей на несколько единиц умножаем полученное целое число и прибавленные (отнятые) единицы на другой множитель и из первого произведения вычитаем второе произведение (полученные произведения складываем).
97 х 6 = (100 – 3 ) х 6 = 100 х 6 – 3 х 6 = 600 – 18 = 582
29
Описание слайда:
Некоторые способы вычислений могут показаться сложными, но при правильной организации работы на уроке и внеклассных занятиях учащиеся осваивают их и с удовольствием используют в вычислительной деятельности. Привычка выполнять подобные вычисления устно формирует устойчивый навык, который не раз сыграет добрую службу при изучении более сложного материала.
Вариативность вычислительных навыков учащихся формирует интерес, положительную мотивацию к вычислительной деятельности, даёт возможность знакомить школьников с известными вычислительными секретами, показать практическую значимость математики, тогда перед детьми откроется совсем другая математика – живая, полезная и понятная.
30
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Приёмы рациональных вычислений.
Одно из самых важных умений человека – это умение быстро и правильно выполнять вычисления.
Рационализация вычислений означает выполнение вычислений более лёгким, более целесообразным способом.
Устные вычисления способствуют активизации мыслительной деятельности, развитию логического мышления, сообразительности, памяти, творческих начал и волевых
качеств. Способность к умственному (устному) счёту полезна
в отношении практическом и, как средство, для здоровой умственной гимнастики.
1. Приём, основанный на использовании свойств
арифметических действий.
· 89 + 67 + 11 = 89 + 11 + 67 = 167
· 357 + 996 + 48 = 357 + 996 + (43 + 4 + 1) =
= (357 + 43) + (996 + 4) + 1 = 400 + 1000 +1 = 1401
· 25 × 37 × 4 = 37 × (25 × 4) = 37 × 100 =3700
· 87 × 4 + 4 × 13 = (87 + 13) × 4 = 100 × 4 = 400
· 367 : 5 – 167 : 5 = ( 367 – 167) : 5 = 200 : 5 = 40
2. Приём округления.
· 399 + 473 = 400 +472 = 872
· 497 + 196 + 299 = 492 + 200 + 300 = 992
· 196 + 199 + 197 = 200 × 3 – 8 = 592
· 752 – 298 = 754 – 300 = 454
· 134 + 27 + 29 + 38 = 150 + 20 + 30 + 37 = 200 + 37 = 237
· 427 + 28 + 7 + 20 + 652 = 430 + 649 + 30 + 5 + 20 =
= 1079 + 1 + 54 = 1080 + 20 + 34 = 1134
· 198 × 3 = (200 – 2) × 3 = 600 – 6 = 594
· 35 × 18 = 35 × (20 – 2) = 700 – 70 = 630
3. Приём, основанный на зависимости результата от
изменения компонентов действий.
· 56 – 38 = 60 – 42 = 18
· 225 : 75 = (225 2) : (75 2) = 450 : 150 = 3
· 440 : 55 = 880 : 110 = 8
· 364 : 6 + 118 : 3 = 364 : 6 + 236 : 6 = (364 + 236) : 6 = 600 : 6 = 100
4. Приёмы последовательного умножения и деления.
· 75 × 8 = 75 × 2 × 2 × 2 = 150 × 2 × 2 = 300 × 2 = 600
· 35 × 18 = 35 × 2 × 9 = 70 × 9 = 630
· 23 × 55 = 23 × (5 × 11) = 115 × 11 = 1150 + 115 = 1 265
· 540 : 4 = (540 : 2) : 2 = 270 : 2 = 135
· 960 : 15 = (960 : 3) : 5 = 320 : 5 = 64
5. Приёмы умножения и деления на 5, 50, 500, 25, 250, 15, 125.
· 36 × 5 = (36 : 2) × 10 = 180
· 826 × 50 = (826 : 2) × 100 = 41 300
· 84 × 25 = (84 : 4) × 100 = 2 100
· 24 × 15 = 12 × 30 = 360
· 496 × 125 = (496 : 8) × 1000 = 62 000
· 4 340 : 5 = (4 340 : 10) × 2 = 868
· 4 000 : 125 = (4 000 × 8) : (125 × 8) = 32 000 : 1 000 = 32
6. Приёмы умножения на 9, 99, 11, 101. 1001.
· 26 × 9 = 25 × (10 – 1) = 250 – 25 = 225
· 35 × 99 = 3 500 – 35 = 3 465
· 37 × 11 = 37 × (10 + 1) = 370 + 37 = 407
· 73 × 101 = 7 300 + 73 = 7 373
· 735 × 1 001 = 735 000 + 735 = 735 735
Так, наблюдая и выявляя свойства чисел и действий над
ними, ученики накапливают сведения и используют их затем при
вычислениях. Овладение некоторыми приёмами рациональных
вычислений готовит детей к успешному изучению математики в
Вычислите наиболее рациональным способом
Добрый вечер!
Мне даны такие примеры: 1) 1,17 + 11,2 + 1,83 + 10,8; 2) 5,21 − 3,3 − 4,7 + 6,79; 3) 4,21 + 16,5 + 3,89 + 4,4. Вычислите наиболее рациональным способом значение этих примеров. Я то решить их могу, но как это сделать наиболее рациональным способом понятия не имею и вообще для чего это делается не знаю!
Доброй ночи! Да, я согласна, что у вас возникло недоумении в решении данных пример, да ещё и с таким условием: вычислите наиболее рациональным способом.
Ну что ж. Единое, чем могу обрадовать, то вы спокойно можете решать так, как и решали, вычитать и прибавлять. От этого, по сути, ничего не изменится, кроме вашего времени.
Вот именно поэтому детей учат, как это рациональней делать, чтоб экономить своё время. В их случае — при решении контрольных, а в случае со взрослыми людьми, даже если они не связаны с математикой, или тем, где присутствует счёт., — при каждодневных расчётах в тех же магазинах, либо же при подсчёте стоимости коммунальных услуг. То есть, этому есть практическое применение и тема появилась далеко не случайно.
В чём же суть рационального способа. Так в том, что мы выполняем действия над числами так, чтоб они по возможности складывались или отнимались легче, получая десяток, либо до десятка, чтоб точно не потерять какую=то единичку, двоечку. Давайте попробуем конкретно разобраться на предоставленных примерах.
Вот таким образом и происходит группирование членов примера для того, чтоб вычислить их наиболее рациональным способом.
надеюсь, Вам это поможет при решении подобных заданий, с таким условием. Но если такого условия нет, то можете делать, как хотите. Главное, — чтоб результат был правильным!
Успехов Вам!
Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.